Математические термины и символы история возникновения и развития: История математических обозначений — Википедия – Проект » История происхождения математических знаков»

«Из истории происхождение математических знаков»

Подготовила: ученица 7г Мынэскуртэ Анастасия

Цифры – первые математические знаки

Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад.

ПРОИСХОЖДЕНИЕ МАТЕМАТИЧЕСКИХ ЗНАКОВ

Сколько раз, складывая, вычитая, умножая и деля, вы использовали математические знаки: «+», «-», «^.», «:». Задумывались ли вы о том, откуда они пришли к нам и что изначально обозначали?

Одно из объяснений происхождения знака «+» таково. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» (и) приходилось писать очень часто, то его стали сокращать: писали одну букву t, которая в конце концов и превратилась в знак «+».

Однако «приобретение» особых знаков для обозначения арифметических действий нельзя полностью приписывать только европейским математикам. Еще древние египтяне обозначали сложение специальным знаком – рисунком шагающих ног.

Для обозначения вычитания в III в. до н. э. в Греции использовали знак – перевернутую греческую букву «пси» (ψ). Итальянские математики использовали для этого букву m (μ), начальную букву слова «минус». В XVI в. для обозначения действия вычитания стали применять знак «–» и, чтобы отличать минус от тире, Л.Ф. Магницкий (XVIII в.) стал обозначать вычитание знаком «–».

Для обозначения действия умножения некоторые европейские математики XVI в. употребляли букву М – начальную букву латинского слова, обозначавшего увеличение, умножение, — multiplicatio (мультипликация). В XVII в. некоторые математики стали обозначать умножение косым крестиком «х», а другие употребляли для этого точку. В конце XVIII в. большинство математиков стало употреблять для обозначения умножения точку, однако допускали и употребление косого креста.

Действие деления не обозначали знаком на протяжении тысячелетий. Его просто называли и записывали словами. Индийские математики стали первыми обозначать деление начальной буквой названия этого действия – D. Арабы ввели для обозначения деления черту. Ее перенял от арабов в XVIII в. итальянский математик Фибоначчи (Леонардо Пизанский). Знак двоеточия «:» для обозначения деления вошел в употребление в конце XVII в. До этого у некоторых математиков встречался знак «–», которым они обозначали это действие.

Знак равенства обозначали в разные времена по-разному: и словами, и разными символами. Знак «=», столь удобный и понятный в настоящее время, стали широко использовать только в XVIII в. А предложил его для обозначения равенства двух выражений автор учебника алгебры англичанин Роберт Рикорд в 1557 г. Он так объяснил свой выбор: «Никакие два предмета не могут в большей степени быть равны между собой, как две параллельные прямые».

Знак «=» стал общепризнанным благодаря Г.В. Лейбницу.

Обыкновенная дробь

Привычная нам «двухэтажная» запись обыкновенной дроби использовалась ещё древнегреческими математиками, хотя знаменатель у них записывался над числителем, а черты дроби не было. Индийские математики переместили числитель наверх; через арабов этот формат переняли в Европе. Дробную черту впервые в Европе ввёл Леонардо Пизанский (1202)

но в обиход она вошла только

при поддержке Иоганна Видмана (1489).

Знак % закрепился для обозначения процентов в XVII веке. Вероятно, он произошел от сокращения латинского слова «centum» в «cto«. При скорописи «cto» стало выглядеть как «о/о», а затем — «%».

Было очень неудобно хранить хрупкие и тяжелые глиняные таблички, веревки с узелками, рулоны папируса. И это продолжалось до тех пор, пока древние индийцы не изобрели для каждой цифры свой знак.

Предки русского народа – славяне — для обозначения чисел также употребляли буквы

Материал к урокам математики «Из истории математических терминов»

ИЗ ИСТОРИИ МАТЕМАТИЧЕСКИХ ТЕРМИНОВ

От этого же корня происходит наше слово линолеум, первоначально означавшее льняное полотно.

Мы привыкли к тому, что бубен имеет круглую форму , но раньше бубны имели форму квадрата или ромба , о чем свидетельствуют изображения «бубен» на игральных картах.

От этого же слова происходит наше слово « трапеза», означающее стол.

Слово ДИАГОНАЛЬ происходит от греческого « диа», что означает «через» и « гония» — угол, т.е. рассекающая углы, проходящая через углы.

ЦИЛИНДР происходит от латинского слова «цилиндрус», означающего «валик», «каток».

Пирамида – латинская форма греческого слова «пюрамис», которым греки называли египетские пирамиды; это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне.

Рассмотрим истоки слова и термина «пирамида». Сразу стоит отметить что «пирамида» или “pyramid” (английский), “piramide” (французский, испанский и славянские языки), “pyramide” (немецкий) — это западный термин, берущий свой исток в древней Греции. В древнегреческом πύραμίς («пирамис» и мн. ч. πύραμίδες «пирамидес») имеет несколько значений. Древние греки именовали «пирамис» пшеничный пирог, который напоминал форму египетских сооружений. Позже это слово стало означать «монументальную структуру с квадратной площадью в основании и с наклонными сторонам, встречающимися на вершине». Происхождение греческого слова πύραμίς имеет собственную историю. По одной из версий греки заимствовали это слово из Египта, где есть схожее по звучанию “Pir E Mit” , означающее «часть числа» или «составляющая часть совершенства», но не пирамиду, как сооружение. Этимологический словарь указывает, что греческое «пирамис» происходит из египетского “pimar”.

Из греческого слово перешло в латинский язык и вплоть до 16 века не трансформировалось в европейских языках, поскольку в средневековой Европе о пирамидах в Египте знали лишь образованные люди, говорящие на латыни. Первое письменное толкование слова «пирамида» встречается в Европе в 1555 г. и означает: «один из видов древних сооружений королей». После открытия пирамид в Мексике и с развитием наук в 18 веке, пирамида стала не просто древним памятников архитектуры, но и правильной геометрической фигурой с четырьмя симметричными сторонами (1716 г.).

Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.

Корень – (квадратный или корень уравнения) пришло от арабов. Арабские ученые представляли себе квадрат числа, вырастающий из корня – как растение, и потому называли корнями.

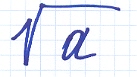
Алгоритм. В IX в. ал-Хорезми изложил позиционную систему в сочинении «Об индийском числе». Латинский перевод этого труда начинался словами: «Dixit Algorithmi», — сказал ал-Хорезми». Отсюда и произошел термин «алгоритм» («алгорифм»). В средневековой Европе слово означало всю систему десятичной позиционной арифметики.

Современное понятие алгоритма установилось в середине 30-х годов XX в. в работах Геделя, Чёрча, Тьюринга, Поста, А.А. Маркова. Алгоритм — точное формальное предписание, однозначно определяющее содержание и последовательность операций, переводящих заданную совокупность исходных данных в искомый результат.

В начальной школе простейшими алгоритмами являются правила, по которым выполняются сложение, вычитание, умножение, деление.

Алгебра. Математическая наука, объектом изучения которой являются алгебраические системы, например группы, кольца, поля и др. Отдельной ветвью алгебры является элементарная алгебра.

Первый учебник алгебры — «Краткая книга об исчислении ал-Джабра и ал-Мукабалы» был написан в 825 г. арабским ученым ал-Хорезми. Слово ал-джабр при этом означало операцию переноса вычитаемых из одной части в другую и его буквальный смысл — «восполнение». Этот термин стал названием науки. В Европе такое название употреблялось уже в самом начале XIII в., но еще Ньютон называл алгебру «Общей арифметикой» (1707). Книга ал-Хорезми имеет особое значение в истории математики как руководство, по которому долгое время обучалась вся Европа. Именно под влиянием арабской математики алгебра сформировалась как учение о решении уравнений.

Слово «хорда» происходит от греческого слова «хорде» — «кишка», «струна» (в древней Греции струны выделывались из воловьих кишок). И в Древней Греции, и в александрийской школе это слово не связывалось с хордой. И Евклид, и Птолемей, и другие александрийские ученые называли хорду «прямой в круге», имея в виду прямолинейный отрезок, вписанный в круг (треугольник, вписанный в круг, они также называли «треугольником в круге»).

Аксиома. Термин впервые встречается у Аристотеля и перешел в математику от философов древней Греции. В переводе с греческого слово означает «достоинство», «уважение», «авторитет». Первоначально термин имел смысл «самоочевидная истина».

В современном понимании аксиома — высказывание некоторой теории, принимаемое при построении этой теории без доказательства, т.е. принимаемое как исходное, отправное для доказательств других положений этой теории (теорем). Аксиомы называют также постулатами.

Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.

Происхождение термина «Геометрия», что буквально означает «землемерие», можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому (4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы». Уже у древних греков Геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, Геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах и т.п. Первоначальные понятия Геометрия возникли в результате отвлечения от всяких свойств и отношений тел, кроме взаимного расположения и величины. Первые выражаются в прикосновении или прилегании тел друг к другу, в том, что одно тело есть часть другого, в расположении «между», «внутри» и т.п. Вторые выражаются в понятиях «больше», «меньше», в понятии о равенстве тел.

Слово «синус» — латинского происхождения. Если мы посмотрим в латинско-русский словарь, мы увидим там такие значения этого слова: 1) изогнутость, кривизна, изгиб, выпуклость; 2) пазуха, карман, складка тоги (древнеримская одежда) на груди; 3) платье, одежда; 4) грудь, объятия; 5) нежная любовь, забота; 6) середина, центр; 7) убежище, прибежище; 8) залив, бухта; 9) впадина, углубление, провал. Слово «синус» хорошо известно врачам в значении «пазуха», «впадина». Однако ни одно из этих многочисленных значений не имеет никакого отношения к синусу в тригонометрии. Откуда же произошел этот термин?

Тригонометрия появилась впервые в I—II веках нашей эры в Александрии, в работах знаменитых александрийских астрономов, наиболее крупным из которых был Клавдий Птолемей. Однако в тригонометрии Птолемея основным понятием был не синус, а хорда. В книге Птолемея «Математическая система» были таблицы зависимости длин хорд от длин стягиваемых ими дуг, причем дуги измерялись в градусах, минутах и секундах, а хорды— в частях радиуса: здесь радиус считался равным 60 частям, хорды измерялись в этих долях радиуса, в их «минутах» (60-х долях) и в их «секундах» (60-х долях «минут»). Это «шестидесятеричное» деление дуг и хорд было заимствовано александрийскими астрономами у вавилонян.

НПК на тему «Тайны математических символов»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 19»

города Новочебоксарска Чувашской Республики

Научно-исследовательская работа

Тайны математических символов

Выполнила: ученица 5-в класса Баряева Дарья

Руководитель: учитель математики Филиппова Лариса Николаевна

Новочебоксарск-2015год

Содержание:

1.Введение

2.Математическте символы

1)Знаки сложения и вычитания

2)Знак равенства

3)Знаки умножения и деления

4)Знак процента

5)Знак бесконечности

6)Знаки угла и перпендикулярности

7)Знак параллельности

8) Число пи

9)Краткая запись «Что и требовалось доказать»

3.Заключение

4.Литература

5.Приложение

Введение

Проблема:

Ребята с первого класса знакомятся со многими математическими обозначениями. Становясь старше, они заинтересовываются о происхождении математических знаков, терминов. Наш проект приоткроет завесу некоторых из этих тайн.

Цель: Создать электронное пособие.

Задачи:
• собрать информацию по теме проекта
• систематизировать собранный материал
• создать презентацию

• познакомить учащихся 4-6 классов с познавательными фактами из истории математики

Актуальность проекта

Когда я училась в начальных классах, у меня даже не появлялось мысли о том, откуда взялся знак умножения или знак равенства, я просто выполняла задания учителя, не задумываясь о таких вещах. Так было до недавнего времени, пока я не познакомилась с обыкновенными дробями и не узнала от учителя о различном обозначении обыкновенных дробей. Я заинтересовалась этой проблемой, и у меня появилось множество вопросов. Я думаю, что у ребят помладше возникает их не меньше. Мой проект раскрывает некоторые тайны происхождения математических знаков, терминов. Разыскивая информацию, я сама узнала много интересного, думаю, это будет интересно и другим ребятам, а также их родителям и учителям. Желаю успеха!

Слово математика пришло к нам из древнегреческого, где μάθημα означало «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания.

Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.

Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.

С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.

С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.

Математические символы

1)Знаки сложения, вычитания

История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример — кость Ишанго. Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.

В Древнем Египте была уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в качестве символа сложения используется изображение двух ног, идущих вперед по тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полуэллиптическую кривую для вычитания.

Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.

Считается, так же, что наш знак 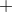происходит от одной из форм слова “et’’, которое по-латыни значит “и’’. Выражение a + b писалось на латыни так: a et b. Постепенно, из-за частого использования, от знака «et» осталось только » t » , которое, со временем превратилось в » + «. Первым человеком, который, возможно, использовал знак 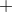как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века.

В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “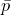’’ или “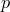’’ (обозначая “плюс’’) для сложения и “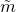’’ или “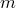’’ (обозначая “минус’’) для вычитания.

Обозначения вычитания были более запутанными, так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.

Первое использование современного алгебраического знака “” относится к немецкой рукописи по алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: « 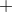» и « — » . Систематическое использование знаков « 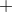» и « — » для сложения и вычитания встречается у Иоганна Видмана. Немецкий математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок присутствия и отсутствия студентов на своих лекциях. Правда, есть сведения, что он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака 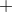и , в труде «Быстрый и приятный счёт для всех торговцев» (ок. 1490)

Как исторический курьез, стоит отметить, что даже после принятия знака 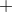не все использовали этот символ. Видман сам ввел его как греческий крест 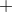(знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид « ».

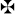2)Знак равенства

Знак равенства в математике и других точных науках пишут между двумя идентичными по своему размеру выражениями. Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный). В античной и средневековой математике равенство обозначалось словесно, например, est egale, или использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые буквы слова “равный’’, но это не было общепринятым. Знак равенства «=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde R., 1510-1558). Математическим символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя одинаковыми горизонтальными параллельными отрезками, гораздо более длинными, чем те, что используются сегодня. Английский математик Роберт Рекорд был первым, кто начал использовать символ «равенство», аргументируя словами: «никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». Но ещё в XVII веке Рене Декарт использовал аббревиатуру “ae’’. Франсуа Виет знаком равенства обозначал вычитание. Некоторое время распространению символа Рекорда мешало то обстоятельство, что такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. Распространение знак получил только после работ Лейбница на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда. На его могильной плите нет слов – просто вырезан знак «равно».

Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом

3) Знаки умножения и деления

Знак умножения в виде крестика («х») ввел англиканский священник-математик Уильям Отред в 1631 году. До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран, 1659).

Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).

Для обозначения действия деления Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. Деление в виде обелюс («÷») ввел швейцарский математик Иоганн Ран (ок. 1660)

4)Знак процента.

Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.

5)Знак бесконечности

Нынешний символ бесконечности «∞» ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного» (лат. Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque Difficiliora Matheseos Problemata), где ввёл придуманный им символ бесконечности. До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента) математиком Бернулли приблизительно сорок лет спустя.

Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение без конца. По линиям числа 8 можно совершать, как по велотреку, бесконечное движение. Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Получилось 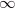. Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8.

Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.

Многие считают, что лист Мёбиуса является прародителем символа бесконечности, т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса

6) Знаки угла и перпендикулярности

Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ перпендикулярности у него был перевёрнут, напоминая букву T. Символ угла напоминал значок 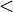, современную форму ему придал Уильям Отред (1657).

7) Знак параллельности

Символ «параллельности» известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey) и др. математики XVII века).

8) Число пи

Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια —окружность и περίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.

Синус и косинус

Интересно появление синуса и косинуса.

Sinus с латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в тригонометрии продвинулись индийские математики в районе 5 века. Самого слова «тригонометрия» не было, оно было введено Георгом Клюгелем в 1770 году.) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для краткости называли просто — джия (тетива). Когда арабы переводили работы индусов с санскрита, они не стали переводить «тетиву» на арабский, а просто транскрибировали слово арабскими буквами. Получилась джиба. Но так как в слоговой арабской письменности краткие гласные не обозначаются, то реально остается дж-б, что похоже на другое арабское слово — джайб (впадина, пазуха). Когда Герард Кремонский в 12 веке переводил арабов на латынь, он перевел это слово как sinus, что по-латыни также означает пазуху, углубление.

Косинус появился автоматически, т.к. индусы называли его коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука на санскрите. Современные краткие обозначения 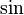и 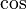введены Уильямом Отредом и закреплены в трудах Эйлера.

Обозначения тангенса/котангенса имеют намного более позднее происхождение (английское слово tangent происходит от латинского tangere — касаться). И даже до сих пор нет унифицированного обозначения — в одних странах чаще используется обозначение tan, в других — tg

9) Сокращение «Что и требовалось доказать» (ч.т.д.)

«Quod erat demonstrandum» (квол эрат лэмонстранлум).
Греческая фраза имеет значение «что требовалось доказывать», а латинская — «что нужно было показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого математика Древней Греции Эвклида (III в. до н. э.). В переводе с латинского — что и требовалось доказать. В средневековых научных трактатах эту формулу писали часто в сокращенном виде: QED.

Математические обозначения.

История символов

+ —

Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии.

× ∙

Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).

/ : ÷

Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века.

Знак равенства предложил Роберт Рекорд (1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем.

Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше.

Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно. Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше.

√

Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.

aⁿ

Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676).

( )

Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц.

Знак суммы ввёл Эйлер в 1755 году

Знак произведения ввёл Гаусс в 1812 году

Букву i как код мнимой единицы: 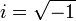предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).

Общепринятое обозначение числа 3.14159… образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр, то есть длина окружности.

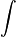
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa).

y’

Краткое обозначение производной штрихом восходит к Лагранжу.

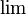
Символ предела появился в 1787 году у Симона Люилье (1750—1840).

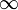
Символ бесконечности придумал Валлис, опубликован в 1655 году.

3. Заключение

Математическая наука необходима для цивилизованного общества. Математика содержится во всех науках. Математический язык смешивается с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий.

Литература

1.Что? Зачем? Почему? Большая книга вопросов и ответов. Пер.Мишиной К., А Зыковой -М: Издательство ЭКСМО, 2007

2. Глейзер Г.И. История математики в школе VII-VIII кл. Пособие для учителей. М: Просвещение, 1982

3. Рыбников К.А. История математики. Издательство Московского Университета, 1974

4. Интернет. www математические символы.

Приложение.

Копилка стихотворений.

Число пи

Гордый Рим трубил победу
Над твердыней Сиракуз,
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь.
Чтобы нам не ошибаться,
Чтоб окружность верно счесть.
Надо только постараться
И запомнить все, как есть:
Три-14-15-92 и шесть.
(п= 3,1415926)

Арифметические знаки

Как не на свете без ножек столов,
Как нет на свете без рожек козлов,
Котов без усов и без панцирей раков,
Так нет в арифметике действий без знаков!

«+»

Я добрый знак соединенья

И в том мое предназначенье

Я для сложения гожусь,

И этим очень я горжусь!

В математике есть знак.
Без него нельзя никак!
Он не жадный, но отнять
Может от восьмёрки пять.

«-»
Я – минус,
Тоже добрый знак.
Ведь не со зла я отнимаю,
Я свою роль лишь выполняю.

Из цифры вычтем мы другую,
Ставим черточку прямую.
Этот знак мы узнаем,
«Минус» мы его зовем.

Перед скобкой “минус” строгий
Загородит нам дорогу.
Чтобы скобки убирать,
Надо знаки поменять.

«*»

Его нам надо пригласить,

Чтоб разных чисел ряд сложить.

Для облегчения сложенья

Есть знак отличный – . . . (умноженье)

«:»

Не все в этом действии гладко:

То целиком, а то – с остатком.

В несколько раз уменьшение

Выполнит знак вам . . . (деление)

Ребусы

Этимология математических терминов | Социальная сеть работников образования

Название	Определение	С какого языка перевод	Что означает термин	Кто и когда ввёл
Арифметика	Раздел математики, занимающийся изучением свойств числа, вопросами происхождения и развития понятия «число», свойствами операций и отношений в числовых множествах, а также анализом аксиоматической структуры числовых множеств.	Греческий язык	«Аритмос» — «число», и «технэ» — «искусство». Буквально «числовое искусство»	В русский язык слово вошло в16 веке.
Абсцисса	Одна из декартовых координат точки, обычно первая, обозначаемая буквой х.	Латинский язык	«Абсцисса» — «отрезанная»	Немецкий учёный Лейбниц ввел понятия «абсцисса» в 1665 г.
Аксиома	Основное положение, принимающее без доказательства	Греческий язык	«Аксиома» — «принятие положения»	Впервые встречается у Аристотеля (384-322 д.н.э.)
Биссектриса	Прямая, проходящая через вершину угла и делящая его пополам.	Латинский язык	«Бис» – дважды и «секо» – секу. Буквально «рассекающая на две части»
Вектор	Направленный отрезок прямой, у которого один конец (точка А) называют началом вектора, другой конец (точка В ) – концом вектора.	Латинский язык	«Вектор» — «несущий», «носитель».	Ирландский учёный У. Гамильтон (около 1845)
Гипотенуза	Сторона прямоугольного треугольника, лежащая против прямого угла.	Греческий язык	«Гюпотейнуса» — «стягивающая».	Древнегреческий ученый Евклид (3 век до н.э.) вместо этого термина писал, “сторона, которая стягивает прямой угол”.
Геометрия	Часть математики, изучающая пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре.	Греческий язык	«Земля» и «метрео») – «измеряю». Буквально – «землемерие»
Градус	Единица измерения плоского угла, равная 1:90 части прямого угла.	Латинский язык	«Градус» — «шар», «ступень»
Диагональ	Отрезок прямой, соединяющий две его вершины, не лежащие на одной стороне	Греческий язык	«Диа» — «через» и «гониа» — «угол». Буквально « проходящая через угол»	Термин встречается у Евклида
Диаметр	Хорда, проходящая через её центр, равная удвоенному радиусу окружности.	Греческий язык	«Диаметрос» — «поперечник»	Был открыт Фалесом Милетским.
Дискриминант	а+bx+c где а,b, с – заданные числа, а х – произвольное число, — число D, равное – 4ас	Латинский язык	«Дискриминанс» — «разделяющий», «различающий».
Индекс	Числовой или буквенный указатель, которым снабжаются математические выражения для того, чтобы отличать их друг от друга.	Латинский язык	«Индекс» — «указатель»
Катет	Сторона прямоугольного треугольника, лежащая против острого угла.	Греческий язык	Катерос — «отвес».
Квадрат	Прямоугольник, у которого все стороны равны , или, что равносильно, ромб, у которого все углы равны.	Латинский язык	«Квадратус» – «четырёхугольный».
Координаты	Числа, заданием которых определяется положение точки на прямой, на плоскости или в пространстве, а также на кривой или поверхности.	Латинский язык	«Ко» — «совместно» и «ординатус» — «упорядоченный», «определённый».	Немецкий учёный Лейбниц ввел понятия «координата» — в 1692 г.
Коэффициент	Числовой множитель	Латинский язык	«Ко» — “с”, “вместе” и «эффиценс»- “производящий”, “составляющий причину чего либо”. Буквальное значение – “содействующий”.	Возник из выражения Виета “longitudo coefficiens”- “содействующая длина” (1591).
Куб	Один из пяти правильных многогранников, имеет 6 граней, 12 ребер и 8 вершин.	Греческий язык	«Кюбос» — «игральная кость»	Название введено пифагорейцами, затем термин встречается у Евклида.
Лемма	Вспомогательное предположение, употребляемое при доказательстве других утверждений	Греческий язык	«Лемма» — «допущение»	Древнегреческий учёный Архимед
Линия		Латинский язык	«линеа» — льняная (имеется в виду льняная нить).
Математика	Наука о количественных отношениях и пространственных формах действительного мира	Греческий язык	«Матема» — «знание», «наука»
Масштаб	Отношение длины линии на чертеже к длине соответствующей линии в натуре.	Немецкий язык	«Мас» — «мера» и «штаб» — «палка».
Минус	Знак (горизонтальная черта – ) для обозначения действий вычитания, а также для обозначения отрицательных чисел.	Латинский язык	«Минус» — «менее».	Первое употребление слова минус найдено в итальянской математике 14 века.
Медиана	Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.	Латинский язык	«Медианус» — «средний».
Нуль (ноль)	Число, обладающее тем свойством, что любое число при сложении с ним не меняется.	Латинский язык	«Нулюс» — «никакой»	Некоторые ученые предполагают, что нуль заимствован у греков. Другие полагают, что нуль пришел из Индии.
Ордината	Одна из декартовых координат очки, обычно вторая, обозначаемая буквой y.	Латинский язык	«Ординатум» — «по порядку», «расположенная в порядке».	Немецкий учёный Лейбниц ввел понятия «ордината» — в 1694 г.
Параметр	Величина, значения которой служат для различения элементов некоторого множества между собой.	Греческий язык	Параметрон — «отмеривающий».
Параллелограмм	Четырёхугольник, у которого противоположные стороны попарно параллельны.	Греческий язык	«Параллелос» — «параллельный», и «грамма» — «линия».	Евклид
Периметр	Сумма длин всех сторон многоугольника	Греческий язык	«Пери» — «вокруг», «около», «метрео» – «измеряю».	Архимед (3 в.до н.э.), Герон (1 в.н.э.), Паппа (3в.)
Перпендикуляр	Прямая, пересекающая данную прямую под прямым углом.	Латинский язык	«Перпендикулярис» — «отвесный»	Пришло через западноевропейские языки.
Планиметрия	Часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости.	Греческий язык	«Планум» — «плоскость» и «метрео» — «измеряю»
Плюс	Знак (+) для обозначения действия сложения, а также для обозначения положительных чисел.	Латинский язык	«Плюс» — «больше»	Первое употребление слова plus как обозначения действия сложения найдено историком математики Энестремом в итальянской алгебре 14 века. Чешский учёный Я. Видман (1489)
Пропорция	Равенство между двумя отношениями четырёх величин.	Латинский язык	«Пропорцио» — «соотношение», «соразмерность»	Современное определение впервые дал Цамберти, директор инженерной школы в Риме (15 век). Современную запись A:B=C:D ввел Лейбниц (1708).
Процент	Сотая доля целого числа, обозначаемая %.	Латинский язык	«Про» и «центум» — «за сто».
Радиус	Отрезок, соединяющий центр окружности с какой – либо её точкой, а также длина этого отрезка.	Латинский язык	«Радиус» — «спица колеса», «луч».	Французский учёный П.Раме (1569)
Ромб	Четырёхугольник, у которого все стороны равны.	Греческий язык	«Ромбос» — «бубен»	Герон (1 в.н.э.), Паппа (3в.)
Сумма	Результат сложения.	Латинский язык	«Сумма» — «итог», «общее количество»	Букву S ввел Эйлер в 1755 году.
Сегмент	Часть круга, ограниченная дугой m его граничной окружности и хордой, соединяющей концы этой дуги.	Латинский язык	«Сегментум» — «отрезок», «полоса».	греческий астроном Птолемей
Сектор	Часть круга, ограниченная дугой его граничной окружности и двумя её радиусами, соединяющими концы дуги с центром круга.	Латинский язык	«Секо» — «режу».	Евклид
Симметрия	Свойство формы или расположение фигур.	Греческий язык	«Симметриа» — «соразмерность».
Скаляр	Величина, каждое значение которой выражается одним числом.	Латинский язык	«Скалярис» — «ступенчатый».	Ирландский учёный У. Гамильтон (1843)
Точка		Латинский язык	“пункт” – пунктир; “пунктум” – укол, медицинский термин “пункция” – прокол
Трапеция	Четырёхугольник, у которого две противоположные стороны параллельные.	Греческий язык	«Трапедзион» — «столик».	Древнегреческий учёный Посидоний (в. до н.э.)
Тригонометрия	Раздел геометрии, в котором изучаются тригонометрические функции и их приложения к геометрии.	Греческий язык	«Тригонон» — «треугольник», «метрео» – «измеряю».	Немецкий учёный Б.Питиск (1595)
Фигура	Термин, применяемый к разнообразным множествам точек; обычно фигурами называют такие множества, которые можно представить состоящими из конечного числа точек.	Латинский язык	«Фигура» — «внешний вид», «образ».
Формула	Комбинация математических знаков, выражающая какое-либо правило	Латинский язык	«Формула» — «правило», «предписание»
Хорда	Отрезок, соединяющий две её точки.	Греческий язык	«Хорде» — «струна», «тетива».
Цифры	Условные знаки для обозначения чисел.	Латинский язык	«Цифра» — «нуль», «пустое место»	Индийские математики называли знак обозначавший отсутствие некоторого разряда словом “сунья” — пустой. Арабы перевели этот термин по смыслу и получили слово “сифр”.

Материал (алгебра) по теме: История математических терминов

ИСТОРИЯ МАТЕМАТИЧЕСКИХ ТЕРМИНОВ

«ЛИНИЯ» происходит от латинского слова «линеа» — льняная (имеется в виду льняная нить).

От этого же корня происходит наше слово линолеум, первоначально означавшее льняное полотно.

КВАДРАТ произошел от латинского слова «кваттуор» (четыре) — фигура с четырьмя сторонами.

РОМБ происходит от латинского слова «ромбус», означающего бубен.

ТРАПЕЦИЯ происходит от латинского слова «трапезиум» -столик.

От этого же слова происходит наше слово « трапеза», означающее стол.

Слово ДИАГОНАЛЬ происходит от греческого « диа», что означает «через» и « гония» — угол, т.е. рассекающая углы, проходящая через углы.

КОНУС – это латинская форма греческого слова «конос», что означает сосновую шишку.

ЦИЛИНДР происходит от латинского слова «цилиндрус», означающего «валик», «каток».

ПРИЗМА – латинская форма греческого слова «присма» — опиленная (имелось в виду опиленное бревно).

Пирамида – латинская форма греческого слова «пюрамис», которым греки называли египетские пирамиды; это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне.

СФЕРА – латинская форма греческого слова «сфайр» — мяч.

Точка – (лат. “пункт” – пунктир; “пунктум” – укол, медицинский термин “пункция” – прокол).

Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.

Корень – (квадратный или корень уравнения) пришло от арабов. Арабские ученые представляли себе квадрат числа, вырастающий из корня – как растение, и потому называли корнями.

Алгоритм. В IX в. ал-Хорезми изложил позиционную систему в сочинении «Об индийском числе». Латинский перевод этого труда начинался словами: «Dixit Algorithmi», — сказал ал-Хорезми». Отсюда и произошел термин «алгоритм» («алгорифм»). В средневековой Европе слово означало всю систему десятичной позиционной арифметики.

Алгебра. Математическая наука, объектом изучения которой являются алгебраические системы, например группы, кольца, поля и др. Отдельной ветвью алгебры является элементарная алгебра.

Слово «хорда» происходит от греческого слова «хорде» — «кишка», «струна» (в древней Греции струны выделывались из воловьих кишок). И в Древней Греции, и в александрийской школе это слово не связывалось с хордой. И Евклид, и Птолемей, и другие александрийские ученые называли хорду «прямой в круге», имея в виду прямолинейный отрезок, вписанный в круг (треугольник, вписанный в круг, они также называли «треугольником в круге»).

В современном понимании аксиома — высказывание некоторой теории, принимаемое при построении этой теории без доказательства, т.е. принимаемое как исходное, отправное для доказательств других положений этой теории (теорем). Аксиомы называют также постулатами.

Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.

Вторые выражаются в понятиях «больше», «меньше», в понятии о равенстве тел.

Слово «синус» — латинского происхождения. Если мы посмотрим в латинско-русский словарь, мы увидим там такие значения этого слова: 1) изогнутость, кривизна, изгиб, выпуклость; 2) пазуха, карман, складка тоги (древнеримская одежда) на груди; 3) платье, одежда; 4) грудь, объятия; 5) нежная любовь, забота; 6) середина, центр; 7) убежище, прибежище; 8) залив, бухта; 9) впадина, углубление, провал. Слово «синус» хорошо известно врачам в значении «пазуха», «впадина». Однако ни одно из этих многочисленных значений не имеет никакого отношения к синусу в тригонометрии. Откуда же произошел этот термин?

Формирование математической символики

Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Волгоградский государственный университет»

Реферат на тему:

Формирование математической символики

Выполнила: студентка группы ПМПОм-121

Шешукова Е. Г.

Волгоград 2013г.

Введение

Математика – первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число в виде нарисованных в ряд палочек. Можно сказать, что 1 палочка – это первый математический символ. Развитие математики началось примерно в 3000г. до н.э. благодаря вавилонянам и египтянам.

Источником знаний о вавилонской цивилизации служат хорошо сохранившиеся глиняные таблички, датируются от 2000г. до н.э. Математика на каменных табличках в основном была связана с ведением хозяйства. Арифметика использовалась при обмене денег и расчётах за товары, вычисление процентов, налогов и даже урожая. Геометрические задачи возникли в связи со строительством каналов, зернохранилищ и храмов. Очень важной задачей математики был расчёт календаря. Календарь использовался для сельскохозяйственных работ и религиозных праздников. Деление окружности на 360, а градуса на минуты берут начало в вавилонской астрономии. Вавилоняне составили таблицы для обратных чисел, таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней.

Наше знание древнеегипетской математики основано на двух папирусах 1700г до н.э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов, размеры податей, в строительстве и астрономии. Древнеегипетская письменность основывалась на иероглифах. Для каждого числа от 1 до 9 был свой иероглиф. А также для чисел 10, 100, 1000, 10000 и т.д.

А в Греции математики и философы принадлежали к высшим слоям общества, где любая практическая деятельность рассматривалось, как недостойное занятие. Математики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на арифметику – теоретический аспект и логистику – вычислительный аспект. Логистикой занимались низкие классы и рабы. Древние римляне изобрели систему исчисления, основанную на использовании букв для отображения цифр.

С открытием математических правил и теорем ученые придумывали новые математические обозначения. Система обозначения для любой области знания играет важную роль. Математические знаки служат в первую очередь для точной записи математических понятий и предложений в компактной форме. Система математических символов представляет собой универсальный язык. Использование символов позволяет формулировать законы или математические теории в общем виде.

Математические обозначения – это символы, используемые для компактной записи математических уравнений и формул. Помимо цифр и букв математический язык использует множество специальных символов, которые формировались в течение нескольких столетий.

История формирования математических символов

Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления.

Знаки сложения и вычитания ( +, — )

Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году (Рис. 1). До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии.

Рисунок 1. Первое появление знаков «плюс» и «минус». Страница из книги Иоганна Видмана.

Знаки умножения ( × , ∙ )

Первое определение действия умножения восходит к грекам. Знак умножения в виде косого крестика ввел Оутред 1631 год. Это обозначение принял Лейбниц. Во всеобщее употребление знак вошел благодаря «Основаниям всех наук» Вольфа 1710 год. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621). Знаки точка и «х» отобраны среди множества символов, придуманных различными авторами.

Знаки деления ( /, : , ÷ )

В математике древности не было деления — его производили последовательным вычитанием. До распространения современного способа деления эта операция была трудной и громоздкой. Термины деление, делимое, делитель появились сравнительно поздно у Герберта в конце X века, когда он был центральной фигурой у ученых.

Из современных знаков деления старейший — горизонтальная черточка, она была у Герона и Диофанта, затем встречается у Леонардо Пизанского. Однако во всеобщее употребление горизонтальная черта вошла лишь в XVI-XVII веке. Отред предпочитал косую черту. Двоеточие введено в «Арифметике» Джонса (1633 год). С 1684 года двоеточие как знак деления употребляет Лейбниц. Швейцарец Ран ввел знак двоеточие с чертой 1659 год. В 1923 году Национальный Комитет Математических Проблем постановил прекратить употребление этого знака.

Знак равенства ( = )

До появления специального знака слово «равенство» писали на разных языках, а затем «унифицировали» математический язык и в научный обиход вошло слово aequatura или сокращенно aequ. В 1557 году английский математик и врач Рекорд предложил знак =, «ибо, — писал он, — ничего нет более равного, чем две параллельные прямые». В континентальной Европе знак равенства был введён Лейбницем.

Знаки неравенств ( >, < , >>, << )

После введения знака равенства английский ученый Гарриот ввел в употребление знаки неравенства 1631 год. До него писали словами: больше, меньше. << и >> были введены Борелем и Пуанкаре 1901 год при сравнении рядов и впоследствии приобрели смысл «много мньше» и «много больше».

Символ процента (%)

Знак корня ( √ )

Древнегреческие математики говорили «найти сторону по данной площади квадрата» вместо извлечь корень. Следуя этой традиции, раньше квадратный корень называли «стороной». Знак корня ввел автор первого учебника по алгебре на немецком языке, учитель математики в Вене Рудольф (1525 год). Затем в 1637 году Декарт объединил знак корня с горизонтальной чертой — знаком скобок, и получился современный знак.

Возведение в степень (aⁿ)

Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676).

Логарифм ( log, lg, ln )

Логарифмы были изобретены Непером, шотландским бароном, и Бюрги, другом Кеплера, королевским придворным часовых дел мастером в Праге, а также мастером астрономических инстрементов. Непр изобрел логарифмы не позднее 1594 года. Непр не употреблял никаких символов для обозначения логарифмов.

Напрашивающиеся сокращения у Кеплера в 1624 году, Бриггса в 1631 году, Оутреда в 1647 году употреблялись в течение века без строго различия. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов.

Обозначения дроби

На всех языках дробь называется «ломаным, раздробленным числом». До эпохи Архимеда дроби описывали словами. Архимед и Диофант писали знаменатель над числителем, без черточки. Современная запись ведет начало от индусов, у которых ее переняли арабы: числитель пишется над знаменателем. Черту для их разделения впервые применил Леонардо Пизанский (1202 год). Потом эта запись исчезла и появилась вновь только у Видмана 1489 год. Запятую в десятичных дробях ввели итальянский астроном Маджини (1592 год) и Непер (1617 год).

Скобки ()

До появления специальных символов перед выражением, которое нужно было заключить в скобки, ставили слово collect и т.п. Знаки, выполняющие роль скобок появились в XV веке. Широкое применение скобки получили лишь в первой половине XVIII века благодаря Лейбницу и еще больше Эйлеру.

Термин интервал происходит от латинского intervallum — промежуток, расстояние. Современные обозначения появились впервые в 1909 году в книге немецкого профессора математики Г. Ковалевского.

Модуль ( | | )

Термин происходит от латинского modulus — мера. Широко использовался в математике. Модуль перехода (при логарифмировании) ввел Коутс. Модуль сравнения введен Гауссом в 1801 году. Слово всегда использовал Коши в теории комплексной переменной (начиная с 1829 года). Символ || появился у Вейерштрасса для комплексного числа довольно рано в 1841 году.

Знаки суммы и произведения ( Σ, П )

Знак суммы ввёл Эйлер в 1755 году. Знак произведения ввёл Гаусс в 1812 году.

Знак мнимой единицы ( i )

Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).

Обозначение числа ( π )

Интеграл ( ∫ )

В превой половине XVII века при вычислении фигуры операцию записывали словами: «совокупность всех неделимых». Лейбниц ради сокращения вводит начальную букву Summa, которая по начертанию того времени писалась как наш знак интеграла.

Обозначение производной ( y’ )

Краткое обозначение производной штрихом восходит к Лагранжу.

Обозначение дифференциала ( d )

Лейбниц для «бесконечно малой разности» использовал обозначение d — первую букву слова differential. Обозначени dx появилось у него в 1675 году.

Обозначение предела ( lim )

Символ предела появился в 1787 году у Симона Люилье (1750—1840).

Градиент

Термин происходит от латинского gradior — идти вперед. Символический вектор был введен ирландским ученым Гамильтоном в 1846 году (Рис. 2).

Рисунок 2. Градиент.

Параллельность

С греческого означает «рядом идущая». Слово стало употребляться как математический термин 2 500 лет назад в школе пифагора. Для обозначения использовался знак =

Лишь после введеного Рекордом знака равенства стали пользоваться знаком || (Керси 1637, Вильсон).

Синус, косинус, тангенс, котангенс

Слово встречается в индийских сидхантах — анонимном труде по астрономии IV или V век и в «Ариабхатиам» (сочинение по астрономии и математике Ариабхаты 476 год). Линия синуса называлась «ардхаджива»: «ардха» означает «половина», а «джива» — «тетива лука, хорда». Позднее синус стали сокращенно называть «джива». В IX веке было заменено арабским словом «джайб». При переводах на латынь переводчики Роберт Честерский(1145) и Герард Кремонский (1175) употребили слово sinus. Современное обозначение sin употребляли Симпсон, Эйлер, Кестнер, Д’Аламбер, Лагранж. Благодаря Эйлеру утвердились обозначения sin, cos, tg.

Термин «косинус» представляет собой сокращение выражения complementi sinus — т.е. «дополнительный синус». В трудах арабских математиков косинус рассматривается только как синус дополнения угла до 90 градусов. Этот термин как и «котангенс», ввел английский математик и астроном, Гентер в 1620 году. Благодаря Эйлеру эти обозначения стали общепринятыми.

Градус

Латинское слово gradus означает «шаг». Как заметили вавилонские жрецы, солнечный диск укладывается по дневному пути Солнца 180 раз, т.е. «Солнце делает 180 шагов». Тогда путь за сутки равен «360 шагам». Круг стали делить на 360 частей.

Обозначения, напоминающие современные, использовались Птолемеем, который употреблял шестидесятеричную систему исчисления. Он называл градусы «частями» и обозначал минуты штрихом, а секунды двумя штрихами (‘ и «)

Современные знаки ввел медик и математик Плетье (1558 год). Эти обозначения распространились очень быстро и к 1600 году стали общепринятыми.

Обозначение бесконечности ( ∞ )

Математики Греции пытались дать определение понятиям бесконечность, предел и столкнулись с непреодолимыми трудностями. Эти понятия были корректно определены только в XIX веке. Современное определение бесконечности предложил Дедекин в книге «Что такое числа и чем они должны быть», 1888.

Знак для указания неограниченного возрастания был введен Валлисом (1655). Предполагают, что Валлис использовал римский символ, означавший 1000. Знак стал общепринятым с XVIII века.

Заключение

Анри Пуанкаре писал: «В ее строго логической форме математическая дисциплина принимает столь искусственный характер, что ставит в тупик любого. Забывая исторические истоки, мы видим, как вопросы могут быть разрешены, но перестаем понимать как и почему они были поставлены».

Прежде чем понять, что означает какой либо математетический символ, необхадимо узнать историю появления этого символа.

Математическая наука необходима для цивилизованного общества. Математика содержится во всех науках. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий.

Проект по инновационной деятельности на тему: «Геометрические термины и символы».

Муниципальное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа №5 с углублённым изучением отдельных предметов городского округа Ступино Московской области

Проект по инновационной деятельности на тему:

«Геометрические термины и символы».

Выполнила: Быстрова Н.Н.

учитель математики

2018г.

Оглавление

Введение
Описание проектной работы и её результаты
Рефлексия деятельности
Приложение

Введение

«Предмет математики настолько серьёзен,

что полезно не упускать случая сделать его

немного занимательным».

Б. Паскаль.

История науки показывает, что логическая структура и рост каждой математической теории, начиная с определенного этапа ее развития, становятся все в большую зависимость от использования математической символики и ее усовершенствования.

Система математических терминов и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл. Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.

Тема символики была, есть и будет одной самых интригующих, интересных и актуальных тем. Наверное, нет ни одной науки, которая бы не использовала символику. Замечания Л. Карно, что в математике «символы не являются только записью мысли, средством ее изображения и закрепления, – нет, они воздействуют на самую мысль, ни, до известной степени, направляют ее, и бывает достаточно переместить их на бумаге, согласно известным очень простым правилам, для того, чтобы безошибочно достигнуть новых истин».

В чем заключено объективное содержание математической символики? Чем объясняется значение символики в математике?

Решающей силой развития математической символики является не «свободная воля» математиков, а требования практики математических исследований. Именно реальные математические исследования помогают математикам в конце концов выяснить, какая система знаков наилучшим образом отображает структуру рассматриваемых количественных отношений, в силу чего может быть эффективным орудием их дальнейшего изучения.

Описание проектной работы и её результаты

В целях выявления и поддержки одаренных и талантливых детей, расширения кругозора учащихся в области математики; формирования познавательных интересов и способностей, навыков исследовательской деятельности; развития мотивации обучающихся к познанию и творчеству; был проведён конкурс мультимедийных и проектных работ «Геометрические термины и символы» среди учащихся 9 «а» класса .

Свои работы предоставили – Бузунова Юлия, Моисеев Дмитрий, Миронов

Серафим. Ребятам захотелось рассказать о истории возникновения математических терминов и символов, получить расширенную информацию о терминах и символах, обозначающие геометрические фигуры и отношения между ними, о применении для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем. Проект опирается на предметы: математика, история. В ходе его участники создадут презентации, рефераты, содержащие материалы о терминах и символах, раскроют их смысл.

В процессе выполнения проекта обучающиеся получат новый взгляд на изучаемый геометрический материал:

осмыслят и многократно повторят основные математические термины;
научатся наглядно представлять изучаемый материал;
систематизируют исторический материал по теме.

В процессе реализации проекта учащиеся научатся:

подбирать необходимый для работы материал;
выдвигать гипотезы;
интерпретировать результаты исследования;
делать выводы;
работать в различных поисковых системах;
представлять результаты исследования в виде презентаций и докладов;
вести диалог, участвовать в дискуссии.

Рефлексия деятельности

Оценивание качества результатов

Изучение законов природы немыслимо без знаний математики. Не случайно известный итальянский физик и математик Галилей сказал так: «Природа говорит языком математики, буквы этого языка – круги, треугольники и иные математические знаки».

Данная проектная деятельность максимально способствует раскрытию творческого потенциала ребёнка, воспитывает индивидуально выраженную личность. У ребят получились хорошие проекты, и каждый из них раскрыл тему по своему, они постарались передать свой внутренний мир, внести своё я.

Приобретены поисково-исследовательские, творческие, коммуникативные умения, презентационные умения и навыки.

При создании данного проекта у учащихся формируются такие качества, как:

— умение планировать свою работу;
— умение самостоятельно генерировать идеи;
— умение запросить недостающую информацию у эксперта;
— умение самостоятельно найти недостающую информацию в информационном источнике;
— умение находить несколько вариантов решения проблемы;
— умение выдвигать гипотезы;
— умение отстаивать свою точку зрения;
— умение уверенно держать себя во время выступления;
— умение использовать различные средства наглядности при выступлении.

Приложение

В приложении представлены данные работы учащихся МБОУ «СОШ №5».