Правило 72. Когда удвоятся накопления?
20 май 2019 Сергей Кикевич Все авторы
Приложение к статье:файл для скачивания
Правило 72 – это отличный способ приближенно посчитать время, необходимое для удвоения капитала при известной доходности.
Разделив 72 на доходность инвестиций, мы получим примерное количество лет, через которое начальные инвестиции удвоятся:

Например, если инвестировать 1 рубль под 10%, то через 72/10 = 7,2 лет вложения удвоятся.
Правило 72 дает довольно точные результаты при низких ставках доходности. По мере роста доходности погрешность увеличивается.
Другие применения правила 72
Кроме расчета срока удвоения капитала правило 72 может успешно применяться и в других ситуациях.
Расчет ставки
Мы можем поинтересоваться, какая ставка нужна инвестору для того чтобы удвоить свои накопления за определенный срок.
- Для того чтобы удвоить капитал за 4 года необходимо инвестировать деньги под 18%
Удвоение ВВП
Правило 72 дает отличный пример того, как важен каждый процент роста ВВП (Внутренний валовый продукт).
- Для того чтобы ВВП России удвоился (сохранив текущие 2,3% годового роста) потребуется 31 год
- Если рост экономики снизится до 2%, для удвоения ВВП потребуется 36 лет
- Если рост экономики увеличится до 4%, для удвоения экономики нужно 18 лет
Инфляция и падение покупательной способности денег
Правило 72 отлично подходит для иллюстрации падения покупательной способности денег при известной инфляции.
- При инфляции 4,2% (данные Росстата за 2018 год) цены вырастут в два раза через 17 лет
- При инфляции 10% уже через 7,2 года вы сможете купить в магазине в 2 раза меньше за те же деньги
Стоит заметить, что 10,8% — это всё еще средняя инфляция в России за период с января 2000 года (19 лет).
Правило 72 может применяться универсально во всех ситуациях, где что-то растет с известной скоростью (например, рост населения).
Откуда взялось число 72?
По правилу сложного процента рост инвестиций рассчитывается следующим образом:

PV– начальные инвестиции
r – доходность
N– количество лет
FV– конечная сумма денег через N лет
Подробнее об этой формуле читайте в Формулы древних: чудеса сложного процента.
Итак, 1 рубль превратиться в 2 через N лет при доходности инвестиций r:


Берем натуральный логарифм обеих сторон уравнения:


Согласно приближенной формуле 



Погрешность формулы  сохраняется на относительно небольшом уровне даже для r = 25%. При более высоких темпах роста можно использовать следующий уровень приближения со вторым членом ряда Тейлора
сохраняется на относительно небольшом уровне даже для r = 25%. При более высоких темпах роста можно использовать следующий уровень приближения со вторым членом ряда Тейлора 
Правило легко можно было назвать правилом 69,3. Но для приближенных расчётов используют все-таки 72 из-за удобства. 72 – это число с большим количеством делителей: 2, 3, 4, 6, 8, 9 и 12.
У числа 70 количество делителей меньше, но его можно использовать для большей точности (оно ближе к 69,3).
Расчеты в EXCEL
В EXCEL существует универсальная формула КПЕР, которая рассчитывает количество периодов (лет или месяцев), необходимых для достижения цели.
Например, воспроизведем расчет с удвоением капитала при доходности 10% при помощи КПЕР:
=КПЕР(Доходность;0;Начальные инвестиции;Цель;1) = 7,27
Доходность = 10%
Начальные инвестиции = 1
Цель =2
КПЕР является гораздо более универсальным инструментом по сравнению с правилом 72. Например, КПЕР может рассчитывать количество периодов для достижения любой количественной цели (не только удвоение, но и «утроение», увеличение в 5,4 раз и т.п.). Кроме того, КПЕР принимает во внимание регулярные пополнения (в нашем случае они равны нулю).
Пример использования КПЕР вы можете найти в приложении к настоящей статье.

Понравилась статья?
Самое интересное и важное в нашей рассылке
Анонсы свежих статей Информация о вебинарах Советы экспертов
Нажимая на кнопку «Подписаться», я соглашаюсь с политикой конфиденциальности

Правило 72-х: формула удвоения суммы
 Любой инвестор заинтересован в том, чтобы вложенный капитал приумножался. В связи с этим вам будет полезно познакомиться с популярным правилом 72-х, которое описывает удвоение инвестированной суммы. Оно позволяет получить довольно точный ответ на вопрос: когда можно ждать этого удвоения, если вам известны уровни доходности (в обиходе – проценты). Вариантов ответа будет 2, и сама предлагаемая формула хороша, в том числе, тем, что помогает провести оценку доходности вложений на разных интервалах.
Любой инвестор заинтересован в том, чтобы вложенный капитал приумножался. В связи с этим вам будет полезно познакомиться с популярным правилом 72-х, которое описывает удвоение инвестированной суммы. Оно позволяет получить довольно точный ответ на вопрос: когда можно ждать этого удвоения, если вам известны уровни доходности (в обиходе – проценты). Вариантов ответа будет 2, и сама предлагаемая формула хороша, в том числе, тем, что помогает провести оценку доходности вложений на разных интервалах.
«Уберечь деньги труднее, чем добыть их.» Мишель де Монтень
Особенности формулы удвоения суммы и правила 72-х
Есть базовая формула, с помощью которой можно рассчитать, через какое время сумма вложенных средств будет удвоена. Вот как она выглядит:

В ней i – это величина ставки, выраженная в процентном соотношении.
Примечательно, что можно не только установить временной интервал в годах, как это происходит, к примеру, с процентными ставками в банковских учреждениях, но также вычислить свою прибыль за месяц. Логично, что в таком случае и результат удвоения будет получаться также в месяцах. Вы можете применять и этот способ, хотя надо признать, что он довольно неудобный, и в качестве достойной альтернативы используется так называемое правило семидесяти двух .
В чем его объективные преимущества? Вы можете все манипуляции производить прямо в уме, получая готовый результат в течение секунд, и это не преувеличение. Правило очень простое:
Разделите 72 на ставку доходности в % за год, чтобы узнать, через какое время (соответственно, в годах) капитал х2.
Чтобы было более понятно, как делаются все эти вычисления, приведем наглядный пример:
- Что есть? Фиксированная ставка по вкладу в банке – 15%.
- Когда произойдет удвоение: 72:15=4,8 лет.
Соответственно, если ставка увеличится, скажем, до 20%, то (72:20=3,6) удвоение произойдет за 3,6 лет. Если же ставка будет совсем скромной, допустим, 7%, то удвоения придется ожидать 10 лет!
Какие существуют условия? Никаких, кроме одного! Вся прибыль, которую вы будете получать за проценты, вы должны вновь вкладывать с учетом имеющихся условий. Только так расчеты будут точными.
Преимущества правила 72-х
И точная сложная формула с логарифмом, приведенная первой, и правило 72-х работают одинаково верно, но у второго есть ряд объективных преимуществ:
- Оперативность вычислений без необходимости применения калькулятора.
- Число 72, легшее в основу, очень удобно в плане того, что делится практически на любую ставку.
- Практика показывает, что полученный результат довольно точен и приближен к реальности по максимуму.
Уровень точности «под микроскопом»
Да, формула правила 72-х показывает довольно точные данные, но, надо признать, что погрешность в расчетах все-таки существует, если сравнивать с первой довольно устрашающей формулой. Учитывайте это, чтобы быть подготовленным к любым поворотам судьбы. Итак, погрешность будет следующей, если ставки находятся в диапазоне (в %):
- 4-12 – погрешность до 2%
- 12-18 – сбой точности не превышает планку в 4%
- 20 – отклонения не более 5%
Более высокие ставки уже не так позволяют активно применять правило (только разве что для примерных подсчетов):
- 25% — в среднем, до 7%;
- если ставка 30%, то погрешность уже достигает 11%.
Рассмотрим наглядный пример, чтобы проиллюстрировать, каким образом влияет погрешность на результаты:
Допустим, уровень доходности – 12%. Если сделать расчеты по правилу, мы получаем, что сумма станет в 2 раза больше через 6 лет (72:12), но, если посчитать все более точно, то в реальности все произойдет через 6,12 лет. Разница составляет лишь полтора месяца, что, в целом, не изменяет общей картины.
С другой стороны, ставки свыше 20% уже демонстрируют более серьезную погрешность, поэтому в такой ситуации рекомендуем обращаться уже к точной расчетной формуле.
Сфера применения
Где применять это правило? Обычно оно популярно при финансовых вложениях, так как вы можете:
- Узнать, когда можно ждать удвоения.
- Получить результаты по прибыли (примерные) через определенное количество лет.
Например, вы сделали инвестиции в долгосрочные облигации (24 года), и выплата по купону составляет 12% ежегодно. Какой же будет сумма по окончании всего срока? Все просто: так как удвоение происходит раз в 6 лет, то за весь срок соберется 4 периода, и, значит, каждый 6 лет сумма будет увеличиваться в 2 раза. Из этого также следует, что сумма умножается в 4, 8 и 16 раз каждые 12, 18 лет и 24 года.
Конечно, правило 72-х хорошо работает не только на годах. Вы можете применять его и для коротких временных отрезков, например, месяцев. Опять-таки рассмотрим на реальном примере:
Если вы торгуете акциями на фондовом рынке, и средний месячный доход варьируется в пределах 6%, то давайте высчитаем годовую доходность. Капитал удвоится всего за 1 год при условии, что вся прибыль будет вкладываться, начиная работать вместе с уже имеющимся капиталом.
Полезный совет: если вы хотите узнать, когда вложенный капитал увеличится х 3 (то есть, утроится), просто разделите цифру 114 на известный процент.
Правило 72 — это… Что такое Правило 72?
Правило семидесяти (правило 70)[1][2], правило 72[3][4], правило 69[5] — простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент.
Согласно «правилу семидесяти»,
где — годовая ставка инфляции, — срок (в годах) удвоения цен.
Множитель 72 имеет большое количество делителей, соответствующих малым процентам (1, 2, 3, 4, 6, 8, 9, 12) и потому более удобен для использования в качестве делимого по сравнению с более точным значением 69 и более лёгким для запоминания значением 70. По этой причине правило используется как в виде «Правило 70», так и «Правило 72» (но и также «Правило 69»).
История
Первое упоминание о правиле содержится у Луки Пачоли в его математическом труде «Сумма арифметики, геометрии, дробей, пропорций и пропорциональности», вышедшей в свет в 1494 году. Между тем Пачоли не приводит расчёт и не объясняет данное правило, что позволяет сделать вывод о том, что оно было известно и ранее.
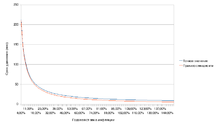 Сравнение точной кривой и её аппроксимации
Сравнение точной кривой и её аппроксимации«Правило семидесяти» является аппроксимацией посредством гиперболы точной формулы
Раскладывая в ряд это выражение при малых , получим . Так как , то наиболее точным при использовании малых процентов среди целых чисел является числитель 69.
Две кривые, задаваемые этими функциями, достаточно хорошо совпадают (см. рисунок).
Погрешность «правила семидесяти»
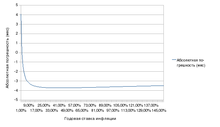 Абсолютная ошибка «правила семидесяти»
Абсолютная ошибка «правила семидесяти»  Относительная ошибка «правила семидесяти»
Относительная ошибка «правила семидесяти»Абсолютная погрешность при использовании «правила семидесяти» не превышает четырёх месяцев, если только годовое значение инфляции .
При точная формула и «правило семидесяти» дают идентичные результаты.
Относительная погрешность начиная с и выше непрерывно растёт, достигая при .
Другие варианты правила
Вместо 70 % также используются числа от 69 % до 72 %. Таким образом, упоминаются «правило 69», «правило 70», «правило 71», «правило 72».
Уточнения
Другие варианты использования
Правило семидесяти может использоваться не только для оценки инфляции, но также для любых других процессов, описываемых экспоненциальной зависимостью.
Срок при этом не обязан исчисляться в годах; нужно только, чтобы коэффициент говорил об изменении величины за ту же единицу времени, в каких измеряется период удвоения .
Кроме того, величина не обязана увеличиваться, она может уменьшатся на за единицу времени. Тогда, конечно, оценивается срок не удвоения величины, а уменьшения её вдвое.
Примеры:
- Оценка срока, в течение которого цены упадут вдвое в результате дефляции, если за год они падают на .
- Оценка срока, в течение которого удвоится вклад в банке при ставке в годовых. (см. Сложные проценты)
- Тактовая частота процессоров растет в среднем на в месяц. Через сколько месяцев эта частота удвоится? (см. закон Мура)
- За тысячелетие количество радиоактивного материала в слитке падает на . Через какое время количество радиоактивного материала сократится вдвое? (см. Закон радиоактивного распада)
Примечания
См. также
 |
Правило 72 — это… Что такое Правило 72?
Правило 72 — Правило семидесяти (правило 70)[1][2], правило 72[3][4], правило 69[5] простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент. Согласно «правилу семидесяти», где … Википедия
Правило 70 — Правило семидесяти (правило 70), правило 72, правило 69 простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент. Согласно «правилу семидесяти», где r годовая ставка… … Википедия
Правило n l — Правило Клечковского (также Правило n+l; за рубежом обычно используется название правило Маделунга) эмпирическое правило, описывающее энергетическое распределение орбиталей в многоэлектронных атомах. Заполнение электронами орбиталей в атоме… … Википедия
ПРАВИЛО — 1. ПРАВИЛО, правила, ср. (спец.). 1. Большая деревянная линейка, применяемая при кладке стен для проверки правильности работы (тех.). 2. Колодка, на которой сапожник расправляет обувь (сапож.). 3. Хвост у борзой собаки (охот.). «Все они, тут же… … Толковый словарь Ушакова
ПРАВИЛО — 1. ПРАВИЛО, правила, ср. (спец.). 1. Большая деревянная линейка, применяемая при кладке стен для проверки правильности работы (тех.). 2. Колодка, на которой сапожник расправляет обувь (сапож.). 3. Хвост у борзой собаки (охот.). «Все они, тут же… … Толковый словарь Ушакова
правило — Закон, узаконение, начало, положение, постановление, норма, принцип, статут. Ср. . См. закон, обыкновенный, обычай .. поставить за правило, принять за правило… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.:… … Словарь синонимов
Правило 6+5 — Правило «6+5» (более известно как лимит «6+5») футбольное правило о разрешённом количестве легионеров в составе команды. Было введено ФИФА в мае 2008 года, но отменено в июне 2010 года по решению Европейской комиссии. Содержание 1 Суть правила 2… … Википедия
ПРАВИЛО — (лат. regula) в объективном смысле равномерность, однообразность бытия, события или действия, сформулированная в понятиях, но еще не познанная как закономерно необходимая. В субъективном смысле – часто предписание (напр., предписание какого либо… … Философская энциклопедия
ПРАВИЛО — ПРАВИЛО, а, ср. 1. Положение, в к ром отражена закономерность, постоянное соотношение каких н. явлений. Грамматические правила. Правила арифметики. 2. Постановление, предписание, устанавливающее порядок чего н. Правила внутреннего распорядка.… … Толковый словарь Ожегова
ПРАВИЛО — ср. закон, постановленье или узаконенье, основанье для действия, в данных случаях, при известных обстоятельствах. Правила для сборщиков, устав. Начальные правила счисленья. Монастырские правила, устав. Правила перед причастьем, наставленья, что… … Толковый словарь Даля
ПРАВИЛО — (1) буравчика определяет направление вектора напряжённости магнитного поля прямолинейного проводника с постоянным током. Если буравчик ввёртывается по направлению тока, то направление его вращения определяет направление магнитных силовых линий… … Большая политехническая энциклопедия
Правило 72 — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Правило сімдесяти (правило 70)[1] — емпіричний спосіб наближеної оцінки терміну, в котрий певне значення зросте вдвічі при постійному зростанні на певний відсоток.
Згідно з «правилом сімдесяти»,
- T≈70r{\displaystyle T\approx {\frac {70}{r}}},
де r — річний відсоток зростання, T — термін (в роках) подвоєння суми. Наприклад, якщо на рахунок в банку вноситься певна сума грошей (наприклад, 1000 гривень) під r = 5 відсотків річних, то сума на рахунку подвоюється (до 2000 гривень) за термін приблизно рівний 14 рокам (T ≈ 70/5).
Множник 72 має більшу кількість дільників, що відповідають малим відсоткам (1, 2, 3, 4, 6, 8, 9, 12), і тому є більш зручним як ділене в порівнянні з більш точним значенням 69 та більш легким для запам’ятовування значенням 70. Тому правило має варіації як «Правило 70», так і як «Правило 72» (але може бути також і в варіації «Правило 69»).
Перша згадка про це правило з’являється в Луки Пачолі в його математичній праці «Сума арифметики, геометрії, дробів, пропорцій та пропорціональності», що вийшла в світ в 1494 році. Між тим, Пачолі не наводить розрахунків і не пояснює дане правило, що дозволяє зробити висновок, що правило це було відомо раніше.
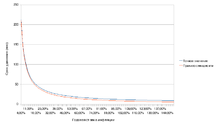 Порівняння точної кривої та її апроксимації
Порівняння точної кривої та її апроксимації«Правило сімдесяти» є апроксимацією через гіперболу точної формули
- T=log1+R2{\displaystyle ~T=\log _{1+R}2}
Розклавши в ряд цей вираз для малих R, отримаєм T≈ln2R{\displaystyle T\approx {\frac {\ln 2}{R}}}. Переходячи від R частин цілого до відсотків (r = R*100), отримаєм T≈100ln2r{\displaystyle T\approx {\frac {100\ln 2}{r}}}. Так як ln 2 ≈ 0,693147, то найбільш точним серед цілих чисел при використанні малих відсотків є ділене 69.
Дві криві, що задаються цими функціями, досить добре збігаються (див. малюнок).
Похибка «правила сімдесяти»[ред. | ред. код]
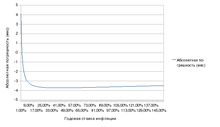 Абсолютна похибка «правила сімдесяти»
Абсолютна похибка «правила сімдесяти»  Відносна похибка «правила сімдесяти»
Відносна похибка «правила сімдесяти»Абсолютна похибка при використанні «правила сімдесяти» не перевищує чотирьох місяців, якщо річний відсоток r > 1,01 %.
При r = 2 % точна формула та «правило сімдесяти» дають майже ідентичні результати.
Відносна похибка починаючи з r = 2 % та вищє постійно зростає, досягаючи 9.86 % при r = 25 %.
Інші варіації правила[ред. | ред. код]
Замість 70 % також використовуються числа від 69 % до 72 %. Таким чином, згадуються «правило 69», «правило 70», «правило 71», «правило 72».
Інші варіанти використання[ред. | ред. код]
Правило сімдесяти може використовуватись не тільки для оцінки зросту грошових сум, але і для будь-яких інших процесів, що описуються експоненційним законом.
Тремін також не має обов’язково розраховуватись в роках; необхідною умовою є лише збіг одиниць вимірювання терміну відсотка зміни r{\displaystyle r} з одиницями вимірювання терміну подвоєння T{\displaystyle T}.
Крім того, значення не обов’язвоко має збільшуватись — воно може також зменшуватись на r відсотків за одиницю терміну. В цьому випадку оцінюється відповідно не термін подвоєння знаяння, а термін його зменшення вдвічі.
Зразки:
- Оцінка терміну, на протязі якого ціни подвояється в результаті інфляції, якщо за рік вони ростуть на r відсотків.
- Тактова частота процесорів росте в средньому на r відсотків в місяць. За скільки місяців вона подвоїться? (див. закон Мура)
- За тисячу років кількість радіоактивного матеріалу в злитку зменшується на r відсотків. За який час кількість радіоактивного матеріалу скоротиться вдвічі? (див. Період напіврозпаду)
Правило 72 — это… Что такое Правило 72?
Правило семидесяти (правило 70)[1][2], правило 72[3][4], правило 69[5] — простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент.
Согласно «правилу семидесяти»,
где — годовая ставка инфляции, — срок (в годах) удвоения цен.
Множитель 72 имеет большое количество делителей, соответствующих малым процентам (1, 2, 3, 4, 6, 8, 9, 12) и потому более удобен для использования в качестве делимого по сравнению с более точным значением 69 и более лёгким для запоминания значением 70. По этой причине правило используется как в виде «Правило 70», так и «Правило 72» (но и также «Правило 69»).
История
Первое упоминание о правиле содержится у Луки Пачоли в его математическом труде «Сумма арифметики, геометрии, дробей, пропорций и пропорциональности», вышедшей в свет в 1494 году. Между тем Пачоли не приводит расчёт и не объясняет данное правило, что позволяет сделать вывод о том, что оно было известно и ранее.
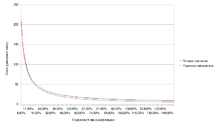 Сравнение точной кривой и её аппроксимации
Сравнение точной кривой и её аппроксимации«Правило семидесяти» является аппроксимацией посредством гиперболы точной формулы
Раскладывая в ряд это выражение при малых , получим . Так как , то наиболее точным при использовании малых процентов среди целых чисел является числитель 69.
Две кривые, задаваемые этими функциями, достаточно хорошо совпадают (см. рисунок).
Погрешность «правила семидесяти»
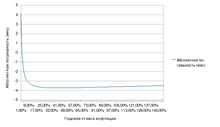 Абсолютная ошибка «правила семидесяти»
Абсолютная ошибка «правила семидесяти»  Относительная ошибка «правила семидесяти»
Относительная ошибка «правила семидесяти»Абсолютная погрешность при использовании «правила семидесяти» не превышает четырёх месяцев, если только годовое значение инфляции .
При точная формула и «правило семидесяти» дают идентичные результаты.
Относительная погрешность начиная с и выше непрерывно растёт, достигая при .
Другие варианты правила
Вместо 70 % также используются числа от 69 % до 72 %. Таким образом, упоминаются «правило 69», «правило 70», «правило 71», «правило 72».
Уточнения
Другие варианты использования
Правило семидесяти может использоваться не только для оценки инфляции, но также для любых других процессов, описываемых экспоненциальной зависимостью.
Срок при этом не обязан исчисляться в годах; нужно только, чтобы коэффициент говорил об изменении величины за ту же единицу времени, в каких измеряется период удвоения .
Кроме того, величина не обязана увеличиваться, она может уменьшатся на за единицу времени. Тогда, конечно, оценивается срок не удвоения величины, а уменьшения её вдвое.
Примеры:
- Оценка срока, в течение которого цены упадут вдвое в результате дефляции, если за год они падают на .
- Оценка срока, в течение которого удвоится вклад в банке при ставке в годовых. (см. Сложные проценты)
- Тактовая частота процессоров растет в среднем на в месяц. Через сколько месяцев эта частота удвоится? (см. закон Мура)
- За тысячелетие количество радиоактивного материала в слитке падает на . Через какое время количество радиоактивного материала сократится вдвое? (см. Закон радиоактивного распада)
Примечания
См. также
 |
Правило 72 — это… Что такое Правило 72?
Правило 72 — Правило семидесяти (правило 70)[1][2], правило 72[3][4], правило 69[5] простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент. Согласно «правилу семидесяти», где … Википедия
Правило 70 — Правило семидесяти (правило 70), правило 72, правило 69 простой способ (приближённой) оценки срока, в течение которого величина вырастет вдвое при постоянном росте на некоторый процент. Согласно «правилу семидесяти», где r годовая ставка… … Википедия
Правило n l — Правило Клечковского (также Правило n+l; за рубежом обычно используется название правило Маделунга) эмпирическое правило, описывающее энергетическое распределение орбиталей в многоэлектронных атомах. Заполнение электронами орбиталей в атоме… … Википедия
ПРАВИЛО — 1. ПРАВИЛО, правила, ср. (спец.). 1. Большая деревянная линейка, применяемая при кладке стен для проверки правильности работы (тех.). 2. Колодка, на которой сапожник расправляет обувь (сапож.). 3. Хвост у борзой собаки (охот.). «Все они, тут же… … Толковый словарь Ушакова
ПРАВИЛО — 1. ПРАВИЛО, правила, ср. (спец.). 1. Большая деревянная линейка, применяемая при кладке стен для проверки правильности работы (тех.). 2. Колодка, на которой сапожник расправляет обувь (сапож.). 3. Хвост у борзой собаки (охот.). «Все они, тут же… … Толковый словарь Ушакова
правило — Закон, узаконение, начало, положение, постановление, норма, принцип, статут. Ср. . См. закон, обыкновенный, обычай .. поставить за правило, принять за правило… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.:… … Словарь синонимов
Правило 6+5 — Правило «6+5» (более известно как лимит «6+5») футбольное правило о разрешённом количестве легионеров в составе команды. Было введено ФИФА в мае 2008 года, но отменено в июне 2010 года по решению Европейской комиссии. Содержание 1 Суть правила 2… … Википедия
ПРАВИЛО — (лат. regula) в объективном смысле равномерность, однообразность бытия, события или действия, сформулированная в понятиях, но еще не познанная как закономерно необходимая. В субъективном смысле – часто предписание (напр., предписание какого либо… … Философская энциклопедия
ПРАВИЛО — ПРАВИЛО, а, ср. 1. Положение, в к ром отражена закономерность, постоянное соотношение каких н. явлений. Грамматические правила. Правила арифметики. 2. Постановление, предписание, устанавливающее порядок чего н. Правила внутреннего распорядка.… … Толковый словарь Ожегова
ПРАВИЛО — ср. закон, постановленье или узаконенье, основанье для действия, в данных случаях, при известных обстоятельствах. Правила для сборщиков, устав. Начальные правила счисленья. Монастырские правила, устав. Правила перед причастьем, наставленья, что… … Толковый словарь Даля
ПРАВИЛО — (1) буравчика определяет направление вектора напряжённости магнитного поля прямолинейного проводника с постоянным током. Если буравчик ввёртывается по направлению тока, то направление его вращения определяет направление магнитных силовых линий… … Большая политехническая энциклопедия
