Самое большое число в мире: как называется
Считается, что концепция чисел впервые возникла, когда доисторические люди начали использовать свои пальцы для подсчета чего-либо. С тех пор человечество прошло долгий путь. Теперь мы используем калькуляторы и компьютеры для подсчета самых больших чисел. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить.
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Как называется самое большое простое число

 Простое число — то, которое делится только на себя и на единицу. В конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число.
Простое число — то, которое делится только на себя и на единицу. В конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число.- Длина его — 24 862 048 символов. Для сравнения: в эпохальном произведении Л.Н. Толстого «Война и мир» около 6-7 миллионов символов, если учитывать знаки препинания и пробелы.
- Это число можно записать следующим образом: 282589933-1
- А читается оно так: два в степени 82589933 минус один.
- Существует целый онлайн-проект GIMPS, нацеленный как раз на поиск самых больших простых чисел. В нем принимают участие математики из разных стран. Поэтому новые рекордсмены появляются часто. Работают ученые, что называется, не за страх, а за деньги. Ведь тому, кто откроет следующее наибольшее простое число Мерсенна достанется 3000 долларов.
Какое самое большое число в мире

 В 1980 году в Книгу рекордов Гиннеса вошло число Грэма (оно же G64 или G), названное в честь американского математика Рональда Грэма. Оно является наибольшим числом, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея.
В 1980 году в Книгу рекордов Гиннеса вошло число Грэма (оно же G64 или G), названное в честь американского математика Рональда Грэма. Оно является наибольшим числом, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея.
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
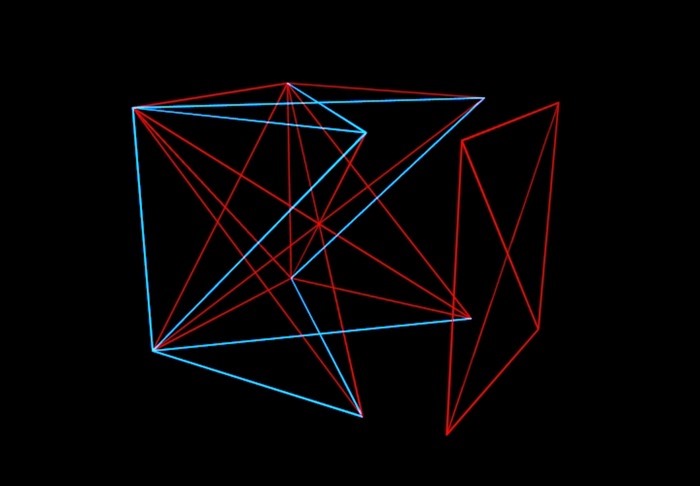

Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
- гугол — 10100;
Или: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - гуголплекс — 10гугол,
то знайте, что этими числами в математике лишь «разминаются», а число Грэма в немыслимое количество раз больше, чем они. И даже больше, чем число Скьюза, находящееся между 1019 и 1,3971672·10316 и приблизительно равное e727,951336108.
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Возможно ли представить и записать число за гранью понимания
Математики не смогут назвать вам точное количество цифр в числе Грэма, не говоря уже о том, чтобы досчитать до него. Известны лишь последние 50 цифр самого большого числа в мире — это …03222348723967018485186439059104575627262464195387.
А вот цифры, с которых начинается G64 неизвестны, и вряд ли когда-либо будут.
Давайте сравним трех монстров: гугол, гуголплекс и число Грэма.
- Гугол — это количество песчинок, которые могут поместиться во вселенной, умноженное на 10 миллиардов. Итак, представьте себе вселенную, заполненную мелкими песчинками — на десятки миллиардов световых лет над Землей, под ней, перед ней, позади нее — бесконечный песок.
Теперь представьте, что в какой-то момент вы берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом. И видите, что на самом деле это не единственное зерно, а 10 миллиардов микроскопических зерен, а все вместе они размером с песчинку. Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
- Для количественной оценки гуголплекса астроном и астрофизик Карл Саган привел пример заполнения всего объема наблюдаемой вселенной мелкими частицами пыли размером приблизительно 1,5 микрометра. Исходя из этого, общее количество различных комбинаций, в которых эти частицы могут быть расположены, будет равно примерно одному гуголплексу.
- А теперь представим, что гуголплекс — это даже не песчинка, а крохотная точка, которую можно рассмотреть лишь в самый мощный микроскоп. И у нас вся вселенная заполнена такими крохотными точками. Так вот, даже это не идет ни в какое сравнение с числом Грэма. Но что, если мы хотим использовать все пространство наблюдаемой вселенной для его записи (предположим, что запись каждой цифры занимает как минимум объём Планка)? Увы, у нас это не выйдет! Но всегда можно пойти другим путем.
Как записать G64 с помощью метода Кнута
В 1976 году американский ученый Дональд Кнут предложил понятие сверхстепеней или нотацию Кнута. Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Вот как выглядит эта нотация: a ↑ b = ab = a × a × a × …, и так b раз.
- Например 3↑3 = 3³.
- Гугол записывается так 10↑10↑2.
- А гуголплекс — 10↑10↑10↑2
Важной особенностью стрелок вверх является то, что они растут очень быстро. Экспонентация растет гораздо быстрее, чем умножение. 2 × 10 — это всего лишь 20, но 2↑10 = 1024. Таким же образом, каждый новый уровень стрелок растет намного быстрее, чем предыдущий уровень.
Если мысленно представить себе степенную башню из троек 3↑↑↑4 то получится конструкция, размером от Земли до Марса. А ведь мы еще даже не дошли до «нижней ступеньки», ведущей нас к числу Грэма.
Мы можем описать число Грэма огромным набором этих стрелок вверх.
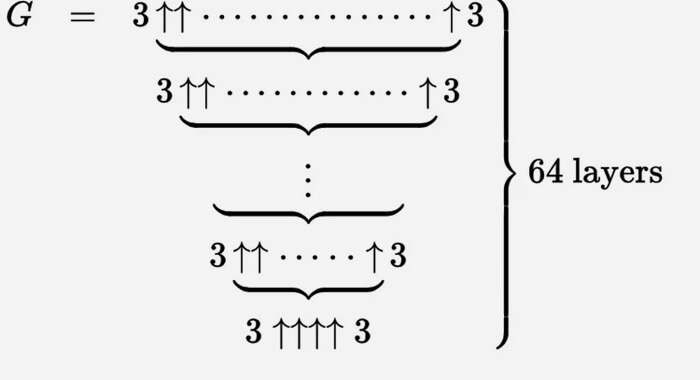

Проще всего думать об этом как об итерационном процессе. Мы начинаем снизу с g 1 = 3 ↑↑↑↑ 3, а затем создаем вторую строку (назовем ее g 2) с g 1 стрелками между тройками.
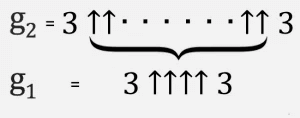

Тогда g 3 — это две тройки, разделенные g 2 стрелками вверх и так далее, пока g 64 с g 63 стрелками между тройками не будет числом Грэма.
Если выбрать продолжительность жизни, равную числу Грэма вместо бессмертия, то результат будет практически одинаков. Даже если предположить, что условия во Вселенной, в Солнечной системе и на Земле вечно останутся неизменными, человеческий мозг никак не мог бы выдержать столь длинный промежуток времени без пагубных изменений.
Как называется самое большое число в мире
Содержание статьи:
ТОП-10 самых больших известных чисел
Как показывает практика, предельного понятия исчисления нет. Когда дети задают вопрос о том, какое самое большое число, ответить можно только в рамках абстрактного понятия.
Чтобы разобраться в этом вопросе и улучшить кругозор, можно изучить ТОП-10 самых больших известных чисел, которые известны человечеству на сегодняшний день.
10^80
Известно как 10 с 80 нулями. В Америке и на территории Англии называют — квинквавигинтиллион. Казалось бы, что может быть больше, ведь это число может охарактеризовать количество частиц во вселенной.
Однако 10 в 80-ой степени далеко не самое большое значение, которое на сегодняшний день известно ученым.
Гугол
Интересный факт, всеми известная поисковая система подарила этому числу большую популярность. Однако значение известно лишь истинным фанатам. Говоря о том, сколько это на самом деле можно выделить число со 100-та нулями.
Термин был придуман в 1938 году, автором стал Милтон Сиротта, которому было всего 9 лет. Существует теория, что когда возраст Земли достигнет гугла, во Вселенной произойдет взрыв черной дыры, что позволит изучить границы за ее пределами.
8,5 х 10^185
С одной стороны это значение обозначает самую маленькую характеристику длины, а с другой это одно из самых больших чисел. В науке обозначается как Длина Планка.
В отличие от других значений имеет распространение в квантовой физике и стала частью теории струн. Говоря о том, сколько же это число значит, можно выделить — 0,00000000000000000000000000000616199 метра.
2^43,112,609 – 1
Интересный факт — в этом числе практически 18 миллионов цифр. Обнаружили сравнительно недавно, т.е в 2008 году в ходе GIMPS.
Несмотря на свою величину, занимает лишь 47 место в порядке размера.Гуголплекс
Впервые те, кто не сталкивался плотно с наукой, могли услышать это значение в фильме «Назад Будущее». Во время одного из мозговых штурмов Эммет Браун обронил слово Гуголплекс.
Как показали успешные поиски фанатов — такое значение существует. Гуголплекс — равен 10-ти в степени гугол. Для абстрактного понятия можно представить, что эта сумма больше чем частиц во Вселенной, которые были изучены за все существование науки.
Числа Скьюза
Достаточно много теорий по поводу величины этого значений. Однако если взять за основу самую популярную, то окажется, что Скьюз больше чем гуголплекс в несколько раз. Джон Литтлвуд в далеком 1914 году делал первые открытия, которые доказывали существование этого числа.
Однако доказать значение получилось только у Стенли Скьюза в 1933, после того, как он взял в основу теорию Римана.
Теория Пуанкаре
Число и одновременно теория о том, сколько бы времени понадобилось бы нашей Вселенной, что вернуться в исходное состояние.
Говоря простым языком, 10^10^10^10^10^1,1 лет нужно для того, чтобы история человечества вновь повторилась.
Значение Грэма
Одно из самых больших чисел, которое стало известно лишь в конце 80-х. Для его простой записи используют метод Кнута. Запомнить написание практически невозможно. Чтобы оценить масштабность значения, можно представить как число Пуанкаре умножают на несколько раз.
Особенность Грэма заключается в том, что для записи использую несколько уровней, самая простая выглядит так: G=f64(4), где f(n)=3↑^n3.
Если разбирать слои, то можно понять 3↑↑↑↑3 это уже больше чем число Пуанкаре. Одни из интересных фактов — первые числа пока неизвестно миру, а вот последние (всего 10) Грэм все же успел вычислить — 2464195387.
Бесконечность
С научной точки зрения число имеет огромную величину. Она настолько большая, что порой человеческой возможности абстракции не хватает фантазии чтобы ее представить.
Интересный факт, бесконечность ровно на половину делится на четные и нечетные числа. Ученые сами до конца не выяснили до конца какую величину обозначает мера «бесконечность». Ведь сегодня известно лишь 10^80 частиц.
Также значение бесконечности доказывает, что если вся вселенная устроена по принципу земли — т.е атомы складываются рано или поздно воедино, это значит копия планеты в теории может существовать. Более того, дублироваться может и сама вселенная.
Однако в такую теорию верят далеко не все ученые, например Дорон Зильбергер из Израиля настаивает на то, что вскоре найдется число больше бесконечности.
Когда это произойдет не уточняется, ведь предельное число бесконечности лишь абстрактное понимание. Тем не менее на сегодняшний день именно о бесконечности говорят в школах, и именно это значение является верховным в математической философии.
∞ + 1
Несмотря на абстрактность теории о бесконечности, есть идея, что это не конечное число. Как показывает практика, у каждого числа есть своя принадлежность, т.е к плюсу или минусу.
Если из суммы натуральных чисел вычесть сумму их квадрата — можно получить — ∞. Это значит, что границы бесконечности не могут заканчиваться только на одной теории о конечном числе. Чтобы углубиться в этот вопрос можно изучить метод Лопиталя.
Системы наименования чисел — Википедия
В европейской традиции исторически сложились два варианта построения системы наименования чисел.
Термин «миллион» итальянского происхождения и встречается уже в первой печатной арифметике (анонимной), вышедшей в итальянском городе Тревизо в 1478 году, и ещё ранее в нематематической книге путешественника Марко Поло (умер в 1324 году), а в форме «миллио» — уже в рукописи 1250 года.
В рукописи французского математика XV века Никола Шюке впервые появляются термины «биллион» — 1012, «триллион» — 1018 и дальнейшие; в печатном руководстве биллион в значении 1012 появляется в 1602 году.
В XVII веке во Франции начали употреблять короткую шкалу: «биллион» — 109, «триллион» — 1012 и т. д.
Слово «миллиард», имевшее вначале значение 1012, получило значение 109 (тысячи миллионов) в «Арифметике» Траншана (1558) и употреблялось во Франции в XIX веке наравне со словом «биллион». В Германии это слово вошло в употребление лишь после получения от Франции 5 миллиардов контрибуции после франко-прусской войны 1871 года.
Для чтения многозначных чисел анонимная рукопись 1200 года впервые рекомендует разбить цифры на группы по 3 или отмечать группы точками вверху или дугами; это же затем рекомендует Леонардо Пизанский (1228). К этой системе приходят и последующие авторы.
 Использование систем наименования чисел в мире:
Использование систем наименования чисел в мире:| короткая шкала длинная шкала | обе шкалы другие системы |
В России первоначально была введена система наименования чисел с длинной шкалой, и, по-видимому, в печатном виде впервые в 1703 году в «Арифметике» Л. Ф. Магницкого. Однако в конце XVIII века, в царствование императора Павла I, вслед за Францией произошёл переход на короткую шкалу. Так, в опубликованном в 1798 году переводе части первой — «Арифметика» — «Курса математики» Этьенна Безу введена система наименования чисел с короткой шкалой, при том, что ещё в опубликованной в 1791 году книге «Арифметика или числовник» Н. Г. Курганова (1725 или 1726—1796) используется длинная шкала.
В 1948 году IX Генеральная конференция по мерам и весам приняла предложение Международного комитета мер и весов, рекомендующего для европейских стран применение длинной шкалы. Франция вернулась к системе с длинной шкалой, а в России продолжалось использование системы с короткой шкалой, которая была заимствована во Франции ранее. Однако, использование длинной шкалы предусматривается рекомендацией Совета экономической взаимопомощи PC 2625—70 «Основные математические обозначения» [1], где приводятся основные математические обозначения, употребляемые в нормативно-технической документации, научной и технической литературе и в школьных учебниках. Последнее позволяет утверждать, что официально во всех странах, образовавшихся после распада СССР, с 1948 года действует именно длинная система наименований чисел, хотя фактически продолжает применяться короткая система.
В случае короткой шкалы все названия больших чисел строятся так: в начале идёт латинское числительное[2], обозначающее степень тысячи, а в конце к нему добавляется суффикс «-иллион». Исключение составляет название «миллион», которое образовано от латинского числительного mille «тысяча» при помощи увеличительного суффикса «-он» -one). Так получаются числа — миллион, биллион[3], триллион, квадриллион, квинтиллион, секстиллион и т. д. Система наименования чисел с короткой шкалой используется в России[источник не указан 25 дней
Названия чисел в этой системе строятся так: к латинскому числительному[2], обозначающему степень миллиона, добавляют суффикс «-он», название следующего числа (в 1000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-ард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по этой системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард».
В настоящее время применяется в большинстве франкоязычных, скандинавских, испаноязычных [4] и португалоязычных стран, кроме Бразилии.
Таблица от значения к названию[править | править код]
| Порядок | Значение | число нулей | Короткая шкала | Длинная шкала | СИ | ||
|---|---|---|---|---|---|---|---|
| Название | Логика построения | Название | Логика построения | ||||
| 0 | 100 | 0 | один | 10001 + (-1) | один | 1 000 0000 | |
| 1 | 103 | 3 | тысяча | 10001 + 0 | тысяча | 1 000 0000,5 | кило- |
| 2 | 106 | 6 | миллион | 10001 + 1 | миллион | 1 000 0001,0 | мега- |
| 3 | 109 | 9 | биллион (миллиард)[3] | 10001 + 2 | 1 000 0001,5 | гига- | |
| 4 | 1012 | 12 | триллион | 10001 + 3 | биллион | 1 000 0002,0 | тера- |
| 5 | 1015 | 15 | квадриллион | 10001 + 4 | биллиард (тысяча биллионов) | 1 000 0002,5 | пета- |
| 6 | 1018 | 18 | квинтиллион | 10001 + 5 | триллион | 1 000 0003,0 | экса- |
| 7 | 1021 | 21 | секстиллион | 10001 + 6 | триллиард (тысяча триллионов) | 1 000 0003,5 | зетта- |
| 8 | 1024 | 24 | септиллион | 10001 + 7 | квадриллион | 1 000 0004,0 | иотта- |
| 9 | 1027 | 27 | октиллион | 10001 + 8 | квадриллиард (тысяча квадриллионов) | 1 000 0004,5 | |
| 10 | 1030 | 30 | нониллион | 10001 + 9 | квинтиллион | 1 000 0005,0 | |
| 11 | 1033 | 33 | дециллион | 10001 + 10 | квинтиллиард (тысяча квинтиллионов) | 1 000 0005,5 | |
| 12 | 1036 | 36 | ундециллион | 10001 + 11 | секстиллион | 1 000 0006,0 | |
| 13 | 1039 | 39 | дуодециллион | 10001 + 12 | секстиллиард (тысяча секстиллионов) | 1 000 0006,5 | |
| 14 | 1042 | 42 | 10001 + 13 | септиллион | 1 000 0007,0 | ||
| 15 | 1045 | 45 | кваттуордециллион | 10001 + 14 | септиллиард (тысяча септиллионов) | 1 000 0007,5 | |
| 16 | 1048 | 48 | квиндециллион | 10001 + 15 | октиллион | 1 000 0008,0 | |
| 17 | 1051 | 51 | сексдециллион | 10001 + 16 | октиллиард (тысяча октиллионов) | 1 000 0008,5 | |
| 18 | 1054 | 54 | септендециллион | 10001 + 17 | нониллион | 1 000 0009,0 | |
| 19 | 1057 | 57 | октодециллион | 10001 + 18 | нониллиард (тысяча нониллионов) | 1 000 0009,5 | |
| 20 | 1060 | 60 | новемдециллион | 10001 + 19 | дециллион | 1 000 00010,0 | |
| 21 | 1063 | 63 | вигинтиллион | 10001 + 20 | дециллиард (тысяча дециллионов) | 1 000 00010,5 | |
| 22 | 1066 | 66 | унвигинтиллион | 10001 + 21 | |||
| 23 | 1069 | 69 | дуовигинтиллион | 10001 + 22 | |||
| 24 | 1072 | 72 | тревигинтиллион | 10001 + 23 | |||
| 25 | 1075 | 75 | кваттуорвигинтиллион | 10001 + 24 | |||
| 26 | 1078 | 78 | квинвигинтиллион | 10001 + 25 | |||
| 27 | 1081 | 81 | сексвигинтиллион | 10001 + 26 | |||
| 28 | 1084 | 84 | септенвигинтиллион | 10001 + 27 | |||
| 29 | 1087 | 87 | октовигинтиллион | 10001 + 28 | |||
| 30 | 1090 | 90 | новемвигинтиллион | 10001 + 29 | |||
| 31 | 1093 | 93 | тригинтиллион | 10001 + 30 | |||
| 32 | 1096 | 96 | унтригинтиллион | 10001 + 31 | |||
| 33 | 1099 | 99 | дуотригинтиллион | 10001 + 32 | |||
| 34 | 10102 | 102 | третригинтиллион | 10001 + 33 | |||
| 35 | 10105 | 105 | кваттуортригинтиллион | 10001 + 34 | |||
| 36 | 10108 | 108 | квинтригинтиллион | 10001 + 35 | |||
| 37 | 10111 | 111 | секстригинтиллион | 10001 + 36 | |||
| 38 | 10114 | 114 | септентригинтиллион | 10001 + 37 | |||
| 39 | 10117 | 117 | октотригинтиллион | 10001+38 | |||
Таблица от названия к значению[править | править код]
- Виленкин Н. Я. От нуля до декаллиона // Квант, 1989, № 3. С. 20.
- Депман И. Я. История арифметики // 2-е изд., испр. М.: Просвещение, 1965. 416 с.
- Мендаль З. О названиях и начертании больших чисел. // Техника молодежи 1938 г., № 1, стр. 58.
- Перельман Я. И. Занимательная арифметика // 1926 год. Ленинград, «Время», 192 c.
- Киселев А. П. Систематический курс арифметики // 1912 год.
- Безу Э. Курс математики. Арифметика // М., 1806. 191 с. 2-е изд.
- Курганов Н. Г. Арифметика или числовник. Часть 1 // СПб., 1791
- Магницкий Л. Ф. Арифметика // 1703 год
- Керн С. A Zillion Troubles
- Козловский С. Самое большое число в мире
Самое большое число в мире

“Я вижу скопления смутных чисел, которые скрывается там, в темноте, за небольшим пятном света, которое дает свеча разума. Они шепчутся друг с другом; сговариваясь кто знает о чем. Возможно, они нас не очень любят за захват их меньших братишек нашими умами. Или, возможно, они просто ведут однозначный числовой образ жизни, там, за пределами нашего понимания’’.
Дуглас Рэй
Продолжаем нашу рубрику САМОГО САМОГО. Сегодня у нас числа …
Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности.
А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название?
Сейчас мы все узнаем …
Существуют две системы наименования чисел — американская и английская.
Американская система постороена довольно просто. Все названия больших чисел строятся так: в начале идет латинское порядковое числительное, а в конце к ней добавляется суффикс -иллион. Исключение составляет название «миллион» которое является названием числа тысяча (лат. mille) и увеличительного суффикса -иллион (см. таблицу). Так получаются числа — триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион. Американская система используется в США, Канаде, Франции и России. Узнать количество нулей в числе, записанном по американской системе, можно по простой формуле 3·x+3 (где x — латинское числительное).
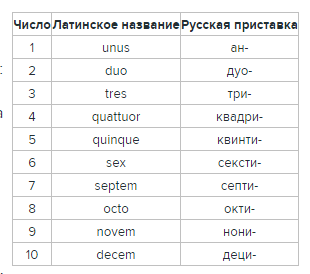
Английская система наименования наиболее распространена в мире. Ей пользуются, например,
Самая большая цифра в мире • Интернет
Самая большая цифра в мире
10 в 3003 степени

Споры о том, какая самая большая цифра в мире, ведутся постоянно. Разные системы исчисление предлагают разные варианты и люди не знают чему верить, и какую именно цифру считать самой большой.
Данный вопрос интересовал ученых еще со времен Римской империи. Наибольшая загвоздка кроется в определении, что такое «число», и что такое «цифра». В свое время люди длительное время считали самым большим числом дециллион, то есть 10 в 33 степени. Но, после того, как ученые стали активно изучать американскую и английскую метрические системы, было обнаружено, что самое большое число в мире это 10 в 3003 степени – миллеиллион. Люди в повседневной жизни считают, что самой большой цифрой является триллион. Причем, это довольно формально, поскольку после триллиона, названия просто не даются, ведь счет начинается слишком сложный. Однако, чисто теоретически, количество нулей можно прибавлять до бесконечности. Поэтому представить даже чисто визуально триллион и то, что следует за ним, является практически невозможным.
В римских цифрах

С другой стороны, определение «цифры» в понимании математиков, это немного иное. Под цифрой подразумевается знак, который принят повсеместно и используется для того, чтобы обозначить количество, выраженное в числовом эквиваленте. Под вторым понятием «число» подразумевается выражение количественных характеристик в удобном виде через использование цифр. Из этого следует, что числа состоят из цифр. Также важно то, что цифра обладает знаковыми свойствами. Они обусловлены, узнаваемы, неизменяемы. Числа тоже имеют знаковые свойства, но они вытекают из того, что числа состоят из цифр. Отсюда можно сделать вывод, что триллион, это вовсе не цифра, а число. Тогда, какая же самая большая цифра в мире, если это не триллион, который является числом?
Важно то, что цифры используются, как составляющие числа, но и не только это. Цифра впрочем это то же число, если мы говорим о каких-то вещах, считая их от нуля и до девяти. Такая система признаков применяется не только к привычным нам арабским цифрам, но также и к римским I, V, X, L, C, D, M. Это римские цифры. С другой стороны V I I I – это римское число. В арабском исчислении ему соответствует цифра восемь.
В арабских цифрах

Таким образом, получается, что цифрами считаются единицы счета от нуля до девяти, а все остальное числа. Отсюда вывод, что самой большой цифрой в мире получается девять. 9 – знак, а число это простая количественная абстракция. Триллион это число, и никак не цифра, а потому не может быть самой большой цифрой в мире. Триллионом можно назвать самое большое число в мире и то чисто номинально, поскольку числа можно считать до бесконечности. Число цифр же строго ограничено – от 0 и до 9.
Также следует помнить, что цифры и числа разных систем исчисления не совпадают, как мы видели из примеры с арабскими и римскими числами и цифрами. Это происходит потому, что цифры и числа это простые понятия, которые выдумывает сам человек. Поэтому число одной системы исчисления с легкостью может быть цифрой другой и наоборот.

Таким образом, самое большое число является неисчислимым, ведь его можно продолжать складывать до бесконечности из цифр. Что касается, собственно цифр, то в общепринятой системе, самой большой цифрой считается 9.
Большие числа — Википедия
Материал из Википедии — свободной энциклопедии
Неформально (обычно в развлекательной математике и научно-популярной литературе) большими числами называют числа, значительно превосходящие числа, используемые в повседневной жизни.
Изучение больших чисел и их номенклатуры иногда называются термином гугология (англ. googology)[1][2][3]. Термин был образован как комбинация слов «гугол» (классическое большое число) и «логос» (учение). Термин введён любителем математики Джонатаном Бауэрсом[2].
Несмотря на то что гугология — современный термин, история изучения человеком больших чисел уходит в глубокую древность.
III век до н. э. — Архимед в своём труде Псаммит представил нотацию, позволяющую записывать числа до 108×1016{\displaystyle 10^{8\times 10^{16}}}[4]. В связи с этим его иногда называют первым «гугологистом»[2].
I век н. э. — В буддистском священном тексте Аватамсака-сутра было упомянуто число ≈101032{\displaystyle \approx 10^{10^{32}}}
1928 год — Вильгельм Аккерман опубликовал свою функцию.
1940 год — Эдвард Казнер описал числа гугол (10100{\displaystyle 10^{100}}) и гуголплекс (1010100{\displaystyle 10^{10^{100}}})[5].
1947 год — Р. Гудштейн[en] дал наименование операциям тетрации (a↑↑b{\displaystyle a\uparrow \uparrow b}), пентации (a↑↑↑b{\displaystyle a\uparrow \uparrow \uparrow b}) и гексации (a↑4b{\displaystyle a\uparrow ^{4}b})[6].
1970 год — С. Вайнер дал определение быстрорастущей иерархии[7].
1976 год — Дональд Кнут изобрёл стрелочную нотацию[8] (предел ω{\displaystyle \omega } в терминологии быстрорастущей иерархии).
1977 год — Мартин Гарднер в журнале Scientific American описал число Грэма[9] (G=g(64)=f64(4){\displaystyle G=g(64)=f^{64}(4)}, где f(n)=3↑n3{\displaystyle f(n)=3\uparrow ^{n}3}. Функция g(n){\displaystyle g(n)} имеет скорость роста порядка ω+1{\displaystyle \omega +1}).
1983 год — была изобретена нотация Штейнгауза — Мозера[10](предел ω{\displaystyle \omega }).
1995 год — Джон Конвей изобрёл цепную стрелочную нотацию[11](предел ω2{\displaystyle \omega ^{2}}).
2002 год — Д. Бауэрс (J. Bowers) опубликовал свои нотацию массива[12][13] (предел ωω{\displaystyle \omega ^{\omega }}) и расширенную нотацию массива (предел ωωω{\displaystyle \omega ^{\omega ^{\omega }}}).
2002 год — Х. Фридман[en] дал определение функции TREE(n), имеющей скорость роста θ(Ωωω){\displaystyle \theta (\Omega ^{\omega }\omega )}.
2006 год — Х. Фридман дал определение быстрорастущим функциям SCG(n) и SSCG(n).
2007 год — Бауэрс определил ещё более мощную нотацию BEAF (данная нотация хорошо определена до ε0{\displaystyle \varepsilon _{0}}, числа, превосходящие этот уровень, вызывают противоречивость оценок).
Математические объекты, имеющие отношения к гугологии (в том числе большие числа), называются гугологизмами. В настоящее время наименования даны для нескольких тысяч чисел, превосходящих гугол. Ниже приведён список некоторых гугологизмов и их выражения в наиболее известных нотациях[14]. Перед выражением в той нотации, в которой число было записано автором, стоит знак равенства, выражения для того же числа в других нотациях представляют собой аппроксимации.
| имя числа | степень десяти | нотация Кнута | нотация Конвея | Нотация Бауэрса (нотация массива) | Нотация Сайбиана (гипер-E нотация) | быстрорастущая иерархия |
|---|---|---|---|---|---|---|
| Гугол | =10100{\displaystyle =10^{100}} | 10↑100{\displaystyle 10\uparrow 100} | 10→100{\displaystyle 10\rightarrow 100} | {10,100}{\displaystyle \{10,100\}} | E100{\displaystyle E100} | f2(324){\displaystyle f_{2}(324)} |
| Гуголплекс | =1010100{\displaystyle =10^{10^{100}}} | 10↑10↑100{\displaystyle 10\uparrow 10\uparrow 100} | 10→(10→100){\displaystyle 10\rightarrow (10\rightarrow 100)} | {10,{10,100}}{\displaystyle \{10,\{10,100\}\}} | E100#2{\displaystyle E100\#2} | f22(324){\displaystyle f_{2}^{2}(324)} |
| Гиггол (Giggol) | 101010⋯1010⏟100 десяток{\displaystyle \underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} _{\text{100 десяток}}} | 10↑2100{\displaystyle 10\uparrow ^{2}100} | 10→100→2{\displaystyle 10\rightarrow 100\rightarrow 2} | ={10,100,2}{\displaystyle =\{10,100,2\}} | E1#100{\displaystyle E1\#100} | f3(100){\displaystyle f_{3}(100)} |
| Гаггол (Gaggol) | 101010⋯1010⏟101010⋯1010⏟⋮⏟101010⋯1010⏟10 десяток}100 {\displaystyle \left.{\begin{matrix}&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&\underbrace {\quad \quad \;\;\vdots \quad \quad \;\;} \\&&\underbrace {10^{10^{10^{\cdots ^{10^{10}}}}}} \\&&{\text{10 десяток}}\end{matrix}}\right\}{\text{100 }}} | 10↑3100{\displaystyle 10\uparrow ^{3}100} | 10→100→3{\displaystyle 10\rightarrow 100\rightarrow 3} | ={10,100,3}{\displaystyle =\{10,100,3\}} | E1#1#100{\displaystyle E1\#1\#100} | f4(100){\displaystyle f_{4}(100)} |
| Бугол (Boogol) | 10↑10010{\displaystyle 10\uparrow ^{100}10} | 10→10→100{\displaystyle 10\rightarrow 10\rightarrow 100} | ={10,10,100}{\displaystyle =\{10,10,100\}} | E100##100{\displaystyle E100\#\#100} | f101(100){\displaystyle f_{101}(100)} | |
| Число Грэма | =3↑↑⋯↑↑3⏟3↑↑⋯↑↑3⏟⋮⏟3↑↑⋯↑↑3⏟3↑43стрелок}64 {\displaystyle =\left.{\begin{matrix}&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&\underbrace {\quad \quad \;\;\vdots \quad \quad \;\;} \\&&\underbrace {3\uparrow \uparrow \cdots \uparrow \uparrow 3} \\&&3\uparrow ^{4}3{\text{стрелок}}\end{matrix}}\right\}{\text{64 }}} | 3→3→64→2{\displaystyle 3\rightarrow 3\rightarrow 64\rightarrow 2} | {3,65,1,2}{\displaystyle \{3,65,1,2\}} | E(3)3##4#64{\displaystyle E(3)3\#\#4\#64} | fω+1(64){\displaystyle f_{\omega +1}(64)} | |
| Траддом (Traddom)[15] | 10→10→11→4{\displaystyle 10\rightarrow 10\rightarrow 11\rightarrow 4} | {10,10,3,2}{\displaystyle \{10,10,3,2\}} | E10##10##4{\displaystyle E10\#\#10\#\#4} | =fω+3(10){\displaystyle =f_{\omega +3}(10)} | ||
| Биггол (Biggol) | 10→10→10→100{\displaystyle 10\rightarrow 10\rightarrow 10\rightarrow 100} | ={10,10,100,2}{\displaystyle =\{10,10,100,2\}} | E100##100##100{\displaystyle E100\#\#100\#\#100} | fω.2(100){\displaystyle f_{\omega .2}(100)} | ||
| Трултом (Trultom) | 10→10→10→10→11{\displaystyle 10\rightarrow 10\rightarrow 10\rightarrow 10\rightarrow 11} | {10,10,10,3}{\displaystyle \{10,10,10,3\}} | E10###4{\displaystyle E10\#\#\#4} | =fω.3(10){\displaystyle =f_{\omega .3}(10)} | ||
| Тругол (Troogol) | 10→10→⋯→10⏟101→{\displaystyle \underbrace {10\rightarrow 10\rightarrow \cdots \rightarrow 10} _{101\quad \rightarrow }} | ={10,10,10,100}{\displaystyle =\{10,10,10,100\}} | E100###100{\displaystyle E100\#\#\#100} | fω2(100){\displaystyle f_{\omega ^{2}}(100)} |
Числа, приведённые ниже, находятся уже за пределами применения нотаций Кнута и Конвея.
| имя числа | нотация Бауэрса (BEAF) | нотация Сайбиана | быстрорастущая иерархия |
|---|---|---|---|
| Квадругол (Quadroogol) | ={10,10,10,10,100}{\displaystyle =\{10,10,10,10,100\}} | E100####100{\displaystyle E100\#\#\#\#100} | fω3(100){\displaystyle f_{\omega ^{3}}(100)} |
| Квадрексом (Quadrexom) | {10,10,10,10,10,10}{\displaystyle \{10,10,10,10,10,10\}} | E10#####10{\displaystyle E10\#\#\#\#\#10} | =fω4(10){\displaystyle =f_{\omega ^{4}}(10)} |
| Квинтугол (Quintoogol) | ={10,10,10,10,10,100}{\displaystyle =\{10,10,10,10,10,100\}} | E100#####100{\displaystyle E100\#\#\#\#\#100} | fω4(100){\displaystyle f_{\omega ^{4}}(100)} |
| Губол (Goobol) | ={10,100(1)2}={\displaystyle =\{10,100(1)2\}=} ={10,10,10,⋯,10,10}⏟100десяток{\displaystyle =\underbrace {\{10,10,10,\cdots ,10,10\}} _{100\quad {\text{десяток}}}} | E100#99100{\displaystyle E100\#^{99}100} | fω98(100){\displaystyle f_{\omega ^{98}}(100)} |
| Бубол (Boobol) | ={10,10,100(1)2}{\displaystyle =\{10,10,100(1)2\}} | E100#^#100##100 | fωω+99(100){\displaystyle f_{\omega ^{\omega }+99}(100)} |
| Трубол (Troobol) | ={10,10,10,100(1)2}{\displaystyle =\{10,10,10,100(1)2\}} | E100#^#100###101 | fωω+ω2(100){\displaystyle f_{\omega ^{\omega }+\omega ^{2}}(100)} |
| Квадрубол (Quadroobol) | ={10,10,10,10,100(1)2}{\displaystyle =\{10,10,10,10,100(1)2\}} | E100#^#100####101 | fωω+ω3(100){\displaystyle f_{\omega ^{\omega }+\omega ^{3}}(100)} |
| Гутрол (Gootrol) | ={10,100(1)3}{\displaystyle =\{10,100(1)3\}} | E100#^#100#^#100 | fωω.2(100){\displaystyle f_{\omega ^{\omega }.2}(100)} |
| Госсол (Gossol) | ={10,10(1)100}{\displaystyle =\{10,10(1)100\}} | E100#^#*#100 | fωω+1(100){\displaystyle f_{\omega ^{\omega +1}}(100)} |
| Моссол (Mossol) | ={10,10(1)10,100}{\displaystyle =\{10,10(1)10,100\}} | E100#^#*##100 | fωω+2(100){\displaystyle f_{\omega ^{\omega +2}}(100)} |
| Боссол (Bossol) | ={10,10(1)10,10,100}{\displaystyle =\{10,10(1)10,10,100\}} | E100#^#*###100 | fωω+3(100){\displaystyle f_{\omega ^{\omega +3}}(100)} |
| Троссол (Trossol) | ={10,10(1)10,10,10,100}{\displaystyle =\{10,10(1)10,10,10,100\}} | E100#^#*####100 | fωω+4(100){\displaystyle f_{\omega ^{\omega +4}}(100)} |
| Дубол (Dubol) | ={10,100(1)(1)2}{\displaystyle =\{10,100(1)(1)2\}} | E100#^#*#^#100 | fωω.2(100){\displaystyle f_{\omega ^{\omega .2}}(100)} |
| Дутрол (Dutrol) | ={10,100(1)(1)3}{\displaystyle =\{10,100(1)(1)3\}} | E100#^#*#^#100#^#*#^#100 | fωω.2.2(100){\displaystyle f_{\omega ^{\omega .2}.2}(100)} |
| Колоссол (Colossol) | ={10,10(3)2}{\displaystyle =\{10,10(3)2\}} | E10#^###10 | fωω3(10){\displaystyle f_{\omega ^{\omega ^{3}}}(10)} |
| Тероссол (Terossol) | ={10,10(4)2}{\displaystyle =\{10,10(4)2\}} | E10#^####10 |
Как называется самое большое число в мире?
Людей окружают числа постоянно. Номера домов и деньги, почтовые индексы и номера телефонов… да и многое другое тоже. Все могут сами, думается, продолжить этот список.
Но – какое же из чисел самое большое? Казалось бы, ответа на этот вопрос быть не может. Числа не имеют никакого ограничения. Всегда можно к любому числу прибавить ещё какое-то – и исходное сразу станет больше.
Попробуем всё-таки разобраться. Обратимся к тому, какие есть наименования гигантских цифр. И сразу примем во внимание, что в мире существуют сразу две системы названия чисел.
В англо-американской схеме к латинскому числительному прибавляется суффикс «иллион». Исключение составляет, само собой, обычный «миллион», но это и неудивительно – данное число появилось в конце средневековья, и тогда казалось Воистину Большим.
Триллион – это число с двенадцатью нулями, квинтиллион с восемнадцатью, иониллион с тридцатью. Здесь названы, понятное дело, не все такие числительные… но в любом случае разница между соседними из них – порядок. Английская версия немного отличается. Триллион в ней имеет 21 ноль, триллиард – 24 ноля. Таким образом, окончания иллион и иллиард чередуются между собой.
В нашей стране используется американская схема, с той разницей, что миллиард отсчитывается «по-английски». Кстати, по американской системе наибольшим числом будет миллеиллион – цифра с тремя тысячами тремя нулями.
И – всё? А вот и нет! Ведь есть ещё внесистемные числительные. «Мириада», например – это сотня сотен, или число с десятью тысячами нулей. Гугол – единица со ста нулями за собой. Гуголплекс – это цифра с гуголом (!) нолей. G, или число Грэма – самое большое из применяющихся в математических исследованиях. Сформулировано оно было достаточно поздно, лишь в семидесятые годы прошлого века (тогда математика впервые достигла нужного рубежа). Записывают число Грэма при помощи особого приёма – так называемой сверхстепени, отображаемой для большего удобства вертикальными стрелками.
До известного уровня использование степени облегчает запись сверхбольших цифр. Но в самой «верхней» их области это уже сложно. Поэтому самые-самые крупные цифры записывают не арифметически, а геометрически.
Американская схема построения числительных используется в Канаде и Франции, английская – в Испании. Пресловутая «мириада» крайне редко используется в математике. Гораздо чаще она употребляется в обычной речи, как указание просто на «колоссальное множество чего-то».
https://interesnie-fakti.net/
