Значки в математике – Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info

Сумма (математика) — Википедия

У этого термина существуют и другие значения, см. сумма.

Су́мма (лат. summa — итог, общее количество) в математике — это результат операции сложения числовых величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:

a+b=b+a{\displaystyle a+b=b+a}

a+(b+c)=(a+b)+c{\displaystyle a+(b+c)=(a+b)+c}

(a+b)⋅c=a⋅c+b⋅c{\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}

c⋅(a+b)=c⋅a+c⋅b{\displaystyle c\cdot (a+b)=c\cdot a+c\cdot b}

В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы слагаемых множеств, взятые без повторений.

Операция сложение (нахождение суммы) может быть определена для более сложных алгебраических структур. Сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры. В теории категорий определяется понятие суммы объектов.

Пусть в множестве N{\displaystyle \mathbb {N} } находится a{\displaystyle a} элементов, образующих подмножество A{\displaystyle A}, и b{\displaystyle b} элементов, образующих подмножество B{\displaystyle B} (A⊂N,B⊂N{\displaystyle A\subset \mathbb {N} ,B\subset \mathbb {N} }, a и b — натуральные числа). Тогда арифметической суммой a+b{\displaystyle a+b} будет количество элементов c{\displaystyle c}, образующих подмножество C⊂N{\displaystyle C\subset \mathbb {N} }, полученное при дизъюнктном объединении двух исходных подмножеств C=A⊔B;{\displaystyle C=A\sqcup B;}.

Сумму математически обозначают заглавной греческой буквой Σ (сигма).

∑i=⁡mnai=am+am+1+am+2+⋯+an−1+an{\displaystyle \sum _{i\mathop {=} m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}}

где: i — индекс суммирования; a_i — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.^[1]

В программировании данной процедуре соответствует цикл for.

Примеры записи

∑i=⁡1100i=1+2+3+4+…+99+100{\displaystyle \sum _{i\mathop {=} 1}^{100}i=1+2+3+4+…+99+100}

∑i=⁡36i2=32+42+52+62=86{\displaystyle \sum _{i\mathop {=} 3}^{6}i^{2}=3^{2}+4^{2}+5^{2}+6^{2}=86}

Указание границ может опускаться из записи, если они ясны из контекста:

∑ai2=∑i=⁡1nai2{\displaystyle \sum a_{i}^{2}=\sum _{i\mathop {=} 1}^{n}a_{i}^{2}}

Итератор может быть выражением, тогда переменная оформляется со скобками как функция «f(){\displaystyle f()}». Например, сумма всех натуральных чисел k{\displaystyle k} в определённом диапазоне:

∑0≤k<100f(k){\displaystyle \sum _{0\leq k<100}f(k)}

Сумма f(x){\displaystyle f(x)} элементов x{\displaystyle x} множества S{\displaystyle S}:

∑x∈⁡Sf(x){\displaystyle \sum _{x\mathop {\in } S}f(x)}

Сумма μ(d){\displaystyle \mu (d)} всех положительных чисел d{\displaystyle d}, являющихся делителями числа n{\displaystyle n}:

∑d|nμ(d){\displaystyle \sum _{d|n}\;\mu (d)}

Несколько символов сигма могут обобщать, например:

∑ℓ,ℓ′=∑ℓ∑ℓ′{\displaystyle \sum _{\ell ,\ell ‘}=\sum _{\ell }\sum _{\ell ‘}}

Бесконечная сумма[править | править код]

В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.

Примеры[править | править код]

1. Сумма арифметической прогрессии:

∑i=0n(a0+b⋅i)=(n+1)a0+an2{\displaystyle \sum _{i=0}^{n}(a_{0}+b\cdot i)=(n+1){\frac {a_{0}+a_{n}}{2}}}

---

2. Сумма геометрической прогрессии:

∑i=0na0⋅bi=a0⋅1−bn+11−b{\displaystyle \sum _{i=0}^{n}a_{0}\cdot b^{i}=a_{0}\cdot {\frac {1-b^{n+1}}{1-b}}}

---

3.∑k=1nk3=[n(n+1)2]2=(∑k=1nk)2{\displaystyle \sum \limits _{k=1}^{n}k^{3}=\left[{\frac {n(n+1)}{2}}\right]^{2}=\left(\sum \limits _{k=1}^{n}k\right)^{2}}

---

4. ∑i=0n(1p)i=pp−1(1−1pn+1),p≠1,n≥0{\displaystyle \sum _{i=0}^{n}{\left({\frac {1}{p}}\right)}^{i}={\frac {p}{p-1}}\left(1-{\frac {1}{p^{n+1}}}\right),\quad p\neq 1,n\geq 0}

Доказательство

∑i=0n(1p)i=∑i=0n1⋅1pi=1⋅1−(1p)n+11−1p=pn+1−1pn+1p−1p=pn+1−1pn(p−1)=pp−1(1−1pn+1){\displaystyle \sum _{i=0}^{n}{\left({\frac {1}{p}}\right)}^{i}=\sum _{i=0}^{n}{1\cdot {\frac {1}{p^{i}}}}=1\cdot {\frac {1-{\left({\frac {1}{p}}\right)}^{n+1}}{1-{\frac {1}{p}}}}={\frac {\frac {p^{n+1}-1}{p^{n+1}}}{\frac {p-1}{p}}}={\frac {p^{n+1}-1}{p^{n}(p-1)}}={\frac {p}{p-1}}\left(1-{\frac {1}{p^{n+1}}}\right)}

---

5. ∑i=0nipi=npn+2−(n+1)pn+1+p(p−1)2,p≠1{\displaystyle \sum _{i=0}^{n}ip^{i}={\frac {np^{n+2}-(n+1)p^{n+1}+p}{(p-1)^{2}}},\quad p\neq 1}

Доказательство

∑i=0nipi=∑i=1nipi=p⋅∑i=1nipi−1=p⋅∑i=0n−1(i+1)pi=p⋅(∑i=0n−1ipi+∑i=0n−1pi)=p⋅∑i=0nipi−p⋅npn+p⋅1−pn1−p⇒{\displaystyle \sum _{i=0}^{n}ip^{i}=\sum _{i=1}^{n}ip^{i}=p\cdot \sum _{i=1}^{n}ip^{i-1}=p\cdot \sum _{i=0}^{n-1}(i+1)p^{i}=p\cdot \left(\sum _{i=0}^{n-1}{ip^{i}}+\sum _{i=0}^{n-1}p^{i}\right)=p\cdot \sum _{i=0}^{n}ip^{i}-p\cdot np^{n}+p\cdot {\frac {1-p^{n}}{1-p}}\Rightarrow }

⇒(1−p)∑i=0nipi=−npn+1(1−p)+p−pn+11−p⇒∑i=0nipi=npn+2−(n+1)pn+1+p(1−p)2{\displaystyle \Rightarrow (1-p)\sum _{i=0}^{n}ip^{i}={\frac {-np^{n+1}(1-p)+p-p^{n+1}}{1-p}}\Rightarrow \sum _{i=0}^{n}ip^{i}={\frac {np^{n+2}-(n+1)p^{n+1}+p}{(1-p)^{2}}}}

---

6. ∑i=0npi=(p−1)∑i=0n−1((n−i)pi)+n+1,p≠1{\displaystyle \sum _{i=0}^{n}p^{i}=(p-1)\sum _{i=0}^{n-1}((n-i)p^{i})+n+1,\quad p\neq 1}

Доказательство

(p−1)∑i=0n−1((n−i)pi)+n+1=(p−1)∑i=0n((n−i)pi)+n+1=(p−1)(n⋅∑i=0npi−∑i=0nipi)+n+1={\displaystyle (p-1)\sum _{i=0}^{n-1}((n-i)p^{i})+n+1=(p-1)\sum _{i=0}^{n}((n-i)p^{i})+n+1=(p-1)\left(n\cdot \sum _{i=0}^{n}p^{i}-\sum _{i=0}^{n}ip^{i}\right)+n+1=}

=(p−1)(n⋅1−pn+11−p−npn+2−(n+1)pn+1+p(1−p)2)+n+1={\displaystyle =(p-1)\left(n\cdot {\frac {1-p^{n+1}}{1-p}}-{\frac {np^{n+2}-(n+1)p^{n+1}+p}{(1-p)^{2}}}\right)+n+1=}

=npn+2−np−npn+1+n−npn+2+npn+1+pn+1−p+pn−n+p−1p−1={\displaystyle ={\frac {np^{n+2}-np-np^{n+1}+n-np^{n+2}+np^{n+1}+p^{n+1}-p+pn-n+p-1}{p-1}}=}

=pn+1−1p−1=∑i=0npi{\displaystyle ={\frac {p^{n+1}-1}{p-1}}=\sum _{i=0}^{n}p^{i}}

Стоит заметить, что при p=10 {\displaystyle p=10\ } получаем ∑i=0n10i=9⋅∑i=0n−1((n−i)10i)+n+1{\displaystyle \sum _{i=0}^{n}10^{i}=9\cdot \sum _{i=0}^{n-1}((n-i)10^{i})+n+1}, а это последовательность равенств следующего вида:
1=9⋅0+1,11=9⋅1+2,111=9⋅12+3,1111=9⋅123+4,11111=9⋅1234+5{\displaystyle 1=9\cdot 0+1,\quad 11=9\cdot 1+2,\quad 111=9\cdot 12+3,\quad 1111=9\cdot 123+4,\quad 11111=9\cdot 1234+5}

Неопределённая сумма[править | править код]

Неопределённой суммой ai{\displaystyle a_{i}} по i{\displaystyle i} называется такая функция f(i){\displaystyle f(i)}, обозначаемая ∑iai{\displaystyle \sum _{i}^{}a_{i}}, что ∀i:f(i+1)−f(i)=ai{\displaystyle \forall i:f(i+1)-f(i)=a_{i}}.

Формула Ньютона — Лейбница[править | править код]

Если найдена неопределённая сумма ∑iai=f(i){\displaystyle \sum _{i}^{}a_{i}=f(i)}, то ∑i=abai=f(b+1)−f(a){\displaystyle \sum _{i=a}^{b}a_{i}=f(b+1)-f(a)}.

Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, появляется глагол «суммировать» (1489 год).

Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.

Специальный символ для обозначения суммы (S) первым ввёл Леонард Эйлер в 1755 году. Как вариант, использовалась греческая буква Сигма Σ. Позднее ввиду связи понятий суммирования и интегрирования, S также использовали для обозначения операции интегрирования.

В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ · ∑).

• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.

Таблиця математичних символів — Вікіпедія

Символ (TeX)	Символ (Unicode)	Назва	Значення	Приклад
		Вимова
		Розділ математики
⇒{\displaystyle \Rightarrow \,}	⇒	Імплікація, слідування	A⇒B{\displaystyle A\Rightarrow B\,} означає «коли A{\displaystyle A} істинне, то B{\displaystyle B} також істинне». Іноді використовують →{\displaystyle \rightarrow \,}.	x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4\,} істинне, але x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2\,} хибно (тому що x=−2{\displaystyle x=-2} також є розв’язком).
		«з… випливає» або «якщо…, то…»
		скрізь
⇔{\displaystyle \Leftrightarrow }	⇔, ↔	Рівносильність	A⇔B{\displaystyle A\Leftrightarrow B} означає «A{\displaystyle A} істинне тоді і тільки тоді, коли B{\displaystyle B} істинне».	x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y\,}
		«тоді і тільки тоді» або «рівносильно»
		скрізь
∧{\displaystyle \wedge }	∧	Кон’юнкція	A∧B{\displaystyle A\wedge B} істинне тоді і тільки тоді, коли A{\displaystyle A} і B{\displaystyle B} обидва істині.	(n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, якщо n{\displaystyle n} — натуральне число.
		«і»
		Математична логіка
∨{\displaystyle \vee }	∨	Диз’юнкція	A∨B{\displaystyle A\vee B} істинне, коли хоча б одна з умов A{\displaystyle A} або B{\displaystyle B} є істинною.	(n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, якщо n{\displaystyle n} — натуральне число.
		«або»
		Математична логіка
¬{\displaystyle \neg }	¬	Заперечення	¬A{\displaystyle \neg A} істинне тоді і тільки тоді, коли хибно A{\displaystyle A}.	¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)}
		«не»
		Математична логіка
∀{\displaystyle \forall }	∀	Квантор загальності	∀x,P(x){\displaystyle \forall x,P(x)} означає «P(x){\displaystyle P(x)} істинне для всіх x{\displaystyle x}».	∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n}
		«Для будь-яких», «Для всіх»
		Математична логіка
∃{\displaystyle \exists }	∃	Квантор існування	∃x,P(x){\displaystyle \exists x,\;P(x)} означає «існує хоча б одне x{\displaystyle x} таке, що P(x){\displaystyle P(x)} істинне»	∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (підходить число 5)
		«існує»
		Математична логіка
={\displaystyle =\,}	=	Рівність	x=y{\displaystyle x=y} означає «x{\displaystyle x} і y{\displaystyle y} означають один і той же об’єкт».	1 + 2 = 6 − 3
		«дорівнює»
		скрізь
:={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } =def{\displaystyle {\stackrel {\rm {def}}{=}}}	:= :⇔	Визначення	x:=y{\displaystyle x:=y} означає «x{\displaystyle x} за визначенням дорівнює y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означає «P{\displaystyle P} за визначенням рівносильно Q{\displaystyle Q}»	ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}(x):={1 \over 2}\left(e^{x}+e^{-x}\right)} (Гіперболічний косинус) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (Виключаюче або)
		«дорівнює/рівносильно за визначенням»
		скрізь
{,}{\displaystyle \{,\}}	{ , }	Множина елементів	{a,b,c}{\displaystyle \{a,\;b,\;c\}} означає множина, елементами якої є a{\displaystyle a}, b{\displaystyle b} та c{\displaystyle c}.	N={0,1,2,…}{\displaystyle \mathbb {N} =\{0,\;1,\;2,\;\ldots \}} (множина натуральних чисел)
		«Множина…»
		Теорія множин
{|}{\displaystyle \{|\}} {:}{\displaystyle \{:\}}	{ | } { : }	Множина елементів, що задовольняють умові	{x|P(x)}{\displaystyle \{x\,|\,P(x)\}} означає множину усіх x{\displaystyle x} таких, що істинне P(x){\displaystyle P(x)}.	{n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}}
		«Множина всіх… таких, що істинне…»
		Теорія множин
∅{\displaystyle \varnothing } {}{\displaystyle \{\}}	∅ {}	Порожня множина	{}{\displaystyle \{\}} і ∅{\displaystyle \varnothing } означає множину, що не містить жодного елементу.	{n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing }
		«Порожня множина»
		Теорія множин
∈{\displaystyle \in } ∉{\displaystyle \notin }	∈ ∉	приналежність/неприналежність до множини	a∈S{\displaystyle a\in S} означає «a{\displaystyle a} є елементом множини S{\displaystyle S}» a∉S{\displaystyle a\notin S} означає «a{\displaystyle a} не є елементом S{\displaystyle S}»	2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} }
		«належить», «з» «не належить»
		Теорія множин
⊆{\displaystyle \subseteq } ⊂{\displaystyle \subset }	⊆ ⊂	Підмножина	A⊆B{\displaystyle A\subseteq B} означає «кожний елемент з A{\displaystyle A} також є елементом з B{\displaystyle B}». A⊂B{\displaystyle A\subset B} як правило означає те ж, що і A⊆B{\displaystyle A\subseteq B}. Однак деякі автори використовують ⊂{\displaystyle \subset }, щоб показати строге включення (а саме ⊊{\displaystyle \subsetneq }).	(A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} }
		«є підмножиною», «включено в»
		Теорія множин
⊊{\displaystyle \subsetneq }	⫋	Власна підмножина	A⊊B{\displaystyle A\subsetneq B} означає A⊆B{\displaystyle A\subseteq B} і A≠B{\displaystyle A\neq B}.	N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} }
		«є власною підмножиною», «строго включається в»
		Теорія множин
∪{\displaystyle \cup }	∪	Об’єднання	A∪B{\displaystyle A\cup B} означає множину елементів, що належать A{\displaystyle A} або B{\displaystyle B} (або обом одразу).	A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B}
		«Об’єднання … і …», «…, об’єднане з …»
		Теорія множин
∩{\displaystyle \cap }	⋂	Перетин	A∩B{\displaystyle A\cap B} означає множину елементів, що належать і A{\displaystyle A}, і B{\displaystyle B}.	{x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}}
		«Перетин … і … », «…, перетнуте з …»
		Теорія множин
∖{\displaystyle \setminus }	\	Різниця множин	A∖B{\displaystyle A\setminus B} означає множину елементів, що належать A{\displaystyle A}, але не належать B{\displaystyle B}.	{1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}}
		«різниця … і … », «мінус», «… без …»
		Теорія множин
→{\displaystyle \to }	→	Функція	f:X→Y{\displaystyle f\!\!:X\to Y} означає функцію f{\displaystyle f}, що відображає множину (область визначення) X{\displaystyle X} у множину Y{\displaystyle Y}.	Функція f:Z→Z{\displaystyle f\!\!:\mathbb {Z} \to \mathbb {Z} }, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}}
		«з … в»,
		скрізь
↦{\displaystyle \mapsto }	↦	Відображення	x↦f(x){\displaystyle x\mapsto f(x)} означає, що образом x{\displaystyle x} після застосування функції f{\displaystyle f} буде f(x){\displaystyle f(x)}.	Функцію, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}}, можна записати так: f:x↦x2{\displaystyle f\colon x\mapsto x^{2}}
		«відображується в»
		скрізь
N{\displaystyle \mathbb {N} }	N або ℕ	Натуральні числа	N{\displaystyle \mathbb {N} } означає множину {1,2,3,…}{\displaystyle \{1,\;2,\;3,\;\ldots \}} або

Математические знаки и символы: список, таблица, история возникновения

Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.

Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.

В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.

Модели образования графических обозначений

На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».

Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения — это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.

История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.

Преобразование словесного представления

Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.

Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.

Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.

Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.

Назначение произвольного символа

Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны — знак обычно утверждается в результате рекомендации одного из членов научного сообщества.

Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.

Простейшие операции

Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.

Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.

Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).

Латинские буквы

На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).

Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.

Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.

Греческие буквы

В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.

Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.

Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.

Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.

Знаки логики

Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.

В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.

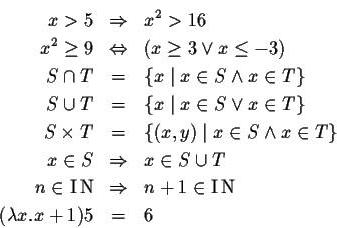Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.

Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.

Математические символы на английском

Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).

Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).

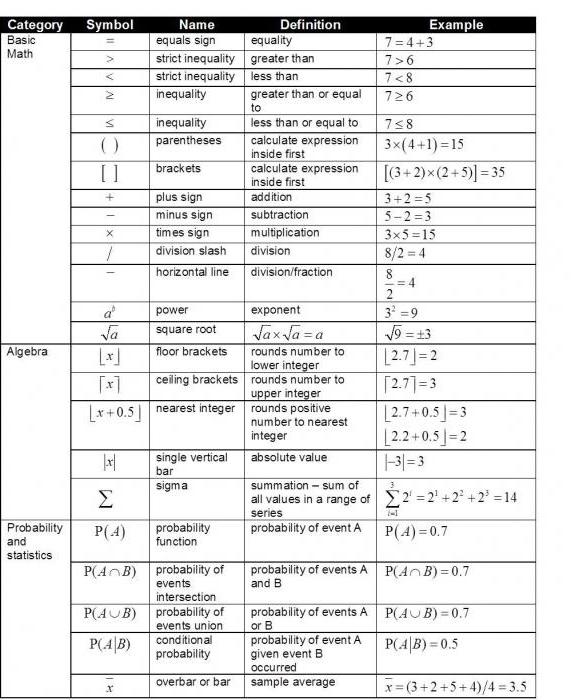
Таблица символов

Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.

Математические знаки в текстовом редакторе

При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.

Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.

В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.

Стоит ли учить математические символы

Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.

Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.

В заключение

Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.

Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.

Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.

Обсуждение:Таблица математических символов — Википедия

Материал из Википедии — свободной энциклопедии

Совершенно необходимо добавить колонку или строчку, где будет описано, как получить эти символы в ТеХе. Смотреть исходник — не вариант

Если вернусь из отпуска и не увижу, сделаю сам

Xtotdam (обс) 19:39, 10 июня 2016 (UTC)

Люди более опытные, посмотрите, пожалуйста: Участник:Xtotdam/Mathsymtable. Если все ОК, то стоит перенести и забыть. Xtotdam (обс.) 21:14, 6 ноября 2016 (UTC)

Хорошо. Может стоит перенести последнюю колонку сразу после первой? Или вообще их объединить? Как-то так:

— Алексей Копылов 06:52, 7 ноября 2016 (UTC)

Отличная идея, по крайней мере для большинства строк. Проблема в нижних строках, где производные сравнительно объемны по количеству кода Xtotdam (обс.) 13:23, 9 ноября 2016 (UTC)

Поправил, посмотрел: получается местами грязно и нехорошо; нижние строки, там, где ТеХовские выражения становятся объемными, вообще в левую колонку лучше не тащить. Я за первоначальный вариант с дополнительной колонкой справа. Отдельно, на мой взгляд, стоит оставить ТеХовые команды справа, как не самую важную, а скорее справочную информацию. Впрочем, переделать недолго 🙂 Xtotdam (обс.) 13:53, 9 ноября 2016 (UTC)

Вообще статья называется «Таблица математических символов». Поэтому должны быть только команды для символов, всякие \frac — не нужны. Для последних строчек можно только оставить (\partial), а остальные вообще оставить без TeXовских команд. Впрочем это дело вкуса, любой вариант приемлем. — Алексей Копылов 20:38, 9 ноября 2016 (UTC)

Предлагаю финальный вариант, компромиссный. Все тривиальные команды убраны, все остальные перенесены в левый столбец. Участник:Xtotdam/Mathsymtable Xtotdam (обс.) 20:45, 12 ноября 2016 (UTC)

Спасибо, мне нравится. — Алексей Копылов 23:43, 12 ноября 2016 (UTC)

Благодарю 🙂 Xtotdam (обс.) 11:10, 13 ноября 2016 (UTC)

Произносятся обычно буквы, слова. Знаки могут, например, обозначать, интерпретироваться, читаться, расшифровываться и т.п. Fractaler 13:55, 9 января 2010 (UTC)

Что случилось с таблицей? Теперь в двух левых столбцах вместо чисел и LaTeX-мнемоник отображаются сами символы в виде картинок. 89.232.105.12 02:08, 6 марта 2010 (UTC)

А никогда там команд и не было. Код можно посмотреть в исходнике. infovarius 19:54, 6 марта 2010 (UTC)

А как правильно записывать перечисление?[править код]

A={xi|i=1,2,3…n}{\displaystyle A=\{x_{i}|i=1,2,3…n\}}, как здесь?
A={xi|i=1..n}{\displaystyle A=\{x_{i}|i=1..n\}}, как здесь?
A={xi|i=1,…,n}{\displaystyle A=\{x_{i}|i=1,…,n\}}, как здесь?
Или A={xi|i∈{1,…,n}}{\displaystyle A=\{x_{i}|i\in \{1,…,n\}\}}?

Если все эти нотации верны, то является ли «..» математическим символом?—Piyavkin 08:11, 19 марта 2010 (UTC)

Не хватает такого символа в таблице. Обычно, видел такой при описании множеств, например, Grf={x,f(x)|a∈S{\displaystyle a\in S}} 178.120.151.144 17:42, 19 июля 2013 (UTC)

Добавьте норму, пожалуйста: ‖. В англвики она есть. Спасибо. 188.123.230.181 20:51, 3 июня 2014 (UTC)

Символов недостаточно[править код]

Почему так мало символов? Например, нет ≺ и ≼ — символов отношения порядка. Или нет квантора отрицания существования ∄. 217.9.87.108 19:28, 25 октября 2018 (UTC)

Знаки математические — Большая советская энциклопедия

Зна́ки математические

Условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. Например, √2

(квадратный корень из двух), 3 > 2 (три больше двух) и т.п.

Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первыми З. м. были знаки для изображения чисел — Цифры, возникновение которых, по-видимому, предшествовало письменности. Наиболее древние системы нумерации — вавилонская и египетская — появились ещё за 3¹/₂ тысячелетия до н. э.

Первые З. м. для произвольных величин появились много позднее (начиная с 5—4 вв. до н. э.) в Греции. Величины (площади, объёмы, углы) изображались в виде отрезков, а произведение двух произвольных однородных величин — в виде прямоугольника, построенного на соответствующих отрезках. В «Началах» Евклида (3 в. до н. э.) величины обозначаются двумя буквами — начальной и конечной буквами соответствующего отрезка, а иногда и одной. У Архимеда (3 в. до нашей эры) последний способ становится обычным. Подобное обозначение содержало в себе возможности развития буквенного исчисления. Однако в классической античной математике буквенного исчисления создано не было.

Начатки буквенного изображения и исчисления возникают в позднеэллинистическую эпоху в результате освобождения алгебры от геометрической формы. Диофант (вероятно, 3 в.) записывал неизвестную (х) и её степени следующими знаками:

[ — от греческого термина δυναμις (dynamis — сила), обозначавшего квадрат неизвестной, — от греческого χυβος (k_ybos) — куб]. Справа от неизвестной или её степеней Диофант писал коэффициенты, например 3х

5 изображалось

(где = 3). При сложении Диофант приписывал слагаемые друг к другу, для вычитания употреблял специальный знак ; равенство Диофант обозначал буквой ι [от греческого ισος (isos) — равный]. Например, уравнение

(x³ + 8x) — (5x² + 1) = х

у Диофанта записалось бы так:

(здесь

означает, что единица не имеет множителя в виде степени неизвестного).

Несколько веков спустя индийцы ввели различные З. м. для нескольких неизвестных (сокращения наименований цветов, обозначавших неизвестные), квадрата, квадратного корня, вычитаемого числа. Так, уравнение

3х² + 10x — 8 = x² + 1

в записи Брахмагупты (См. Брахмагупта) (7 в.) имело бы вид:

йа ва 3 йа 10 ру 8

йа ва 1 йа 0 ру 1

(йа — от йават — тават — неизвестное, ва — от варга — квадратное число, ру — от рупа — монета рупия — свободный член, точка над числом означает вычитаемое число).

Создание современной алгебраической символики относится к 14—17 вв.; оно определялось успехами практической арифметики и учения об уравнениях. В различных странах стихийно появляются З. м. для некоторых действий и для степеней неизвестной величины. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный символ. Так, в конце 15 и. Н. Шюке и Л. Пачоли употребляли знаки сложения и вычитания

(от лат. plus и minus), немецкие математики ввели современные + (вероятно, сокращение лат. et) и —. Ещё в 17 в. можно насчитать около десятка З. м. для действия умножения.

Различны были и З. м. неизвестной и её степеней. В 16 — начале 17 вв. конкурировало более десяти обозначений для одного только квадрата неизвестной, например се (от census — латинский термин, служивший переводом греческого δυναμις, Q (от quadratum),

, A (2), , Aii, aa, a² и др. Так, уравнение

x³ + 5x = 12

имело бы у итальянского математика Дж. Кардано (1545) вид:

у немецкого математика М. Штифеля (1544):

у итальянского математика Р. Бомбелли (1572):

французского математика Ф. Виета (1591):

у английского математика Т. Гарриота (1631):

В 16 и начале 17 вв. входят в употребление знаки равенства и скобки: квадратные (Р. Бомбелли, 1550), круглые (Н. Тарталья, 1556), фигурные (Ф. Виет, 1593). В 16 в. современный вид принимает запись дробей.

Значительным шагом вперёд в развитии математической символики явилось введение Виетом (1591) З. м. для произвольных постоянных величин в виде прописных согласных букв латинского алфавита В, D, что дало ему возможность впервые записывать алгебраические уравнения с произвольными коэффициентами и оперировать ими. Неизвестные Виет изображал гласными прописными буквами А, Е,… Например, запись Виета

[cubus — куб, planus — плоский, т. е. В — двумерная величина; solidus — телесный (трёхмерный), размерность отмечалась для того, чтобы все члены были однородны] в наших символах выглядит так:

x₃ + 3bx = d.

Виет явился творцом алгебраических формул. Р. Декарт (1637) придал знакам алгебры современный вид, обозначая неизвестные последними буквами лат. алфавита х, у, z, а произвольные данные величины — начальными буквами а, b, с. Ему же принадлежит нынешняя запись степени. Обозначения Декарта обладали большим преимуществом по сравнению со всеми предыдущими. Поэтому они скоро получили всеобщее признание.

Дальнейшее развитие З. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики которого основа была уже в большой мере подготовлена в алгебре.

Даты возникновения некоторых математических знаков

знак	значение	Кто ввёл	Когда введён
Знаки индивидуальных объектов
∞	бесконечность	Дж. Валлис	1655
e	основание натуральных логарифмов	Л. Эйлер	1736
π	отношение длины окружности к диаметру	У. Джонс Л. Эйлер	1706 1736
i	корень квадратный из -1	Л. Эйлер	1777 (в печати 1794)
i j k	единичные векторы, орты	У. Гамильтон	1853
П (а)	угол параллельности	Н.И. Лобачевский	1835
Знаки переменных объектов
x,y, z	неизвестные или переменные величины	Р. Декарт	1637
r	вектор	О. Коши	1853
Знаки индивидуальных операций
+	сложение	немецкие математики	Конец 15 в.
–	вычитание
×	умножение	У. Оутред	1631
․	умножение	Г. Лейбниц	1698
:	деление	Г. Лейбниц	1684
a2, a3,…, an	степени	Р. Декарт	1637
		И. Ньютон	1676
	корни	К. Рудольф	1525
		А. Жирар	1629
Log	логарифм	И. Кеплер	1624
log		Б. Кавальери	1632
sin	синус	Л. Эйлер	1748
cos	косинус
tg	тангенс	Л. Эйлер	1753
arc.sin	арксинус	Ж. Лагранж	1772
Sh	гиперболический синус	В. Риккати	1757
Ch	гиперболический косинус
dx, ddx, …	дифференциал	Г. Лейбниц	1675 (в печати
d2x, d3x,…		1684)
	интеграл	Г. Лейбниц	1675 (в печати 1686)
	производная	Г. Лейбниц	1675
ƒ’x	производная	Ж. Лагранж	1770, 1779
y’
ƒ'(x)
Δx	разность	Л. Эйлер	1755
	частная производная	А. Лежандр	1786
	определённый интеграл	Ж. Фурье	1819-22
Σ	сумма	Л. Эйлер	1755
П	произведение	К. Гаусс	1812
!	факториал	К. Крамп	1808
	x		модуль	К. Вейерштрасс	1841
lim	предел	У. Гамильтон,	1853,
lim	многие математики	начало 20 в.
n = ∞
lim
n → ∞
ξ	дзета-функция	Б. Риман	1857
Г	гамма-функция	А. Лежандр	1808
В	бета-функция	Ж. Бине	1839
Δ	дельта (оператор Лапласа)	Р. Мёрфи	1833
∇	набла (оператор Гамильтона)	У. Гамильтон	1853
Знаки переменных операций
φx	функция	И. Бернули	1718
f (x)		Л. Эйлер	1734
Знаки индивидуальных отношений
=	равенство	Р. Рекорд	1557
>	больше	Т. Гарриот	1631
<	меньше
≡	сравнимость	К. Гаусс	1801
			параллельность	У. Оутред	1677
⊥	перпендикулярность	П. Эригон	1634

И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) величины (в виде

и для бесконечно малого приращения o. Несколько ранее Дж. Валлис (1655) предложил знак бесконечности ∞.

Создателем современной символики дифференциального и интегрального исчислений является Г. Лейбниц. Ему, в частности, принадлежат употребляемые ныне З. м. дифференциалов

dx, d ²x, d ³x

и интеграла

Огромная заслуга в создании символики современной математики принадлежат Л. Эйлеру. Он ввёл (1734) в общее употребление первый знак переменной операции, именно знак функции f (x) (от лат. functio). После работ Эйлера знаки для многих индивидуальных функций, например тригонометрических, приобрели стандартный характер. Эйлеру же принадлежат обозначения постоянных е (основание натуральных логарифмов, 1736), π [вероятно, от греческого περιφερεια (periphereia) — окружность, периферия, 1736], мнимой единицы

(от французского imaginaire — мнимый, 1777, опубликовано в 1794).

В 19 в. роль символики возрастает. В это время появляются знаки абсолютной величины |x| (К. Вейерштрасс, 1841), вектора r̅ (О. Коши, 1853), определителя

(А. Кэли, 1841) и др. Многие теории, возникшие в 19 в., например Тензорное исчисление, не могли быть развиты без подходящей символики.

Наряду с указанным процессом стандартизации З. м. в современной литературе весьма часто можно встретить З. м., используемые отдельными авторами только в пределах данного исследования.

С точки зрения математической логики, среди З. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений. Например, знаки 1, 2, 3, 4 изображают числа, т. е. объекты, изучаемые арифметикой. Знак операции сложения + сам по себе не изображает никакого объекта; он получает предметное содержание, когда указано, какие числа складываются: запись 1 + 3 изображает число 4. Знак > (больше) есть знак отношения между числами. Знак отношения получает вполне определённое содержание, когда указано, между какими объектами отношение рассматривается. К перечисленным трём основным группам З. м. примыкает четвёртая: Г) вспомогательные знаки, устанавливающие порядок сочетания основных знаков. Достаточное представление о таких знаках дают скобки, указывающие порядок производства действий.

Знаки каждой из трёх групп А), Б) и В) бывают двух родов: 1) индивидуальные знаки вполне определённых объектов, операций и отношений, 2) общие знаки «неременных», или «неизвестных», объектов, операций и отношений.

Примеры знаков первого рода могут служить (см. также таблицу):

A₁) Обозначения натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9; трансцендентных чисел е и π; мнимой единицы i.

Б₁) Знаки арифметических действий +, —, ·, ×,:; извлечения корня , дифференцирования

знаки суммы (объединения) ∪ и произведения (пересечения) ∩ множеств; сюда же относятся знаки индивидуальных функций sin, tg, log и т.п.

B₁) Знаки равенства и неравенства =, >, <, ≠, знаки параллельности || и перпендикулярности ⊥, знаки принадлежности ∈ элемента некоторому множеству и включения ⊂ одного множества в другое и т.п.

Знаки второго рода изображают произвольные объекты, операции и отношения определённого класса или объекты, операции и отношения, подчинённые каким-либо заранее оговорённым условиям. Например, при записи тождества (a + b)(a — b) = a²— b² буквы а и b обозначают произвольные числа; при изучения функциональной зависимости у = х² буквы х и у — произвольные числа, связанные заданным отношением; при решении уравнения

x² — 1 = 0

х обозначает любое число, удовлетворяющее данному уравнению (в результате решения этого уравнения мы узнаём, что этому условию соответствуют лишь два возможных значения +1 и —1).

С логической точки зрения, законно такого рода общие знаки называть знаками переменных, как это принято в математической логике, не пугаясь того обстоятельства, что «область изменения» переменного может оказаться состоящей из одного единственного объекта или даже «пустой» (например, в случае уравнений, не имеющих решения). Дальнейшими примерами такого рода знаков могут служить:

A₂) Обозначения точек, прямых, плоскостей и более сложных геометрических фигур буквами в геометрии.

Б₂) Обозначения f, F, φ для функций и обозначения операторного исчисления, когда одной буквой L изображают, например, произвольный оператор вида:

Обозначения для «переменных отношений» менее распространены, они находят применение лишь в математической логике (см. Алгебра логики) и в сравнительно абстрактных, по преимуществу аксиоматических, математических исследованиях.

Лит.: Cajori F., A history of mathematical notations, v. 1—2, Chi., 1928—29.

Источник: Большая советская энциклопедия на Gufo.me

---

Значения в других словарях

1. ЗНАКИ МАТЕМАТИЧЕСКИЕ — ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок. Напр., математические знаки +, -, =, > (больше) — (знак корня) — sin (синус) — (интеграл) и т. Большой энциклопедический словарь
2. Знаки Математические — Условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие «квадратный корень из числа… Математическая энциклопедия

Символ бесконечности — Википедия

Материал из Википедии — свободной энциклопедии

Варианты написания символа бесконечности Символ со сходным начертанием: ထ

Символ бесконечности (∞) — математический символ, представляющий концепцию бесконечности.

Английский математик Джон Валлис, который ввёл символ бесконечности в математическую литературу Символ, использованный Эйлером для обозначения бесконечности

Введение символа бесконечности в математическом смысле в его современном виде принадлежит английскому математику Валлису, который впервые использовал этот символ в своём трактате 1655 года «О конических сечениях» (лат. De sectionibus conicis)^[1][2][3][4]. В своей книге Валлис никак не объяснил выбор этого символа для обозначения бесконечности, по некоторым предположениям, это мог быть вариант записи числа 1000 римскими цифрами (первоначально выглядевшей как CIƆ, либо CƆ), или буквы омега (ω) — последней буквы греческого алфавита^[5].

Леонард Эйлер использовал особый, открытый вариант символа бесконечности^[6] для того, чтобы обозначить «абсолютную бесконечность» (лат. absolutus infinitus). Этот символ бесконечности впоследствии никем не использовался и не представлен в Юникоде.

Символ долговечной бумаги в переплётном деле

В математике символ бесконечности используется чаще всего для выражения потенциальной бесконечности^[2], а не обозначения каких-то реальных бесконечно больших величин. Например, в математическом обозначении предела:

∑i=0∞12i=limx→∞2x−12x−1=2{\displaystyle \sum _{i=0}^{\infty }{\frac {1}{2^{i}}}=\lim _{x\to \infty }{\frac {2^{x}-1}{2^{x-1}}}=2},

знак бесконечности можно условно интерпретировать в том смысле, что переменная достигает сколь угодно больших значений (стремится к бесконечности), но не принимает значения, равного бесконечности.

В топологии символом бесконечности обозначается дополнительная точка, которая вводится при одноточечной компактификации Александрова. Аналогично, в комплексном анализе и проективной геометрии символ ∞{\displaystyle \infty } обозначает бесконечно удалённую точку.

Но в областях математики, в которых возникает необходимость сравнивать и различать между различными типами бесконечности, для конкретных бесконечных величин вместо символа ∞{\displaystyle \infty } используются иные обозначения. Например, в теории множеств, бесконечное кардинальное число множества натуральных чисел (мощность множества всех натуральных чисел) обозначается символом ℵ0{\displaystyle \aleph _{0}} (читается «алеф-нуль»), бесконечное кардинальное число множества счётных порядковых чисел обозначается ℵ1{\displaystyle \aleph _{1}}, при этом ℵ0<ℵ1{\displaystyle \aleph _{0}<\aleph _{1}}. См. Иерархия алефов.

В других отраслях символ бесконечности может иметь другой смысл; например, в переплётном деле он используется для указания, что книга напечатана на долговечной бумаге^[7].

В современной мистике символ бесконечности нередко отождествляется с образом Уробороса — змеи, поедающей собственный хвост^[8].

Владимир Набоков в таких своих произведениях, как «Дар» и «Бледный огонь», использует символический образ восьмёрки (в частности, в виде ленты Мёбиуса и символа бесконечности) в описаниях форм велосипедных шин и очертаний полузабытых людей. В поэме «Бледный огонь» упоминается, например «чудо лемнискаты»^[9].

Флаг метисов 1816 года

Символ бесконечности в настоящее время стал популярным элементом графического дизайна. Например, это изображение является основным на флаге канадских метисов, под которым сторонники Северо-западной компании выступили в сражении у семи дубов (англ.)русск. 1816 года^[10].

Многие современные крупные компании используют символ бесконечности в своих корпоративных логотипах, в частности, Infiniti, Room for PlayStation Portable (англ.)русск., Microsoft Visual Studio, CoorsTek (англ.)русск. и другие.

В Юникоде бесконечность обозначена символом ∞ (U+221E), в макропакете LaTeX как ∞{\displaystyle \infty } (\infty), имеются также другие варианты кодировки^[11].

1. ↑ De sectionibus conicis nova methodo expositis tractatus — John Wallis — Google Boeken (неопр.). Books.google.com. Дата обращения 1 декабря 2013.
2. ↑ ^{1 2} Barrow, John D. (2008), «Infinity: Where God Divides by Zero», Cosmic Imagery: Key Images in the History of Science, W. W. Norton & Company, с. 339–340, ISBN 9780393061772, <https://books.google.com/books?id=uRg6iN10JCIC&pg=PA339> 
3. ↑ Scott, Joseph Frederick (1981), The mathematical work of John Wallis, D.D., F.R.S., (1616-1703) (2 ed.), American Mathematical Society, с. 24, ISBN 0-8284-0314-7, <https://books.google.com/books?id=XX9PKytw8g8C&pg=PA24> 
4. ↑ Martin-Löf, Per (1990), «Mathematics of infinity», COLOG-88 (Tallinn, 1988), vol. 417, Lecture Notes in Computer Science, Berlin: Springer, с. 146–197, DOI 10.1007/3-540-52335-9_54 
5. ↑ Clegg, Brian (2003), A brief history of infinity: the quest to think the unthinkable, Robinson, ISBN 9781841196503 
6. ↑ See for instance Cor. 1 p. 174 in: Leonhard Euler. Variae observationes circa series infinitas. Commentarii academiae scientiarum Petropolitanae 9, 1744, pp. 160—188. [1]
7. ↑ Zboray, Ronald J. & Zboray, Mary Saracino (2000), A handbook for the study of book history in the United States, Center for the Book, Library of Congress, с. 49, ISBN 9780844410159 
8. ↑ O’Flaherty, Wendy Doniger (1986), Dreams, Illusion, and Other Realities, University of Chicago Press, с. 243, ISBN 9780226618555, <https://books.google.com/books?id=vhNNrX3bmo4C&pg=PA243> . The book also features this image on its cover.
9. ↑ Toker, Leona (1989), Nabokov: The Mystery of Literary Structures, Cornell University Press, с. 159, ISBN 9780801422119, <https://books.google.com/books?id=Jud1q_NrqpcC&pg=PA159> 
10. ↑ Healy, Donald T. & Orenski, Peter J. (2003), Native American Flags, University of Oklahoma Press, с. 284, ISBN 978-0-8061-3556-4 
11. ↑ Unicode chart (odf) (неопр.) (PDF). Дата обращения 1 декабря 2013.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Вставка математических знаков — Word

Основные математические символы	Нет	Часто используемые математические символы, такие как > и <
Греческие буквы	Строчные буквы	Строчные буквы греческого алфавита
	Прописные буквы	Прописные буквы греческого алфавита
Буквоподобные символы	Нет	Символы, которые напоминают буквы
Операторы	Обычные бинарные операторы	Символы, обозначающие действия над двумя числами, например + и ÷
	Обычные реляционные операторы	Символы, обозначающие отношение между двумя выражениями, такие как = и ~
	Основные N-арные операторы	Операторы, осуществляющие действия над несколькими переменными
	Сложные бинарные операторы	Дополнительные символы, обозначающие действия над двумя числами
	Сложные реляционные операторы	Дополнительные символы, обозначающие отношение между двумя выражениями
Стрелки	Нет	Символы, указывающие направление
Отношения с отрицанием	Нет	Символы, обозначающие отрицание отношения
Наборы знаков	Наборы знаков	Математический шрифт Script
	Готические	Математический шрифт Fraktur
	В два прохода	Математический шрифт с двойным зачеркиванием
Геометрия	Нет	Часто используемые геометрические символы