| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно.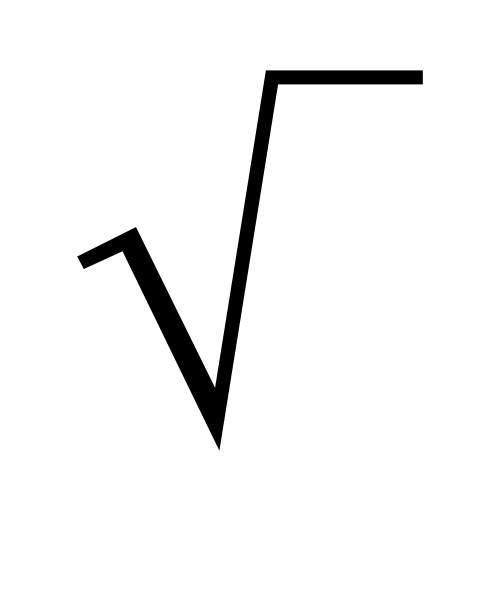 | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и .  Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
Таблица математических знаков (символов): значения, распечатать
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Основные математические знаки и символы
Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.
знак
т.е. 4 плюс 3 равно 7
7 не равно 10
0,35765 прибл. равно 0,36
15 больше 10
6 меньше 8
10 больше или равно 4
3 меньше или равно 7
7 : 2 = 3 (остаток 1)
microexcel.ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Кто придумал значок.
 Происхождение математических знаков. Проект по математике
Происхождение математических знаков. Проект по математикеОписание презентации по отдельным слайдам:
1 слайд
Описание слайда:
История происхождения математических знаков Подготовил: Черепанов Иван, ученик 5 В класс Учитель математики: Мосунова О.А. Как нет на свете без ножек столов, Как нет на свете без рожек козлов, Котов без усов и без панцирей раков, Так нет в арифметике действий без знаков!
2 слайд
Описание слайда:
3 слайд
Описание слайда:
Задачи Рассмотреть откуда математические знаки пришли к нам и что они изначально обозначали. Сравнить математические знаки разных народов. Рассмотреть сходство современных математических знаков со знаками наших предков
4 слайд
Описание слайда:
Объект: математические знаки разных народов Основные методы исследования: анализ литературы, сравнение, опрос учащихся, анализ и обобщение полученных в ходе исследования данных.
5 слайд
Описание слайда:
Почему в наше время мы используем именно такие математические знаки: + «плюс»,- « минус», ∙ « умножение» и: « деление», а не какие нибудь другие? Проблема
6 слайд
Описание слайда:
Гипотеза Я думаю, что математические знаки возникли одновременно с появлением цифр и чисел
7 слайд
Описание слайда:
Происхождение математических знаков Происхождение этих знаков не всегда можно точно установить. Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Существует мнение, что знаки «+» и «–» возникли в торговой практике. Виноторговец чёрточками отмечал, сколько мер вина он продал из бочки. Приливая в бочку новые запасы, он перечёркивал столько расходных чёрточек, сколько мер он восстановил. Так, якобы, произошли знаки сложения и вычитания в ХV веке. Относительно происхождения знака «+» существует и другое объяснение. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» («и») приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая, в конце концов, превратилась в знак «+»
Виноторговец чёрточками отмечал, сколько мер вина он продал из бочки. Приливая в бочку новые запасы, он перечёркивал столько расходных чёрточек, сколько мер он восстановил. Так, якобы, произошли знаки сложения и вычитания в ХV веке. Относительно происхождения знака «+» существует и другое объяснение. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» («и») приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая, в конце концов, превратилась в знак «+»
8 слайд
Описание слайда:
Алгебраического знак “- ” Первое использование современного алгебраического знака “ +” относится к немецкой рукописи по алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: + и — . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака + и — (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
9 слайд
Описание слайда:
Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест “†’’, иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид Видман
10 слайд
Описание слайда:
Первое появление « +» и «-» на английском языке обнаружено в книге по алгебре 1551 г. “The Whetstone of Witte” математика из Оксфорда Роберта Рекорда, который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак.![]() В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется «+» и обозначает больше, а второй «-» и обозначает меньше’’.
В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется «+» и обозначает больше, а второй «-» и обозначает меньше’’.
11 слайд
Описание слайда:
Знак вычитания Обозначения вычитания были несколько менее причудливыми, но, возможно, более запутанными (для нас, по крайней мере), так как вместо простого знака “- ” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Галлей и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
12 слайд
Описание слайда:
В Древней Египте В знаменитом египетском папирусе Ахмеса пара ног, идущих вперед, обозначает сложение, а уходящих — вычитание
13 слайд
Описание слайда:
Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полу-эллиптическую кривую для вычитания Индусы, как и греки, обычно никак не обозначали сложение, кроме того, что символы “yu’’ были использованы в рукописи Бахшали “Арифметика’’ (вероятно, это третий или четвертый век).![]()
14 слайд
Описание слайда:
В конце пятнадцатого века французский математик Шюке (1484 г.) и итальянский Пачоли (1494 г.) использовали “p ’’ (обозначая “плюс’’) для сложения “ m’’ (обозначая “минус’’) для вычитания. Шюке
15 слайд
Описание слайда:
В Италии В Италии символы «+» и «-» были приняты астрономом Кристофером Клавиусом (немцем, жившим в Риме), математиками Глориози и Кавальери в начале семнадцатого века Кристофер Клавиус
16 слайд
Описание слайда:
Знак умножения Для обозначения действия умножения одни из европейских математиков XVI века употребляли букву М, которая была начальной в латинском слове, обозначающем увеличение, умножение, – мультипликация (от этого слова произошло название «мультфильм»). В XVII веке некоторые математики стали обозначать умножение косым крестиком «×», а иные употребляли для этого точку. В Европе продолжительное время произведение называли суммой умножения. Название «множитель» упоминается в работах XI века. На протяжении тысячелетий действие деление не обозначали знаками. Арабы ввели для обозначения деления черту «/». Её перенял от арабов в XIII веке итальянский математик Фибоначчи. Он же первым употребил термин «частное». Знак двоеточия «:» для обозначения деления вошёл в употребление в конце XVII века. В России названия «делимое», «делитель», «частное» впервые ввёл Л.Ф. Магницкий в начале XVIII века. Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621).
Название «множитель» упоминается в работах XI века. На протяжении тысячелетий действие деление не обозначали знаками. Арабы ввели для обозначения деления черту «/». Её перенял от арабов в XIII веке итальянский математик Фибоначчи. Он же первым употребил термин «частное». Знак двоеточия «:» для обозначения деления вошёл в употребление в конце XVII века. В России названия «делимое», «делитель», «частное» впервые ввёл Л.Ф. Магницкий в начале XVIII века. Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621).
17 слайд
Описание слайда:
Знаки деления Отред предпочитал косую черту «/». Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл (John Pell) в середине XVII века.
В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл (John Pell) в середине XVII века.
18 слайд
Описание слайда:
Знаки равенства и неравенства Знак равенства обозначался в разные времена по-разному: и словами, и различными символами. Знак «=», столь удобный и понятный сейчас, вошёл во всеобщее употребление только в XVIII веке. А предложил этот знак для обозначения равенства двух выражений английский автор учебника алгебры Роберт Рикорд в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. Знак «не равно» впервые встречается у Эйлера. Знаки сравнения ввёл Томас Гарриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше.
Этот символ знаком любому пользователю интернета. Но появился он отнюдь не в век всеобщей компьютерной грамотности, символ который мы называем «собака» был известен еще в средние века, и у него было несколько разных назначений. Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.
Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.
Символ @ известен как минимум с XV века , но вполне возможно, что он был придуман и раньше. До сих пор доподлинно не установлено, как и откуда он появился, и время первого упоминания определено лишь приблизительно. По одной из версий, знак @ первыми стали использовать в письме монахи, делавшие переводы трактатов, которые были написаны в том числе и на латыни. В латыни есть предлог «ad», и в шрифте принятом в то время для письма, буква «d» писалась с небольшим хвостиком, закрученным вверх. При быстром письме предлог выглядел как значок @.
Благодаря флорентийским купцам, с XV века значок @ стал использоваться в качестве коммерческого символа. Он обозначал меру веса, равную 12,5 кг. – амфору, и по тогдашней традиции буква «А», которой и обозначался вес, была украшена завитками и выглядела как всем известный сегодня символ. У испанцев, португальцев и французов своя версия происхождения обозначения – от слова «арроба» — староиспанской меры веса около 15 кг, которую обозначали в письме условным знаком @, тоже взятом от первой буквы слова.
В современном коммерческом языке официальное название знака @ — «коммерческое at» произошло из бухгалтерских счетов, где обозначало предлог «в, на, по, к», и в русском переводе выглядело примерно так – 5шт. по 3$ (5 widgets @ $3 each). Так как символ использовался в торговле, то он был размещен на клавиатурах первых пишущих машинок, откуда и перебрался на компьютерную клавиатуру.
В интернете символ @ появился благодаря создателю электронной почты Томлинсону. Почему он выбрал этот знак для разделения имени пользователя и сервера электронной почты Томлинсон объяснил просто – он искал знак, который бы не встречался ни в именах, ни в названиях и не мог внести путаницу в систему. В разных странах символ называют по-разному, как собачка он известен лишь в русском языке. Версий появления этого забавного названия несколько. Согласно одной из них – звучание английского «at» напоминает собачий лай, по другой – сам значок напоминает свернувшуюся калачиком маленькую собачку. Но самая популярная связана с одной из первых текстовых игр.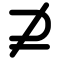 По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @.
По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @.
Кстати, символ @ во многих странах так или иначе пользователи связывают с животными – у немцев и поляков это обезьянка, у итальянцев – улитка, в Америке и Финляндии – кошка, на Тайване и в Китае – мышка. В других странах символ означает что-то вкусное – булочку с корицей у шведов, штрудель у израильтян. Только дисциплинированные японцы далеки от романтичных сравнений и предпочитают называть знак «attomark», так как он звучит в английском языке, и не придумывают для него своих названий.
Первое использование знаков + и — в печати в Behëde und Johannes Widman auff allen Kauffmanschafft, Аугсбург, 1526 г.
Марио Ливио
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928–1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930).
В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928–1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930).
Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полу-эллиптическую кривую для вычитания. В знаменитом египетском папирусе Ахмеса пара ног, идущих вперед, обозначает сложение, а уходящих — вычитание. Индусы, как и греки, обычно никак не обозначали сложение, кроме того, что символы “yu’’ были использованы в рукописи Бахшали “Арифметика’’ (вероятно, это третий или четвертый век).![]() В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
Несколько сомнительно, но считается, что наш знак происходит от одной из форм слова “et’’, которое значит “и’’ по-латыни. Первым человеком, который, возможно, использовал знак как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века. Рукопись 1417 г. также содержит символ (хотя палочка, направленная сверху вниз, не совсем вертикальна). И это тоже потомок одной из форм et.
Происхождение знака “” гораздо менее ясно, и высказываются гипотезы его появления от иероглифического письма или александрийской грамматики, до черты, которую использовали торговцы, чтобы отделить тару от общей массы товаров.
Первое использование современного алгебраического знака “” относится к немецкой рукописи по алгебре 1481 г. , которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: и . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
, которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: и . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
В Италии символы и были приняты астрономом Кристофером Клавиусом (немцем, жившим в Риме), математиками Глориози и Кавальери в начале семнадцатого века.
Первое появление и на английском языке обнаружено в книге по алгебре 1551 г. “The Whetstone of Witte” математика из Оксфорда , который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак . В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется и обозначает больше, а второй и обозначает меньше’’.
В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется и обозначает больше, а второй и обозначает меньше’’.
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест “†’’, иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид “’’.
Обозначения вычитания были несколько менее причудливыми, но, возможно, более запутанными (для нас, по крайней мере), так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
В общем, самым впечатляющим в этой истории является то, что символы, которые впервые появились в печати лишь около пятисот лет назад, стали частью того, что является, видимо, наиболее универсальным “языком’’. Занимаетесь ли вы наукой или финансами, живете в Кентукки или в Сибири, все равно вы точно знаете, что означают эти символы.
От индийских значков, показанных в нижней строке (начертание I века н. э.), произошли современные цифры
Для обозначения цифр от 1 до 9 в Индии с VI века до н. э. использовалось написание «брахми», с отдельными знаками для каждой цифры. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими , а сами арабы — индийскими .
Десятичная запятая, отделяющая дробную часть числа от целой, введена итальянским астрономом Маджини (1592) и Непером (1617).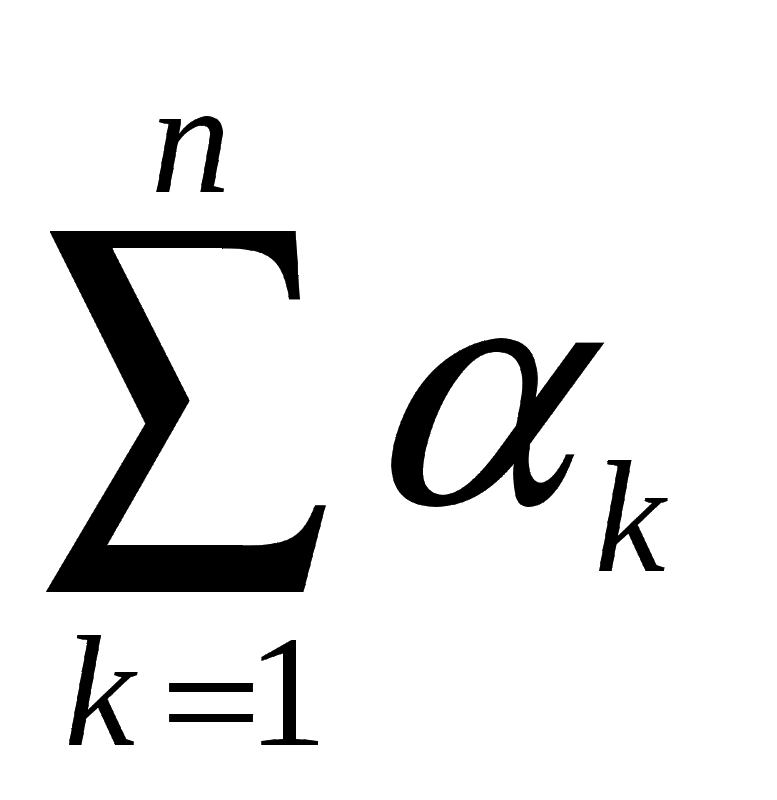 Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62
Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62
«Двухэтажная» запись обыкновенной дроби (например ) использовалась ещёдревнегреческими математиками, хотя знаменатель у них записывался надчислителем, а черты дроби не было. Индийские математики переместили числитель наверх; через арабов этот формат переняли в Европе. Дробную черту впервые в Европе ввёл Леонардо Пизанский (1202), но в обиход она вошла только при поддержке Иоганна Видмана (1489).
Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в учебнике Иоганна Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus)
Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали чаще всего букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран,1659). Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Знаки деления. Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц.
Знак плюс-минус появился у Жирара (1626) и Отреда. Правда, Жирар между плюсом и минусом писал ещё словами «или».
Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2.
Знак суммы ввёл Эйлер в 1755 году.
Знак произведения ввёл Гаусс в 1812 году.
Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).
Обозначение абсолютной величины и модуля комплексного числа появились уВейерштрасса в 1841 году. В 1903 году Лоренц использовал эту же символику для длины вектора.
=
Первое печатное появление знака равенства (записано уравнение )
Знак равенства предложил Роберт Рекорд в1557 году
Знак «приблизительно равно» придумал немецкий математик С. Гюнтер в 1882 году.
Гюнтер в 1882 году.
Знак «не равно» впервые встречается у Эйлера.
Автор знака «тождественно равно» — Бернхард Риман (1857). Этот же символ, по предложению Гаусса, используется в теории чисел как знак сравнения по модулю, а в логике — как знак операции эквивалентности.
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше , меньше .
Символы нестрогого сравнения предложил Валлис в 1670 году.
Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ угла у Эригона напоминал значок , современную форму ему придал Уильям Отред (1657).
Современные обозначения угловых единиц (градусы, минуты, секунды) встречаются ещё в «Альмагесте» Птолемея.
Радианную меру углов, более удобную для
анализа
, предложил в 1714 году английский математик
Роджер Котс
. Сам термин радиан придумал в 1873 году Джеймс Томсон, брат известного физика
лорда Кельвина
.
Общепринятое обозначение числа 3,14159… впервые образовал Уильям Джонс в1706 году, взяв первую букву слов греч. περιφρεια — окружность и περμετρος —периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.
Сокращённые обозначения для синуса и косинуса ввёл Отред в середине XVII века.
Сокращённые обозначения тангенса и котангенса: введены Иоганном Бернулли в XVIII веке, они получили распространение в Германии и России. В других странах употребляются названия этих функций , предложенные Альбером Жираром ещё ранее, в начале XVII века.
Манера обозначать обратные тригонометрических функции с помощью приставки arc (от лат. arcus , дуга) появилась у австрийского математика Карла Шерфера (нем. Karl Scherffer ; 1716—1783) и закрепилась благодаряЛагранжу. Имелось в виду, что, например, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу.![]() Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились.
Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились.
Символ частной производной сделали общеупотребительным сначала Карл Якоби (1837), а затем Вейерштрасс, хотя это обозначение уже встречалось ранее в одной работе Лежандра (1786).
Символ предела появился в 1787 году у Симона Люилье и получил поддержку Коши (1821) . Предельное значение аргумента сначала указывалось отдельно, после символа lim , а не под ним. Близкое к современному обозначение ввёл Вейерштрасс, однако вместо привычной нам стрелки он использовал знак равенства . Стрелка появилась в начале XX века сразу у нескольких математиков — например, у Харди (1908).
Символ этого дифференциального оператора придумал Уильям Роуэн Гамильтон(1853), а название «набла» предложил Хевисайд (1892).
находящейся на интернете в свободном доступе
http://goo.gl/WcU0Ss
Всем привычный значок @ не был известен в нашей стране до наступления компьютерной эры. Обычно при заимствовании названия из другого языка новое не изобретается, а просто копируется (так в русский язык пришли слова «почта» и «табак», а слова «водка» и «спутник» пересекли границу в обратном направлении). Но иногда исходное название может оказаться непроизносимым, неприличным или не соответствующим правилам языка. Видимо, это и произошло с символом @ — его официальное название «коммерческое эт» русскому уху кажется совершенно бессмысленным. Название должно быть таким, чтобы его хотелось запомнить и применять. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли, а «собака» распространилась по всему Рунету и осталась, потому что любой язык стремится иметь только одно универсальное слово для обозначения чего бы то ни было. Остальные названия остаются маргинальными, хотя их может быть очень много. Например, в английском языке символ @ называют не только словами commercial at, но и mercantile symbol, commercial symbol, scroll, arobase, each, about и т.
Обычно при заимствовании названия из другого языка новое не изобретается, а просто копируется (так в русский язык пришли слова «почта» и «табак», а слова «водка» и «спутник» пересекли границу в обратном направлении). Но иногда исходное название может оказаться непроизносимым, неприличным или не соответствующим правилам языка. Видимо, это и произошло с символом @ — его официальное название «коммерческое эт» русскому уху кажется совершенно бессмысленным. Название должно быть таким, чтобы его хотелось запомнить и применять. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли, а «собака» распространилась по всему Рунету и осталась, потому что любой язык стремится иметь только одно универсальное слово для обозначения чего бы то ни было. Остальные названия остаются маргинальными, хотя их может быть очень много. Например, в английском языке символ @ называют не только словами commercial at, но и mercantile symbol, commercial symbol, scroll, arobase, each, about и т.![]() д. Откуда взялась ассоциация между главным компьютерным значком и другом человека? Для многих символ @ действительно напоминает свернувшуюся калачиком собаку. Существует экзотическая версия, что отрывистое произношение английского at может напомнить собачий лай. Однако гораздо более вероятная гипотеза связывает наш символ с очень старой компьютерной игрой Adventure. В ней нужно было путешествовать по лабиринту, сражаясь с разными малоприятными подземными тварями. Поскольку игра была текстовая, сам игрок, стены лабиринта, монстры и клады обозначались различными символами (скажем, стены были постоены из «!», «+» и «-»). Игрока в Adventure сопровождал пес, которого можно было посылать с разведывательными миссиями. Обозначался он символом @. Возможно, именно благодаря этой ныне забытой компьютерной игре в России укоренилось название «собака». В современном мире знак @ присутствует повсюду, особенно с того момента, как он стал неотъемлемой частью адреса электронной почты. Но этот символ задолго до компьютерной эры входил в раскладку стандартной американской пишущей машинки, а компьютерным стал лишь потому, что сравнительно мало использовался.
д. Откуда взялась ассоциация между главным компьютерным значком и другом человека? Для многих символ @ действительно напоминает свернувшуюся калачиком собаку. Существует экзотическая версия, что отрывистое произношение английского at может напомнить собачий лай. Однако гораздо более вероятная гипотеза связывает наш символ с очень старой компьютерной игрой Adventure. В ней нужно было путешествовать по лабиринту, сражаясь с разными малоприятными подземными тварями. Поскольку игра была текстовая, сам игрок, стены лабиринта, монстры и клады обозначались различными символами (скажем, стены были постоены из «!», «+» и «-»). Игрока в Adventure сопровождал пес, которого можно было посылать с разведывательными миссиями. Обозначался он символом @. Возможно, именно благодаря этой ныне забытой компьютерной игре в России укоренилось название «собака». В современном мире знак @ присутствует повсюду, особенно с того момента, как он стал неотъемлемой частью адреса электронной почты. Но этот символ задолго до компьютерной эры входил в раскладку стандартной американской пишущей машинки, а компьютерным стал лишь потому, что сравнительно мало использовался.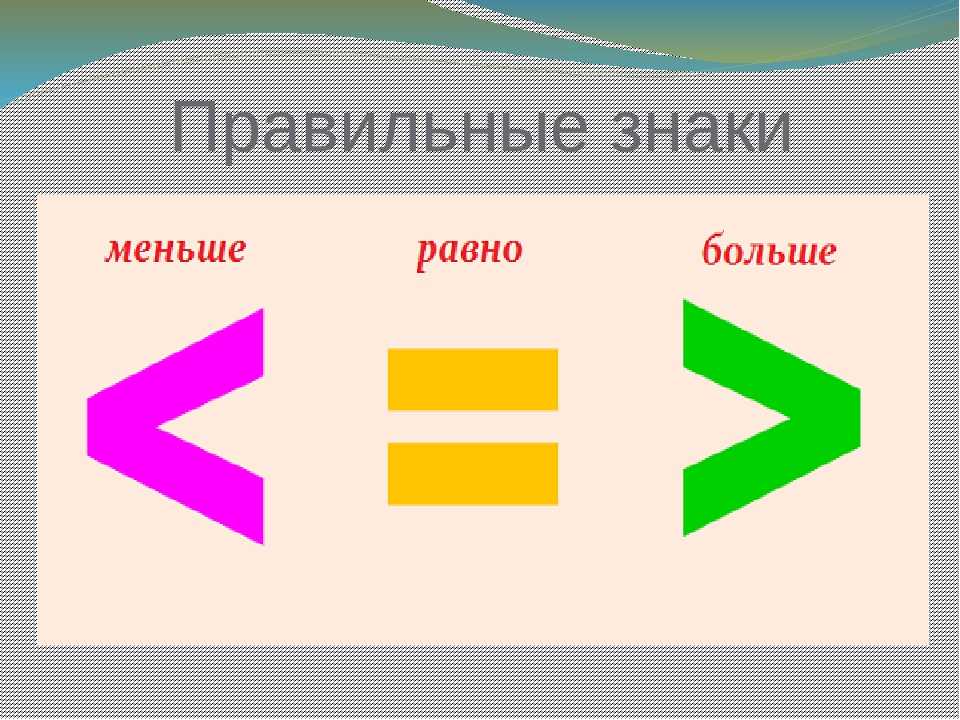 Значок @ применяется в коммерческих расчетах — в значении «по цене» (at the rate). Скажем, 10 галлонов масла по цене в 3,95 доллара США за галлон будет кратко записываться: 10 gal of oil @ $3.95/gal. В англоязычных странах символ применяется и в науке в значении «при»: например, плотность 1,050 г/см при 15°C будет записана: 1.050 g/cm @ 15°C. Кроме того, знак @ полюбили и часто используют анархисты ввиду его сходства с их символом — «А в круге». Однако его изначальное происхождение окутано тайной. С точки зрения лингвиста Ульмана, символ @ был изобретен средневековыми монахами для сокращения латинского ad («на», «в», «в отношении» и так далее), что очень напоминает его нынешнее использование. Другое объяснение дает итальянский ученый Джорджо Стабиле — он обнаружил этот символ в записях флорентийского купца Франческо Лапи за 1536 год в значении «амфора»: например, цена одной @ вина. Интересно, что испанцы и португальцы называют символ в электронных письмах именно «амфорой» (arroba) — словом, которое французы, исказив, превратили в arobase.
Значок @ применяется в коммерческих расчетах — в значении «по цене» (at the rate). Скажем, 10 галлонов масла по цене в 3,95 доллара США за галлон будет кратко записываться: 10 gal of oil @ $3.95/gal. В англоязычных странах символ применяется и в науке в значении «при»: например, плотность 1,050 г/см при 15°C будет записана: 1.050 g/cm @ 15°C. Кроме того, знак @ полюбили и часто используют анархисты ввиду его сходства с их символом — «А в круге». Однако его изначальное происхождение окутано тайной. С точки зрения лингвиста Ульмана, символ @ был изобретен средневековыми монахами для сокращения латинского ad («на», «в», «в отношении» и так далее), что очень напоминает его нынешнее использование. Другое объяснение дает итальянский ученый Джорджо Стабиле — он обнаружил этот символ в записях флорентийского купца Франческо Лапи за 1536 год в значении «амфора»: например, цена одной @ вина. Интересно, что испанцы и португальцы называют символ в электронных письмах именно «амфорой» (arroba) — словом, которое французы, исказив, превратили в arobase.![]() Впрочем, в разных странах существуют самые разные названия для символа @, чаще всего зоологические. Поляки называют его «обезьянкой», тайваньцы — «мышкой», греки — «уточкой», итальянцы и корейцы — «улиткой», венгры — «червячком», шведы и датчане — «слоновым хоботом», финны — «кошачьим хвостом» или «знаком мяу», а армяне, подобно нам, — «песиком». Есть гастрономические названия — «штрудель» в Израиле и «рольмопс» (сельдь под маринадом) в Чехии и Словакии. Кроме того, часто этот символ называют просто «скрюченным А», или «А с завитком», или, как сербы, «чокнутым А». Впрочем, самая удивительная из современных историй, связанных с символом @, произошла в Китае, где знак банально называется «А в круге». Несколько лет назад китайская пара дала такое имя новорожденному. Возможно, знак стали воспринимать как иероглиф, символизирующий технический прогресс, и решили, что он принесет счастье и успех юному обитателю Срединной державы.
Впрочем, в разных странах существуют самые разные названия для символа @, чаще всего зоологические. Поляки называют его «обезьянкой», тайваньцы — «мышкой», греки — «уточкой», итальянцы и корейцы — «улиткой», венгры — «червячком», шведы и датчане — «слоновым хоботом», финны — «кошачьим хвостом» или «знаком мяу», а армяне, подобно нам, — «песиком». Есть гастрономические названия — «штрудель» в Израиле и «рольмопс» (сельдь под маринадом) в Чехии и Словакии. Кроме того, часто этот символ называют просто «скрюченным А», или «А с завитком», или, как сербы, «чокнутым А». Впрочем, самая удивительная из современных историй, связанных с символом @, произошла в Китае, где знак банально называется «А в круге». Несколько лет назад китайская пара дала такое имя новорожденному. Возможно, знак стали воспринимать как иероглиф, символизирующий технический прогресс, и решили, что он принесет счастье и успех юному обитателю Срединной державы.
Символ математики Математические обозначения, Прод, угол, текст, прямоугольник png
Символ математики Математические обозначения, Прод, угол, текст, прямоугольник pngтеги
- угол,
- текст,
- прямоугольник,
- трава,
- число,
- структура,
- пи,
- таблица,
- символ,
- масштабируемая векторная графика,
- значки компьютеров,
- область,
- математическая задача,
- математическая запись,
- линия,
- зеленый,
- формула,
- уравнение,
- математика,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 900x900px
- Размер файла
- 21.
 15KB
15KB - MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
- математические уравнения, математические формулы, математические обозначения, cdr, угол, текст png 1080x763px 356.8KB
- Принципы и Стандарты для Школьной Математики Уравнение, Математика, текст, число, принципы и стандарты для школы Математика png 1000x1000px 228.64KB
- Формула Математика Евклидова, математическая формула, угол, текст, монохромный png 3500x3313px 875.77KB org/ImageObject»> Математика геометрия формула евклидово уравнение, математические заметки, угол, текст, треугольник png 6354x6354px 911.07KB
- Решение уравнений Математика Математическая запись Формула, администратор, текст, число, математик png 792x658px 240.21KB
- Математические уравнения, Формула Математика Функция Евклида, Оси математических функций, синий, угол, текст png 800x800px 366.32KB
- Плюс и минус + сложение математики, плюс, прямоугольник, плюс, крест png 600x598px 39.14KB
- Таблица умножения Математика Число, Математика, текст, прямоугольник, число png 700x525px 37.36KB org/ImageObject»> логотип с зеленым крестом, знаки плюс и минус + дополнение, знак плюс, прямоугольник, крест, знак png 768x768px 84.82KB
- Математика евклидова геометрия формула, математика, угол, текст, треугольник png 4050x4050px 420.75KB
- Математика, математика, евклидова формула Компьютерный файл, рукописная математическая формула, угол, текст, класс png 4520x3161px 338.87KB
- Математическая нотация Математический символ Номер, математические символы, угол, белый, текст png 1024x683px 56.5KB
- Математика Алгебра Бесплатный контент, Математика, текст, число, символ png 1024x1024px 912.26KB org/ImageObject»> Пи день символ математики, пи, разное, текст, логотип png 600x588px 15.69KB
- Математика евклидова формула бумаги, математические различные формулы, угол, текст, монохромный png 4050x4050px 627.53KB
- символ равенства, знак равенства символ равенства, знак равенства, разное, прямоугольник, черный png 543x768px 4.3KB
- Знак равенства Математика Компьютерные иконки, Большой знак равенства, угол, прямоугольник, знак png 512x512px 115KB
- Математика Математическая запись Компьютерные иконки Математик, Математика, угол, текст, логотип png 600x564px 12.32KB org/ImageObject»> Математическая формула Алгебра Евклидова, Математическая формула, угол, текст, монохромный png 2244x2244px 134.04KB
- Суммирование Математический символ Математическая запись Сигма, суммирование, угол, текст, треугольник png 512x512px 5.76KB
- круглый красный знак, без символа знак равенства компьютерные иконки, запрещенный знак, угол, текст, товарный знак png 600x600px 19.53KB
- Дополнение Математика Математическая запись, геоментрия, текст, знак, число png 1729x2107px 78.61KB
- зеленый туннель Super Mario art, Марио Пайп, Водопровод s-, угол, текст, прямоугольник png 705x900px 5.63KB org/ImageObject»> иллюстрация чисел и математических операций, евклидова икона, учебник математики, ребенок, малыш, с днем рождения векторные изображения png 1600x1600px 445.09KB
- Число математики в день Пи, математика пи, разное, текст, числовая цифра png 1600x1593px 791.84KB
- Математика Математическая запись Математическая задача Алгебра Геометрия, Математика, угол, текст, число png 1285x857px 129.68KB
- красная стрелка, Иконка Стрелка компьютера, Красная линия стрелки, разное, угол, текст png 600x529px 15.53KB
- уравнения и графики, евклидово математическое уравнение формулы, проблема плавающей математики неверна, плавающий, угол, текст png
4050x4050px
839.
 34KB
34KB - две зеленые параллельные линии иллюстрации, знак равенства компьютерные иконки Green Equality, Equal s, текст, прямоугольник, трава png 512x512px 5.19KB
- Математическое образование Презентация Уравнение Математическая запись, Математика, синий, текст, умножение png 1600x711px 949.64KB
- Математика уравнения анимации чисел алгебра, математика, текст, рука, степень png 1600x1200px 731KB
- черно-фиолетовая текстовая иллюстрация, Бумажная математическая формула науки, Фиолетовые математические заметки, угол, текст, симметрия png 4050x4050px 788.52KB org/ImageObject»> красный крест, сложение плюс и минус +, плюс, прямоугольник, компьютер, плюс png 600x598px 21.4KB
- Длинное деление Математика Математическая запись Символ Квадратный корень, Математика, угол, текст, прямоугольник png 1000x1000px 10.76KB
- Математика Уравнение Угол Почерк, рукописная математическая формула, белый, текст, прямоугольник png 900x1111px 11.38KB
- нажмите значок руки, значок указателя компьютера и нажмите курсор, значок руки нажмите, cdr, текст, компьютер png 822x981px 49.51KB
- Круг окружности символа Пи Пи, пи, разное, угол, текст png 2000x1935px 38.72KB org/ImageObject»> математическая формула, математическая формула, евклидово суммирование, фиг., синий, угол, текст png 800x793px 185.06KB
- значок со стрелкой вправо, значки со стрелками компьютера, файл с синей стрелкой, разное, синий, угол png 512x512px 6.51KB
- Знак умножения математики Таблица умножения, кейри, несколько, знак, число png 600x599px 101.38KB
- Символ Математика Математическая запись, математические символы, Разное, текст, с днем рождения Векторные изображения png 1184x594px 52KB
- Математическая иллюстрация, математическое евклидово число, дети, интересующиеся математикой, ребенок, текст, дети png
813x926px
215.
 21KB
21KB - Пи день математики, пи, Разное, текст, логотип png 882x854px 17.14KB
- Пи Дэй Символ Математика, математика, разное, текст, логотип png 800x709px 11.87KB
- серая и синяя спиральная графика, математическая евклидова формула, креативная тяга синего пространства бесплатно, синий, угол, свободный Шаблон дизайна логотипа png 5314x3543px 12.85MB
- Зеленая стрела, стрела, угол, текст, прямоугольник png 1773x1581px 124.62KB
- Математика Математическая запись Наука, Математика Графика, текст, измерение, логотип png 600x600px 104.08KB org/ImageObject»> красная мишень, телескопический прицел, перекрестие с, угол, текст, симметрия png 1024x1024px 88.98KB
- Знак равенства Символ равенства Математическая запись, геометрия моды, разное, угол, логотип png 800x800px 10.35KB
- уравнение, математика рисования евклидова, математические задачи, угол, карандаш, текст png 5111x3571px 218.17KB
Математические знаки и символы — Карточки и Задания для детей
Большое значение в математике имеют математические знаки и символы, благодаря которым выполняются различные действия: сложения, вычитания, деления, умножения, равенства и сравнения. Для детей достаточно и этих знаков, хотя в математике их гораздо больше. Но так как мы разрабатываем материалы для детей, то ограничимся самыми основными знаками и действиями математической науки.
Здесь вы найдете массу полезных математических заданий на сравнение чисел, а также счет до 10, примеры в картинках, раскраски и множество других развивающих заданий для детей, которые учатся в 1 классе, и для тех, которые только готовятся к поступлению в школу.
Очень удобно проводить учебные занятия по математике с детьми, используя математические знаки и символы в виде карточек. Их нужно распечатать, вырезать и использовать для составления примеров или заданий.
С распечатанным материалом можно придумывать самостоятельно различные задания. Например, положить на стол цветные карандаши, затем разделить их на две части. Попросить ребенка, чтобы он посчитал и сказал, в какой части карандашей больше (или меньше). Пусть положит между ними соответствующий математический знак. То же самое задание можно выполнять и с цифрами.
Но если ребенку с цифрами работается еще трудно, то лучше разнообразьте задания различными предметами. Пусть сравнивает количество маленьких и больших монет, ложек, конфет и любых других мелких предметов. Передайте инициативу по выбору предметов ребенку. Попробуйте с ним составить пример с помощью предметов. Попросите ребенка самого составить любой пример, используя различные предметы и вырезанные математические знаки.
Передайте инициативу по выбору предметов ребенку. Попробуйте с ним составить пример с помощью предметов. Попросите ребенка самого составить любой пример, используя различные предметы и вырезанные математические знаки.
Скачать математические знаки и символы в виде карточек для вырезания вы можете во вложениях.
Посчитай и поставь подходящие математические знаки
В этих новогодних картинках от ребенка требуется правильно расставить математические знаки, а также закончить примеры. Для этого необходимо сначала посчитать количество предметов с левой стороны в обоих квадратах и вписать количество предметов в одном квадрате, во втором квадрате и их сумму в пустые клетки для примера под квадратами. То же самое нужно проделать и с левой стороны. После сравнения обеих сторон — поставить между ними подходящий знак.
Скачать учебный бланк с математическими знаками вы можете во вложениях.
Поставь нужный знак — Больше, меньше, знак равенства, плюс или минус
Здесь вы можете скачать еще одно упражнение, в котором нужно правильно составить и дорешать примеры с математическими знаками.![]() Чтобы выполнить задания, ребенок должен свободно владеть счетом от 1 до 10. Опять же, для привлечения внимания ребенка задания представлены в красочном оформлении.
Чтобы выполнить задания, ребенок должен свободно владеть счетом от 1 до 10. Опять же, для привлечения внимания ребенка задания представлены в красочном оформлении.
- В первом задании нужно посчитать предметы в каждом прямоугольнике и вписать соответствующее число под ним. Между числами нужно поставить нужный математический знак, сравнивая эти числа между собой — одно число больше другого, меньше или они равны.
- Во втором задании даны примеры, в которых складываются и вычитаются различные геометрические фигуры. Вот только в этих примерах отсутствуют математические знаки «+» и «-«. Ребенок должен написать эти знаки вместо звездочек, чтобы ответ примера получился верным.
Скачать задания — Поставь нужный знак — вы можете во вложениях внизу страницы
Задания для детей — Раскрась, найди соседей, подбери знаки, составь примеры
В этом упражнении несколько интересных заданий, для выполнения которых детям понадобятся не только знания математических знаков, но и умение считать, составлять примеры, а также находить соседей чисел (руководствуясь порядковым счетом от 0 до 10).![]()
- В первом задании нарисованы медведи. Ребенку нужно раскрасить такое количество медведей (можно в разные цвета), которое соответствует числу 10. Вопрос ребенку нужно задавать именно так, как написано на картинке.
- Во втором задании каждая строчка — это порядковый ряд чисел от 0 до 10 или от 10 до 0. Ребенку нужно по вписанным числам определить, какой порядок чисел у каждой строки (на увеличение или на уменьшение), а затем вписать в пустые клетки недостающие числа. В последней строке совсем отсутствуют числа, поэтому ребенку нужно будет ориентироваться по начальной клетке (она состоит из двух квадратиков, значит в ней написано двузначное число, т.е. 10). Но не подсказывайте ребенку — он должен додуматься до этого самостоятельно!
- В третьем задании нужно сравнить указанные числа между собой и поставить нужный математический знак или символ.
- В четвертом задании нужно решить примеры в картинках, отнимая или прибавляя предметы. Ответы нужно вписывать не числами, а овалами (какое число, столько овалов и нужно вписать в клетки.
 В каждой клетке — 1 овал). Затем можно попросить ребенка записать в числовом виде все примеры (можно на отдельном листе).
В каждой клетке — 1 овал). Затем можно попросить ребенка записать в числовом виде все примеры (можно на отдельном листе).
Скачать 4 задания с раскрасками, счетом и примерами вы можете во вложениях.
Задания на математическое сравнение количества предметов
Тренируемся дальше в освоении математического сравнения, используя основные математические знаки «>» — больше, «» — меньше и «=» — знак равенства. Скачайте и распечатайте картинку с заданиями, подготовьте простой карандаш, ластик и, при желании, цветные карандаши.
- В первом задании даны уже готовые примеры на сравнение. Но количество нарисованных геометрических фигур не соответствует знаку между ними — каких-то предметов не хватает. Ребенку нужно дорисовать недостающее количество справа или слева, чтобы знак оказался верным.
- Во втором задании нужно не дорисовать предметы (как в первом задании), а зачеркнуть лишние. Так как здесь математические знаки тоже проставлены неверно.

Скачать учебный бланк с фигурами и предметами для сравнения вы можете во вложениях.
Веселые задания на сравнение с героями мультфильмов
В этих веселых задания для детей вы можете проверить не только умение ребенка ставить математические знаки между числами, но и его память — ведь ему придется вспомнить имена всех героев мультфильмов и сказок, нарисованных ка картинке.
- В первом задании ребенок сначала должен сказать название двух сказок, героев которых он видит на картинке. Слева — одна сказка, а справа — другая. Затем ему нужно хорошо подумать и вспомнить, какие еще герои были в этих сказках — кого забыли нарисовать художники? Пусть ребенок дорисует недостающих персонажей. После этого ему нужно пересчитать отдельно персонажей одной сказки и другой, поставив между ними соответствующий математический знак.
- Во втором задании ребенку нужно назвать всех персонажей известных мультфильмов, пересчитать их с левой и с правой стороны, а затем поставить необходимый математический знак между ними.
 Некоторые персонажи встречаются на картинке несколько раз. Пусть ребенок назовет их и посчитает, сколько раз каждый из них повторяется.
Некоторые персонажи встречаются на картинке несколько раз. Пусть ребенок назовет их и посчитает, сколько раз каждый из них повторяется.
Скачать учебный бланк с героями мультфильмов вы можете во вложениях.
Задачи для детей на сравнение — Больше и меньше
В этих красочных заданиях с примерами на сравнение для детей встречается и счет до 10, и четные и нечетные числа, и математические знаки, и вопрос на развитие логического мышления. Скачайте и распечатайте картинку во вложениях и прочитайте ребенку условия заданий.
- В первом задании ребенок должен пересчитать все предметы в прямоугольниках, а затем обвести карандашом соответствующее слово над картинками. После этого нужно сравнить количество предметов справа и слева, подумать, где предметов больше (или меньше), и поставить между прямоугольниками нужный математический знак.
- Во втором задании также необходимо пересчитать в обоих прямоугольниках всех мультяшных зверей и обвести карандашом соответствующее число.
 Затем ребенок должен ответить на вопрос, в каком прямоугольнике четное число зверей, а в каком нечетное? Поставить между двумя прямоугольниками правильный математический знак.
Затем ребенок должен ответить на вопрос, в каком прямоугольнике четное число зверей, а в каком нечетное? Поставить между двумя прямоугольниками правильный математический знак. - В третьем задании нарисованы сладости — мороженые и пирожные. Все сладости ждут своих гостей, которые должны прийти к девочке на день рождения. Известно, что для каждого гостя заготовлены 1 мороженое и 1 пирожное. Задача ребенка — подумать и сказать, сколько гостей придет?
Скачать красочные задания с математическими знаками вы можете во вложениях.
Составь примеры с математическими знаками по картинкам
Очень полезно для дошкольников, как и для учеников младших классов, умение составлять примеры с математическими знаками по картинкам. С помощью данных заданий дети потренируются в этом нелегком деле, заодно повторяя счет до 10.
- В первом задании нужно составить пример с математическим знаком, который покажет кого больше (или меньше) — бабочек или пчелок.

- Во втором задании ребенок должен посчитать и сказать, на сколько больше лягушек, чем божьих коровок. Затем пусть ребенок подумает и ответит: что нужно сделать, чтобы их стало поровну (убрать одну лягушку)? После этого нужно подумать, сколько станет божьих коровок, если прилетит еще одна? — Записать это в виде примера.
- В третьем задании нужно посчитать, сколько останется божьих коровок, если несколько из них перелетели на ветку. — Записать это в виде примера.
Скачать примеры с математическими знаками по картинкам вы можете во вложениях.
Изучаем математические знаки — плюс, минус и знак равенства
С помощью следующих заданий можно научить дошкольника писать математические знаки — плюс, минус и знак равенства, а также познакомят его с простыми примерами в картинках на сложение и вычитание. Выполнять такие задания можно уже с 4-5 лет.
Задание №1
Посмотри на самый добрый знак — плюс, который похож на крестик. Почему он добрый? — Потому что всегда что-то прибавляет.![]() Посмотри на картинке, как плюс прибавил к двум яблокам еще одно, а к двум конфетам — еще две. Обведи математические знаки в больших квадратах.
Посмотри на картинке, как плюс прибавил к двум яблокам еще одно, а к двум конфетам — еще две. Обведи математические знаки в больших квадратах.
Задание №2
А теперь познакомься со знаком минус. Минус — очень жадный. Он всегда у всех что-то отнимает. Внимательно посмотри на картинку и ты увидишь, как он отнял от торта целых три кусочка! А от двух воздушных шариков отнял один шарик. Обведи минус в больших квадратах под картинками.
Задание №3
А теперь ты увидишь знак равенства — он самый дружественный. Потому что уравнивает все предметы и числа, так, что никто ни на кого не в обиде. Справа и слева от этого знака всегда находится одинаковое количество предметов. Обведи по точкам знак равенства в квадратах.
Также вам пригодятся и другие материалы для распечатки, в которых встречаются математические знаки:
Примеры по математике — 1 класс — Распечатать в картинках
Здесь вы можете найти примеры по математике (1 класс), распечатать на принтере и использовать в качестве учебного материала на уроках математики или в детских садах.
Учимся считать до 20 с героями мультфильмов
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Устный счет в пределах 10 — Картинки с заданиями
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
А еще вы можете встретить математические знаки в математических играх от лисенка Бибуши:
Игра «Сложение и вычитание до 10» — Задачки в картинках
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши, в которой малыш сможет решить восемь новых задачек на счет до 10.
Задачи-примеры для малышей в картинках
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10. В трех уровнях игры ребенок будет решать задачи на вычитание, а в пяти — складывать заданные предметы.
Вставка математических знаков
Word для Microsoft 365 Word 2021 Word 2019 Word 2016 Word 2013 Word 2010 Word 2007 Еще…Меньше
В Word можно вставлять математические символы в уравнения и текст.
-
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
org/ListItem»>
-
Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.
-
Щелкните нужный символ.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
|
Набор символов |
Подгруппа |
Определение |
|---|---|---|
|
Основные математические символы |
Нет |
Часто используемые математические символы, такие как > и < |
|
Греческие буквы |
Строчные буквы |
Строчные буквы греческого алфавита |
|
Прописные буквы |
Прописные буквы греческого алфавита |
|
|
Буквоподобные символы |
Нет |
Символы, которые напоминают буквы |
|
Операторы |
Обычные бинарные операторы |
Символы, обозначающие действия над двумя числами, например + и ÷ |
|
Обычные реляционные операторы |
Символы, обозначающие отношение между двумя выражениями, такие как = и ~ |
|
|
Основные N-арные операторы |
Операторы, осуществляющие действия над несколькими переменными |
|
|
Сложные бинарные операторы |
Дополнительные символы, обозначающие действия над двумя числами |
|
|
Сложные реляционные операторы |
Дополнительные символы, обозначающие отношение между двумя выражениями |
|
|
Стрелки |
Нет |
Символы, указывающие направление |
|
Отношения с отрицанием |
Нет |
Символы, обозначающие отрицание отношения |
|
Наборы знаков |
Наборы знаков |
Математический шрифт Script |
|
Готические |
Математический шрифт Fraktur |
|
|
В два прохода |
Математический шрифт с двойным зачеркиванием |
|
|
Геометрия |
Нет |
Часто используемые геометрические символы |
Дополнительные сведения
Вставка флажка или другого символа
2 \ge 0 ] \end{gather*} \] Математический символ может использоваться для различных целей из одного математического подполя в другое (например, $\sim$ как логическое отрицание и подобие треугольника), так же как и несколько символов может использоваться для обозначения одного и того же понятия или отношения (например, $\times$ и $\cdot$ при умножении).
Базовое понимание математической терминологии необходимо для прочного фундамента в высшей математике. С этой целью ниже приводится подборка некоторых из наиболее хорошо адаптированных общеупотребительные символы в математике.
Кроме того, эти символы далее классифицируются по их функции в таблицы. Более полные списки символов, классифицированные по тематике , и , типу , также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите полный исчерпывающий список математических символов в электронной книге , форма — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Константы
В математике константы — это символы, которые используются для обозначения неизменяющихся объектов . Это могут быть ключевые числа, ключевые математические наборы, ключевые математические бесконечности и другие ключевые математические объекты (например, единичная матрица $I$).![]()
Математические константы часто принимают форму буквы алфавита или производной от нее. В некоторых случаях константа может рассматриваться как переменная в более широком контексте. В следующих таблицах представлены некоторые наиболее часто используемые константы, а также их имена, значения и использование.
Key Mathematical Numbers
| Symbol Name | Explanation | Example |
|---|---|---|
| $0$ ( Zero ) | Additive identity of common numbers | $3 + 0 =3$ |
| $1$ ( One ) | Мультипликативное тождество обычных чисел | $5 \times 1 = 5$ |
| $\sqrt{2}$ ( Квадратный корень из $2$ ) | 9005 Положительное число, квадрат которого равен 5 $2$. Приблизительно $1.41421$. 92 = 2i$
Основные математические наборы
Более полный список см. в разделе ключевых математических наборов по алгебре .
в разделе ключевых математических наборов по алгебре .
| Название символа | Объяснение | Пример |
|---|---|---|
| $ \ varnothing $ ( пустой набор ) | SET с NOE Element | $ | varnothing | varnothing | varnothing | varnothing | varnothing | varnothing | varnothing | varnothing | varnothing | varnothing | = 0$ |
| $\mathbb{N}$ ( N ) | Набор натуральных чисел | $\forall x, y \in \mathbb{N}$, $x+y \in \mathbb{N}$ |
| $\mathbb{Z}$ ( Z ) | Набор целых чисел (Z означает zahlen, номер на немецком языке) | $ \mathbb{N} \subseteq \mathbb{Z}$ |
| $\mathbb{Z}_+$ ( Z-plus ) | Набор натуральные числа | $3 \in \mathbb{Z}_+$ |
| $\mathbb{Q}$ ( Q ) | Набор рациональных чисел (Q означает частное) | 93$
Ключевые математические бесконечности
В математике существует множество различных типов бесконечности .![]() К ним относятся чисто условное использование символа лемнискаты ($\infty$) и использование следующих символов в контексте количественных/порядковых бесконечностей:
К ним относятся чисто условное использование символа лемнискаты ($\infty$) и использование следующих символов в контексте количественных/порядковых бесконечностей:
| Название символа | Объяснение | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $\aleph_0$ ( Алеф-ноль ) | Мощность множества натуральных чисел 9{\aleph_0}$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\omega$ ( Omega ) | Наименьшее бесконечное порядковое число | $\forall n \in \mathbb{N}, n < \omega$ |
| Название символа | Объяснение | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $ \ Mathbf {0} $ ( Zero | 9 $ \ \0055 Нулевой вектор векторного пространства $\forall \mathbb{v} \in V$, $\mathbf{v} + \mathbf{0} = \mathbf{v}$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $e$ ( E ) | Identity element of a group | $e \circ e = e$ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $I$ ( I ) | Identity matrix | $AI = IA =I$ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $C$ ( C ) | Константа интегрирования | $\displaystyle \int 1 \, \mathrm{d}x =$ $x + C$ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\top$ ( Тавтология ) | Предложение в формальной логике, безусловно истинное | Для каждого предложения $P$, $P \land \top \equiv P$. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\bot$ ( Противоречие ) | Предложение формальной логики, безусловно ложное | Для каждого предложения $P$, $P \land \lnot P \equiv \bot.$ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стандартное нормальное распределение | $Z \sim N(0,1)$ 9x = y) \end{gather*} В некоторых случаях переменные можно рассматривать как константы в более узком контексте (например, как параметры), в то время как в других случаях переменные используются в сочетании с индексами для составления из-за отсутствия букв (например, $x_3$). Хотя переменные в математике часто используются для представления чисел , они также могут использоваться для представления других объектов, таких как векторы, функции и матрицы. В следующих таблицах описаны некоторые из наиболее распространенных соглашений для переменных, а также контекст, в котором они приняты и используются. Переменные для номеров
Переменные в геометрииДополнительные символы в геометрии и тригонометрии см. в разделе символы геометрии и тригонометрии .
Переменные в исчисленииБолее полный список см. в разделе константы и переменные в исчислении .
Переменные в линейной алгебре 9 , см.переменных в алгебре .
Переменные в теории множеств и логике Более подробные списки тем см.
Переменные вероятности и статистикиБолее полный список вероятностей см. в 90 и статистика .
Разделители Подобно знакам препинания в английском языке, разделители представляют собой набор символов, обозначающих границы между независимыми математическими выражениями. Они часто используются для указания области применения операции или правила и могут встречаться как в виде изолированного символа, так и в виде пары противоположно выглядящих символов. Во многих сценариях разделители используются главным образом для целей группировки . В следующей таблице представлены некоторые из наиболее часто используемых разделителей, а также их функции и использование.
ОператорыОператор — это символ, используемый для обозначения операции — функции, которая переводит один или несколько объектов в другой подобный объект. Большинство операторов являются унарными и бинарными по своей природе (т. е. передают один и два входа к намеченной цели соответственно), причем наиболее распространенными из них являются арифметические операторы (например, $+$). Как и в случае с английским языком, операторы позволяют расширить словарный запас математики, где существует только конечное число символов. В следующих таблицах представлены некоторые из наиболее часто используемых операторов в математике, а также их использование и предполагаемое значение. Обычные операторы
Операторы, связанные с функциями Более полный список см.
список см.
Геометрические операторыДополнительные символы в геометрии и тригонометрии см. в разделе символы геометрии и тригонометрии .
Логические операторыБолее подробно список см. операторы в логике .
Векторные операторыБолее полный список см. в разделе операторов линейной алгебры .
Матричные операторы Более полный список см.
Вероятностные операторыБолее полный список см. в разделе операторов вероятности и статистики .
Ключевые функции вероятности и распределенияБолее полный список см. в разделе операторы, связанные с распределением вероятностей .
Операторы, связанные с вычислениямиБолее полный список см. в разделе символы исчисления и анализа .
Символы отношенийСимволы отношений используются для выражения математических отношений между несколькими объектами. Многие относительные символы являются бинарными по своей природе, поскольку они принимают два объекта в качестве входных данных и превращают их в полные осмысленные предложения (как в случае символа неравенства $<$). Поскольку реляционные символы образуют строительные блоки математических предложений , они имеют фундаментальное значение в математике. В следующих таблицах описаны некоторые из наиболее часто используемых реляционных символов, а также их использование и значение. Основанные на равенстве реляционные символы
Реляционные символы, основанные на сравненииДля более полного списка см.
Number-related Relational Symbols
Geometry-related Relational Symbols Дополнительные символы в геометрии и тригонометрии см.
Реляционные символы, связанные с логикойБолее полный список см. в разделе реляционные символы в логике .
Реляционные символы, связанные с вероятностьюБолее полный список см. в разделе реляционных символов в теории вероятностей и статистике .
Реляционные символы, связанные с вычислениямиБолее полный список см. в разделе реляционных символов в асимптотическом анализе .
Символы нотации Символ нотации — это соглашение или сокращение , роль которого отличается от роли константы, переменной, разделителя, оператора или реляционного символа. Общие обозначения
Обозначения в геометрии и тригонометрииДополнительные символы в геометрии и тригонометрии см. 9{\ Circ} $ ∟ | ПРАВИЛЬНЫЙ УГОЛ | $-$, $ = $ $ \ Equiv $ | ООЛ | Обозначения в исчисленииДополнительные символы в исчислении см. в разделе символы исчисления и анализа .
Обозначения в вероятности и Статистика Более полный список см.
Списки символов, классифицированных по типам и по теме , см. на соответствующих страницах ниже. Предпочитаете версию в формате PDF? Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX. Да. Это было бы полезно. Дополнительные ресурсы
Общие математические символы и терминология Математические символы и терминология могут сбивать с толку и мешать обучению и пониманию основ счета. Эта страница дополняет наши страницы навыков счета и содержит краткий глоссарий общих математических символов и терминологии с краткими определениями. Мы что-то упустили? Свяжитесь с нами, чтобы сообщить нам об этом. Общие математические символы+ Сложение, плюс, положительныйСимвол сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2. Символ + также может использоваться для обозначения положительного числа, хотя это менее распространено, например, +2. На нашей странице положительных и отрицательных чисел объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется. Дополнительную информацию см. на нашей странице Дополнение . − Вычитание, минус, отрицательныйЭтот символ имеет два основных применения в математике:
Подробнее см. на нашей странице Вычитание . × или * или . УмножениеЭти символы имеют одинаковое значение; обычно × используется для обозначения умножения, когда пишется от руки или используется на калькуляторе, например, 2 × 2. Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет и другие, более сложные значения в математике. Реже умножение может обозначаться точкой . или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2(3+2) равно 2×(3+2). См. нашу страницу Умножение для большего. ÷ или / Деление Оба эти символа используются для обозначения деления в математике. / используется в электронных таблицах и других компьютерных приложениях. Дополнительную информацию см. на нашей странице Division . = равноСимвол = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего он используется для отображения результата вычисления, например, 2 + 2 = 4, или в уравнениях, таких как 2 + 3 = 10 — 5,9.0004 Вы также можете встретить другие связанные символы, хотя они менее распространены:
< Меньше и > Больше Этот символ < означает меньше, например, 2 < 4 означает, что 2 меньше 4. Этот символ > означает больше, чем, например, 4 > 2 ≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и >=. ≪ ≫ Эти символы менее распространены и означают намного меньше или намного больше. ± Плюс или минусЭтот символ ± означает «плюс или минус». Он используется для указания, например, доверительных интервалов вокруг числа. Говорят, что ответ представляет собой «плюс-минус» другое число, или, другими словами, находится в диапазоне от заданного ответа. Например, 5 ± 2 на практике может быть любым числом от 3 до 7. ∑ СуммаСимвол ∑ означает сумму. ∑ — греческая заглавная сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — значок кнопки «Автосумма» имеет сигму в качестве значка. ° ГрадусыГрадусы ° используются по-разному.
∠ Угол Символ угла ∠ используется в качестве сокращения в геометрии (науке о формах) для описания угла. Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC будет использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. на наших страницах Геометрия . √ Квадратный корень√ — это символ квадратного корня. Квадратный корень — это число, которое при умножении само на себя дает исходное число. Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9равно 3, потому что 3 x 3 = 9. См. нашу страницу: Специальные числа и концепции , чтобы узнать больше о квадратных корнях. n Степень Целое число с надстрочным индексом (любое целое число n ) — это символ степени числа. Например, 3 2 означает 3 в степени 2, что равно 3 в квадрате (3 x 3). 4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4. См. наши страницы Вычисление площади и Вычисление объема для примеров использования чисел в квадрате и кубе . Полномочия также используются для записи больших и малых чисел. Большие числа 10 6 равны 1 000 000 (один миллион). 10 9 составляет 1 000 000 000 (один миллиард). 10 12 равно 1 000 000 000 000 (один триллион). 10 96 = 10 6 = 1 000 000 (один миллион). . Десятичная точка. — это десятичный символ точки, часто называемый просто «точкой». См. нашу страницу Decimals для примеров его использования. , Разделитель тысячЗапятая может использоваться для разделения больших чисел и облегчения их чтения. Тысяча может быть записана как 1000, а также 1000, а миллион как 1000000 или 1000000. В большинстве англоязычных стран символ , не имеет никакой математической функции, он просто используется для облегчения чтения чисел. В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers . [ ], ( ) Скобки, круглые скобкиСкобки ( ) используются для определения порядка вычислений в соответствии с правилом BODMAS. Части расчета, заключенные в скобки, вычисляются первыми, например,
% PercentageThe % symbol means percentage, or the number out of 100. Learn all about percentages on our page: Introduction to Percentages π Pi π or Pi is греческий иероглиф для звука «п». ∞ БесконечностьСимвол ∞ означает бесконечность, понятие, что числа продолжаются вечно. Каким бы большим ни было ваше число, вы всегда можете получить большее число, потому что вы всегда можете добавить к нему единицу. Бесконечность — это не число, а идея чисел, продолжающихся вечно. Вы не можете добавить единицу к бесконечности, так же как вы не можете добавить единицу к человеку, любить или ненавидеть. \(\bar x\) (x-bar) Среднее\(\bar x\) является средним значением всех возможных значений x. Этот символ чаще всего встречается в статистике. Дополнительную информацию см. на нашей странице Averages . ! Факториал! является символом факториала. н! есть произведение (умножение) всех чисел от n до 1 включительно, т. е. n × (n−1) × (n−2) × … × 2 × 1, Например: 5! = 5 × 4 × 3 × 2 × 1 = 120 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3 628 800 | ТрубаТруба ‘|’ также упоминается как вертикальная полоса, vbar, пика и имеет множество применений в математике, физике и вычислительной технике. Чаще всего в базовой математике используется для обозначения абсолютного значения или модуля действительного числа, где \(\vert x \vert\) – абсолютное значение или модуль \(x\) . Математически это определяется как $$\vert x \vert = \biggl\{\begin{eqnarray} -x, x \lt 0 \\ x, x \ge 0 \end{eqnarray}$$ Проще говоря, \(\vert x \vert\) является неотрицательным значением \(x\). Например, модуль 6 равен 6, а модуль -6 также равен 6. Он также используется в вероятности, где P(Z|Y) обозначает вероятность X при заданном Y. ∝ Пропорциональный∝ означает «пропорционально » и используется, чтобы показать что-то, что изменяется по отношению к чему-то другому. Например, если x = 2y, то x ∝ y. ∴ Поэтому∴ — полезная сокращенная форма «следовательно», используемая в математике и естественных науках. ∵ Потому что∵ — полезная сокращенная форма «потому что», не путать с «поэтому». Математическая терминология (A-Z)Амплитуда Когда объект или точка движется циклически или подвергается вибрации или колебаниям (например, маятник), 9Амплитуда 3111 — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. введение в геометрию для получения дополнительной информации. Апофема Линия, соединяющая центр правильного многоугольника с одной из его сторон. Площадь Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например, в квадратных метрах (м 2 ). Для получения дополнительной информации см. нашу страницу на площадь, площадь поверхности и объем . Асимптота Асимптота — это прямая линия или ось, которая конкретно связана с кривой линией. По мере того, как кривая линия простирается (стремится) к бесконечности, она приближается к своей асимптоте, но никогда не касается ее (то есть расстояние между кривой и асимптотой стремится к нулю). Встречается в геометрии и тригонометрии . Ось Линия отсчета, вокруг которой рисуется, вращается или измеряется объект, точка или линия. В симметричной форме ось обычно представляет собой линию симметрии. Коэффициент Коэффициент — это число или величина, умноженная на другую величину. Окружность Окружность — это длина расстояния вокруг края круга. Это тип периметра , уникальный для круглых форм. Подробнее см. на нашей странице изогнутых форм . Данные Данные представляют собой совокупность значений, информации или характеристик, которые часто имеют числовую природу. Их можно собрать с помощью научных экспериментов или других средств наблюдения. Они могут быть количественными или качественными переменными. Данные — это единичное значение одной переменной. Подробнее см. на нашей странице Типы данных . Диаметр Диаметр — термин, используемый в геометрии для обозначения прямой линии, проходящей через центр круга или сферы и касающейся окружности или поверхности на обоих концах. Диаметр в два раза больше радиус . Экстраполировать Экстраполировать — это термин, используемый при анализе данных. Фактор Фактор — это число, которое мы умножаем на другое число. Множитель делится на другое число целое число раз. Большинство чисел имеют четное число множителей. Число в квадрате имеет нечетное количество делителей. А 9Простое число 3111 имеет два делителя — само себя и 1. Простой делитель — это делитель, который является простым числом. Например, простые делители числа 21 — это 3 и 7 (поскольку 3 × 7 = 21, а 3 и 7 — простые числа). Среднее, медиана и мода среднее (среднее) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе. Когда набор данных упорядочен от наименьшего к наибольшему, медиана является средним значением. Мода — это число, которое встречается чаще всего. Операция Математическая операция — это шаг или этап вычисления или математическое «действие». К основным арифметическим действиям относятся сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при расчете, важен. Порядок операций известен как BODMAS . Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы говорим об операциях и вычислениях, но в повседневном языке часто можно услышать неверный общий термин «суммы». Периметр Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы специально называется ее окружностью . Наша страница Периметр объясняет это более подробно. Пропорция Пропорция является относительным отношением. Отношения сравнивают одну часть с другой частью, а пропорции сравнивают одну часть с целым. Например, «3 из каждых 10 взрослых в Англии имеют избыточный вес». Пифагор Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, самое значительное из которых стало известно как Теорема Пифагора . Это важное правило применимо только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов двух других сторон». Количественный и качественный Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, т. е. сколько, сколько, как часто, и получены путем подсчета или измерения. Качественные данные представляют собой переменные типа, которые не имеют числового значения и могут быть выражены описательно, т. е. с использованием имени или символа, и получены путем наблюдения. Подробнее см. на нашей странице типов данных . Радиан Радиан — это единица измерения углов в системе СИ. Радиус Термин радиус используется в контексте кругов и других изогнутых форм. Это расстояние от центральной точки круга, сферы или дуги до их внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Подробнее см. на нашей странице изогнутых форм . Диапазон В статистике диапазон данного набора данных представляет собой разницу между наибольшим и наименьшим значениями. Коэффициент Соотношение — это математический термин, используемый для сравнения размера одной части с другой частью. Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7:5, 1:8 или 5:2:1. Стандартное отклонение Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, т. Термин Термин — это отдельное математическое выражение. Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, перемноженных вместе (например, 3 x 2). Члены обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например. 3(2-x3). Переменная Переменная фактор в математическом выражении, арифметическом соотношении или научном эксперименте, который может быть изменен. Эксперимент обычно имеет три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , и x — это переменная. Дисперсия Дисперсия — это статистическое измерение, указывающее разброс между элементами в наборе данных. Вектор Векторы описывают математические величины, которые имеют как величину, так и направление. Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, перемещение и импульс являются векторными величинами. Объем Объем — это трехмерное пространство, занимаемое твердой или полой формой. Количественно это определяется кубическим измерением пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, т.е. м 3 . Дополнительная литература по необходимым навыкам Руководство по необходимым навыкам счета Это руководство, состоящее из четырех частей, знакомит вас с основами счета от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрия и статистика. Если вы хотите освежить свои знания или помочь своим детям в их обучении, эта книга для вас. Математические символы — список символов, примеры решенийМатематика — это числа, символы и формулы. Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
Общие математические символыЕсли мы напишем несколько раз слова «прибавление 4 к 2 дает 6», это может усложнить ситуацию. Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарный запас математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем. Наиболее распространенные символы перечислены в следующей таблице:
Константы, используемые в качестве математических символовМы используем константы в математике для обозначения неизменных объектов. Эти константы могут включать в себя ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (например, единичную матрицу). Эти математические константы чаще всего принимают форму буквы алфавита или ее производной. В следующей таблице перечислены некоторые наиболее часто используемые константы, а также их имена, значения и использование.
Математические символы, используемые в логикеВ следующей таблице показаны математические символы, используемые в логике.
Диаграмма Венна и символы теории множествВ следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.
Цифровые символыЦифровые символы с их примерами и соответствующие индийско-арабские цифры перечислены здесь, в таблице.
Символы геометрии и алгебрыВ приведенной ниже таблице показаны наиболее часто используемые геометрические символы. Математические символы с названиями и примерами также приведены в таблице.
Алгебраические символы В следующей таблице показаны наиболее часто используемые алгебраические символы. \(\neq\) | Не равно | \(a + 5 = b+1 \ подразумевает a \neq b\) | \(=\) | равно | \(а = 5\) | \(\пропто\) Пропорционально | \(x \propto y \имеется в виду x= ky \) | \(f(x)\) | Функция отображает значения \(\)x в \(f(x)\) | \( f(x) = x +3 \) | Греческие алфавиты и символы комбинаторикиВ таблице ниже показаны греческие алфавиты, используемые в качестве математических символов. Их имена, использование и примеры также перечислены в таблице.
Символы комбинаторикиВ таблице ниже показаны наиболее часто используемые символы комбинаторики. 96{P_4} &= 6 \times 5 \times 4 \times 3 = 360\end{align} |
Похожие статьи о математических символах
Ознакомьтесь со следующими страницами, посвященными математическим символам.
- Арифметика
- Алгебраические выражения
- Правила делимости
- Векторы
Важные примечания
Вот несколько моментов, которые следует помнить при изучении математических символов:
- Использование символов для представления информации облегчает понимание математических выражений.

- У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.
- Мы используем константы в математике для обозначения неизменных объектов.
Часто задаваемые вопросы о математических символах
Что такое U в математических символах?
Математический символ U используется для обозначения набора, состоящего из элементов двух наборов. Следовательно, объединение двух множеств P и Q будет множеством элементов P и Q. Для обозначения множества используется специальный символ ∪, который выглядит как «U».
Сколько существует математических символов?
Более 10000 математических символов. Некоторые из основных: =,+,−,≠,±, * и так далее. Есть сложные символы, такие как \(\alpha\), \(\varepsilon\) и так далее.
Какой математический символ используется для обозначения периода волны?
Математический символ, который используется для обозначения периода волны, — λ. Он также известен как длина волны, которая измеряется в единицах расстояния.
Для чего используется математический символ сложения?
Символ сложения (+) обычно используется при сложении двух и более чисел, например, 5 + 5. Кроме того, символ (+) также может использоваться для обозначения положительного числа, например, +7.
Список некоторых распространенных арифметических математических символов.
Некоторые из распространенных арифметических математических символов: знак плюс (+), используемый для сложения, знак минус (-), используемый для вычитания, знак звездочки (*) или знак умножения (×), используемый для умножения, и знак деления (÷). или знак косой черты (/), используемый для деления.
Математические символы
На этой странице собраны статьи о математике из моего недолговечного блога Symbolism. Здесь собраны нематематические посты.
Содержание:
- Функция Weierstrass p
- Повернутые Т-образные
- Кириллические буквы в математике
- постоянная Планка
- Эпи- и монострелы
- Существует
- Длинный S
- равно
- Алеф
Функция Weierstrass p
Математики не часто меняют стиль букв для обозначения специальных функций, но функция Вейерштрасса ℘ является заметным исключением. Этот символ описывается в Unicode как U+2118 (ПРОПИСНАЯ ЗАГЛАВНАЯ P). Он имеет именованный объект HTML
Этот символ описывается в Unicode как U+2118 (ПРОПИСНАЯ ЗАГЛАВНАЯ P). Он имеет именованный объект HTML ℘ . LaTeX для ℘ равен \wp .
Математическое значение функции Вейерштрасса ℘ состоит в том, что все эллиптические функции могут быть выражены как рациональные функции этой функции и ее производных.
Повернутые тройники
Logic использует символ без засечек T (⊤, U+22A4) для обозначения «верно». Тот же перевернутый символ (⊥, U+22A5) используется для обозначения «ложь». Преимущество использования этого символа, а не какой-либо формы F, заключается в том, что он делает симметрию некоторых формул более очевидной.
Логика также использует символы, которые выглядят как T, повернутый на 90° по часовой стрелке или против часовой стрелки, ⊢ (U+22A2) и ⊣ (U+22A3). Выражение x ⊢ y означает, что y доказуемо из х . Точно так же x ⊣ y означает, что x доказуемо из y . Оба выражения вместе используются для эквивалентности, то есть x ⊣⊢ y означает, что x и y доказуемы из другого.
Оба выражения вместе используются для эквивалентности, то есть x ⊣⊢ y означает, что x и y доказуемы из другого.
Символы ⊢ (U+22A2) и ⊣ (U+22A3) — это \vdash и \dashv в LaTeX.
Символы ⊤ (U+22A4) и ⊥ (U+22A5) \top и \bot в LaTeX.
Буквы кириллицы в математике
Я упомянул в разговоре, что в математике редко используются еврейские или русские буквы. Андрес Кайседо указал, что кириллическая буква ша (Ш, U+0428) является исключением. Он используется для группы Тейта–Шафаревича абелева многообразия. Я никогда раньше не слышал о таком.
Буква sha также используется в теории распределения для обозначения «гребенки Дирака» — бесконечной суммы равномерно расположенных дельта-функций. Я видел гребенку Дирака раньше, но не помню, чтобы Ø использовался как ее символ.
Ша, по-видимому, является исключением, подтверждающим правило редкости использования кириллических букв в математике (по крайней мере, на Западе). В Википедии сказано: «Ш отличается тем, что является единственной кириллической буквой, используемой в математике на международном уровне». Также, согласно Википедии, ша, вероятно, происходит от современной еврейской буквы Шин (ש, U+05E9).
В Википедии сказано: «Ш отличается тем, что является единственной кириллической буквой, используемой в математике на международном уровне». Также, согласно Википедии, ша, вероятно, происходит от современной еврейской буквы Шин (ש, U+05E9).
Кстати, фраза «исключение, подтверждающее правило» не имеет смысла в обычном понимании. Если что, исключения опровергают правило. Я думаю, первоначальное понимание этой фразы заключалось в том, что если исключения замечательны, это показывает, что правило часто выполняется.
Постоянная Планка
В физике постоянная Планка — это константа пропорциональности между энергией и частотой частицы: E = ч ν. При работе с угловой частотой ? Символ х произносится просто как «ч бар» и иногда называется приведенной постоянной Планка.
Правильное значение Юникода для h — это U+210E (ПОСТОЯННАЯ ПЛАНКА), а не просто обычное h U+0068 (ЛАТИНСКАЯ СТРОЧНАЯ БУКВА H). Кроме того, в расширенной латинской части Unicode есть символ ħ, U+0127 (СТРОЧНАЯ ЛАТИНСКАЯ БУКВА H С ШТРИХОМ), но правильная кодовая точка для ħ — это U+210F (ПОСТОЯННАЯ ПЛАНКА НАД ДВУМЯ ПИ). Если вам интересно, почему кто-то должен заботиться о проведении таких различий, см. этот пост.
Если вам интересно, почему кто-то должен заботиться о проведении таких различий, см. этот пост.
Команда LaTeX для ħ : \hslash . В LaTeX нет специальной команды для h , потому что он не делает семантических различий между визуально идентичными символами.
Если вы посмотрите на исходный код этой страницы, то увидите, что я намеренно использую неправильные символы для h и ħ . Это потому, что поддержка шрифтов для Unicode плохая. Бьюсь об заклад, что больше людей смогут увидеть глифы для латинских букв, чем для правильных символов.
Эпи- и моно-стрелки
Математики иногда украшают стрелки на диаграммах, чтобы закодировать больше информации о том, что представляет собой стрелка. Эти украшения не совсем стандартные, поэтому мне сложно (по крайней мере мне) запомнить, что они означают.
Функции «один к одному» обозначаются стрелкой с раздвоенным концом. Это U+21A3 или \rightarrowtail в LaTeX. (Их также называют инъективными функциями или мономорфизмами.)
(Их также называют инъективными функциями или мономорфизмами.)
Онто-функции обозначаются стрелкой с двумя концами. Это U+21A0 или \twoheadrightarrow в LaTeX. (Их также называют сюръективными функциями или эпиморфизмами). Если вы знаете значение стрелок выше, вы можете использовать это, чтобы запомнить определения теории категорий. Или, если вы можете вспомнить определения теории категорий, вы можете использовать это, чтобы запомнить значение стрелок.
В теории категорий мономорфизмы определяются с помощью диаграммы с двумя стрелками слева. Вы можете представить, как они превращаются в две линии на хвосте стрелы.
Эпиморфизмы определяются с помощью диаграммы со стрелками справа. Вы можете представить, что эти две стрелки накладываются друг на друга, а затем сдвигаются по горизонтали так, чтобы у вас было два наконечника стрелы.
Существует
В логике обратная буква Е является сокращением от «существует». Этот символ называется «экзистенциальным квантором». Его кодовая точка в Юникоде — U+2203. Команда TeX для создания символа:
Этот символ называется «экзистенциальным квантором». Его кодовая точка в Юникоде — U+2203. Команда TeX для создания символа: \exists .
Есть несколько распространенных вариантов этого символа. Один из них — после символа поставить восклицательный знак, чтобы обозначить, что вещь, существование которой утверждается, уникальна, т. е. вы можете прочитать пару символов как «существует уникальная».
Другой вариант — нарисовать косую черту через символ, чтобы обозначить, что чего-то не существует. Кодовая точка Unicode для этого варианта — U+2204, а команда TeX — \nexists .
Long S
Готфрид Лейбниц использовал начальную букву «s» от summa , что на латыни означает sum , для обозначения интегрирования. Он использовал «длинную S», форму буквы, обычно используемую в его время.
Известным примером длинной буквы S является слово «Конгресс», написанное поверх Билля о правах.
Длинная буква S перестала использоваться в печати вскоре после того, как был написан Билль о правах, хотя она сохранялась в почерке еще несколько десятилетий.
Кодовая точка Unicode для длинной буквы S — U+017F. Кодовая точка для знака интеграла — U+222B.
Равно
Трудно представить математику без знака равенства, но наш символ равенства был придуман совсем недавно относительно истории математики. Роберт Рекорд изобрел этот символ в 1557 году, и он не использовался широко до 1700-х годов. Рекорд использовал параллельные линии, чтобы символизировать равенство, потому что «никакие 2 тона не могут быть более равными».
Значение знака равенства может быть тонким. Мы должны быть осторожны в том, в каком смысле мы считаем вещи с обеих сторон равными. Барри Мазур написал на эту тему сложную статью с обманчиво простым заголовком «Когда одна вещь равна другой?»
Равенство может быть тонким и в языках программирования. Утверждение a = b может означать разные вещи на разных языках. В C это означает поместить значение b в адрес и . В Python это означает присвоение имени a значению b . В C++ оператор присваивания может быть перегружен, поэтому
В C++ оператор присваивания может быть перегружен, поэтому a = b может привести к выполнению произвольного кода. В функциональном языке программирования a = b означает постоянное присвоение значения b a . На других языках это означает, что a содержит или ссылается на значение b на данный момент .
Алеф
Единственная еврейская буква, обычно используемая в математике, — это алеф, א, первая буква еврейского алфавита. Он используется с нижними индексами для обозначения мощности различных бесконечных множеств. Чаще всего используется с нижним индексом 0, произносимым как «алеф ноль» или «алеф нуль», для обозначения мощности целых чисел. Неудивительно, что команда TeX для алефа имеет вид \aleph .
При использовании в качестве буквы иврита ее кодовая точка Unicode (U+05D0). При использовании в качестве математического символа он имеет четкую кодовую точку U+2135. Я ожидал, что алеф ноль (ℵ 0 ), чтобы иметь собственное значение Unicode, но, похоже, это не так.
Я ожидал, что алеф ноль (ℵ 0 ), чтобы иметь собственное значение Unicode, но, похоже, это не так.
א часто транслитерируется алеф на конце; Википедия, например, следует этому соглашению. Однако стандарт Unicode использует алеф для буквы и множество ее вариаций.
***
Я никогда не использовал буквы иврита в HTML до написания этого поста, и, очевидно, мне нужно кое-что узнать о HTML и о WordPress. Вот небольшой HTML-файл, который я создал, введя букву алеф тремя способами: как объект HTML, используя значение Unicode и непосредственно введя букву:
Вот как это отображается в моем браузере:
Я удивлен, что ввод escape-последовательностей HTML для алеф дает другой результат, чем прямой ввод символа алеф. И я удивлен, что א0 помещает нижний индекс слева, а א0 помещает нижний индекс справа.
Когда я вставляю тот же код в WordPress, я вижу следующее:
Теперь экранированное значение Unicode и прямой ввод символа дают тот же результат, но объект HTML ℵ дает более крупный символ. Также нижний индекс последнего элемента переместился с правой стороны на левую.
Также нижний индекс последнего элемента переместился с правой стороны на левую.
(Скриншоты выше были взяты из Firefox, работающего в Ubuntu. Я получаю аналогичные результаты в Windows, используя Firefox или Internet Explorer, за исключением того, что א и ℵ отображаются разными шрифтами.)
Не мог бы кто-нибудь оставить комментарий, объясняющий, почему три разных способа ввода алефа используют разные шрифты и следуют разным правилам подстрочных индексов? Спасибо.
Обновление : я предположил, что объект HTML ℵ — это сокращение от еврейской буквы алеф, но это сокращение от математического символа алеф. Это объясняет различное поведение подписки. Кроме того, думал, что набор символов по умолчанию для HTML был UTF-8. Но когда я явно добавляю в мой HTML-файл. Я получаю ожидаемые результаты, т. е. א и א работают одинаково.
Вставка математических символов
Word для Microsoft 365 Word 2021 Word 2019 Word 2016 Word 2013 Word 2010 Word 2007 Дополнительно. .. Меньше
.. Меньше
В Word можно вставлять математические символы в уравнения или текст с помощью инструментов для работы с формулами.
На вставке , в группе Символы щелкните стрелку под Уравнение , а затем щелкните Вставить новое уравнение .
В разделе Equation Tools на вкладке Design в группе Symbols щелкните стрелку More .
Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.

Щелкните символ, который вы хотите вставить.
Доступные наборы символов
Следующие наборы математических символов доступны в группе Символы в Word. Щелкнув стрелку Еще , щелкните меню в верхней части списка символов, чтобы увидеть каждую группу символов.
Набор символов | Подмножество | Определение |
|---|---|---|
Базовая математика | Нет | Часто используемые математические символы, такие как > и < |
Греческие буквы | Нижний регистр | Строчные буквы греческого алфавита |
Верхний регистр | Заглавные буквы греческого алфавита | |
Буквенные символы | Нет | Символы, напоминающие буквы |
Операторы | Общие бинарные операторы | Символы, действующие на две величины, например + и ÷ |
Общие реляционные операторы | Символы, выражающие связь между двумя выражениями, например = и ~ | |
Основные N-арные операторы | Операторы, действующие в диапазоне переменных или терминов | |
Расширенные бинарные операторы | Дополнительные символы, действующие на две величины | |
Расширенные реляционные операторы | Дополнительные символы, выражающие отношение между двумя выражениями | |
Стрелы | Нет | Символы, указывающие направление |
Отрицание отношений | Нет | Символы, выражающие обратную связь |
Скрипты | Скрипты | Математический шрифт Script |
Фрактурс | Математический шрифт Fraktur | |
Двойной удар | Математический шрифт с двойным ударом | |
Геометрия | Нет | Часто используемые геометрические символы |
См.
 также
такжеВставьте галочку или другой символ
158.199 Icon Mathematics Стоковые фото, картинки и изображения
Студент математики, ripped paper, education concept. рваная бумага, стилизованная под мужскую голову с фрагментами разорванной бумаги с математическими символами, формулами и заметками. вектор доступен.
Группа детей на иллюстрации значка математики
Стебель образования вектор красочная рамка с темным фоном
Научные формулы и расчеты в физике и математике на доске. урок алгебры и геометрии в школе. образование и наука. гравировка от руки в старом эскизе и винтажном стиле
Знак «плюс» на векторной иллюстрации талисмана
Взрыв завитка цифр. водоворот объекта, созданный из разбросанных цифр символов. стиль векторной иллюстрации — плоские знаковые символы.
Вектор веб-иконки калькулятора
Круглая иконка знака умножения с теплым градиентом
Основные математические символы равны больше, чем значок на белом фоне. плоский стиль. математический значок для дизайна вашего веб-сайта, логотипа, приложения, пользовательского интерфейса. математический символ.
плоский стиль. математический значок для дизайна вашего веб-сайта, логотипа, приложения, пользовательского интерфейса. математический символ.
Баннер понятий математики. презентация, сайт. изолированная идея типографики букв с линейными иконками. алгебра, геометрия, статистика, базовая математика. векторная иллюстрация контура
Математическая иконка на белом фоне. плоский стиль. значок математики и числа для дизайна вашего веб-сайта, логотипа, приложения, пользовательского интерфейса. символ математических расчетов. знак математических расчетов.
Лампа с математической идеей
Черная сигма в верхнем регистре, выделенная на белом фоне
Набор векторных значков школьных предметов в стиле глифа
Основные математические символы на белом фоне
Безграничный знак. символ бесконечности на белом фоне
Векторная иллюстрация числа Пи. плоский дизайн.
Векторная иллюстрация математических символов и чисел
Текст с вдохновляющей фразой «Я люблю математику» в форме сердца. нарисованная вручную векторная иллюстрация на зеленом фоне.
нарисованная вручную векторная иллюстрация на зеленом фоне.
Концепция математики со школьными уроками в векторной иллюстрации в стиле ретро-мультфильма
Вычитание с крутой градиентной отделкой Круглая иконка с прохладной градиентной отделкой
Знак бесконечности, созданный синим неоновым замораживающим светом на черном фоне
Математика, круглая плоская иллюстрация с математическим символом.
Значок цвета математических символов. меньше, больше или равно знакам. изолированная векторная иллюстрация
Математическое дерево. иллюстрации цифр, изолированные на белом фоне.
Набор прозрачных цветов реалистичных геометрических фигур с изолированными геометрическими объектами разного цвета на прозрачном фоне.
Школьные математические символы в плоском стиле значок
Геометрические линейки и карандаши образовательные принадлежности школьная векторная иллюстрация
Значок символа пи черного цвета в круглой векторной иллюстрации
Плюс меньше векторной иконки, изолированной на прозрачном фоне, плюс меньше логотипа
Набор из дети держат иллюстрацию математических инструментов
Снова в школу элементы, набор векторных иконок, плоский дизайн иллюстрации.
Теория математики и математическая формула уравнение каракули почерк значок на белом изолированном фоне с нарисованной вручную моделью, используемой для школьного образования и оформления документов, создать по вектору
Больше, чем вектор значка знака, выделенный на белом фоне для дизайна вашего веб и мобильного приложения, больше, чем концепция логотипа знака
Монохромный бесшовный узор с книгами, символами и калькуляторами.
Значок суммирующего глифа. сумма или общий математический символ.символ силуэта. негативное пространство. векторная изолированная иллюстрация
Знак образования парового ствола. наука технология инженерное искусство математика.
Набор современных иконок тонкой линии для математики. иллюстрация с различными элементами по теме математики.
Набор мультяшных иконок, на которых изображены рабочие человечки с математическими символами. нарисуйте милые миниатюрные сцены рабочих со знаками алгебры. нарисованная вручную векторная иллюстрация для школьного дизайна и инфографики.
Доска со словом
Дерево рисунков с математическими символами для вашего дизайна
Математические и геометрические значки и формулы на желтых памятках
Значки данных, значки графиков, значки диаграмм
Модный прозрачный стиль. другое направление математики.
Математическая круглая плоская векторная современная иллюстрация. красочный символ математики на белом фоне
Математические символы. набор красочных плоских математических иконок с длинными тенями. суммирование, универсальная квантификация, произведение, интеграл, бесконечность, факториал, экзистенциальная квантификация, пустое множество, знак пи.
Набор мультяшных иконок из эскизов рабочих человечков с математическими символами. нарисуйте милые миниатюрные сцены рабочих со знаками алгебры. нарисованная вручную векторная иллюстрация для школьного дизайна и инфографики.
Основные математические символы. векторная иллюстрация.
Ручная гравировка в старинном эскизе и винтажном стиле. научные формулы и расчеты по физике и математике, химии и биологии или астрономии на доске. образование и наука.
научные формулы и расчеты по физике и математике, химии и биологии или астрономии на доске. образование и наука.
Основные математические символы.
Математические символы
Студент математики. стилизованный мужской силуэт головы с математическими символами и книгами на голове, символизирующими сотейник.
Язык высунут, значок многократного знака изолирован на талисмане
Математические символы
Иллюстрация математического слова в основе — наука, технология, инженерия, математическое образование, концепция типографики, дизайн с элементами орнамента значка
Математический фон значка
Иллюстрация калькулятора, мультяшного человека, показывающего большие пальцы и математические символы
Основные цветные математические символы; плюс, минус, умножение и деление
Мультяшное изображение символа пи
Современная цветная тонкая линия концепции математики для школы, университета и обучения. иллюстрация с различными элементами по теме математики. концепции модного дизайна.
концепции модного дизайна.
Основные цветные математические символы равно меньше больше
Знак греческой буквы Пи. вектор. белый значок с мягкой тенью на прозрачном фоне.
Художественное дерево с математическими символами для вашего дизайна
Силуэт плоского образования Академическая икона для многих предметов, таких как математика, наука, искусство, химия, физика, спорт и инструмент компьютерных технологий, созданный вектором иллюстрация со словами
Пи с числами Пи в круге
Коллекция икон школы и образования на белых кнопках. векторная иллюстрация.
Математические символы на доске
Математические значки
Набор школьных цветных плоских значков. элегантный стильный дизайн
Иллюстрация набора красочных трехмерных математических символов или знаков
Набор математических иконок — векторная геометрия, алгебраические и математические символы или элементы логотипа в стиле тонких линий
Наклейки с математическими символами
Пакет векторных иконок — синяя серия, математическая коллекция
Иконка кристалла квадратного корня, выделенная на белом фоне.
Математический символ в лампочке
Математический символ
Креативная концепция письма
Пакет векторных иконок — синяя серия, математическая коллекция шаблон. образование фон.
Яркие, яркие математические символы (сложение, вычитание, умножение, знаки деления, символы, отметки)
Зеленые и черные иконки с отражением
Коллекция векторных иконок образования. естественные и математические науки, дополнительное образование, репетиторство, фриланс. набор плоских знаков и символов для Интернета и приложений.
Математические иконки и формулы на школьной доске — иллюстрация
Векторная концепция. текстурированный фон. наук и искусств. обратно в школу иконы. функции левого и правого полушарий.
Доска с научными формулами и расчетами по физике и математике. может иллюстрировать научные темы, связанные с квантовой механикой, теорией относительности и любой векторной иллюстрацией научных расчетов.
Векторный фон доски по математике
Значок математики на красном ретро-ракетном дерьме иллюстрации
Векторный набор математики и геометрии
Набор иконок по математике в виде графика eps10
Креативная концепция образования.

 15KB
15KB 34KB
34KB 21KB
21KB В каждой клетке — 1 овал). Затем можно попросить ребенка записать в числовом виде все примеры (можно на отдельном листе).
В каждой клетке — 1 овал). Затем можно попросить ребенка записать в числовом виде все примеры (можно на отдельном листе).  Затем ребенок должен ответить на вопрос, в каком прямоугольнике четное число зверей, а в каком нечетное? Поставить между двумя прямоугольниками правильный математический знак.
Затем ребенок должен ответить на вопрос, в каком прямоугольнике четное число зверей, а в каком нечетное? Поставить между двумя прямоугольниками правильный математический знак.
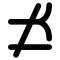 mn$ нечетно, то и $m$, и $n$ нечетны.
mn$ нечетно, то и $m$, и $n$ нечетны. 2) = g(3,1) + 5$
2) = g(3,1) + 5$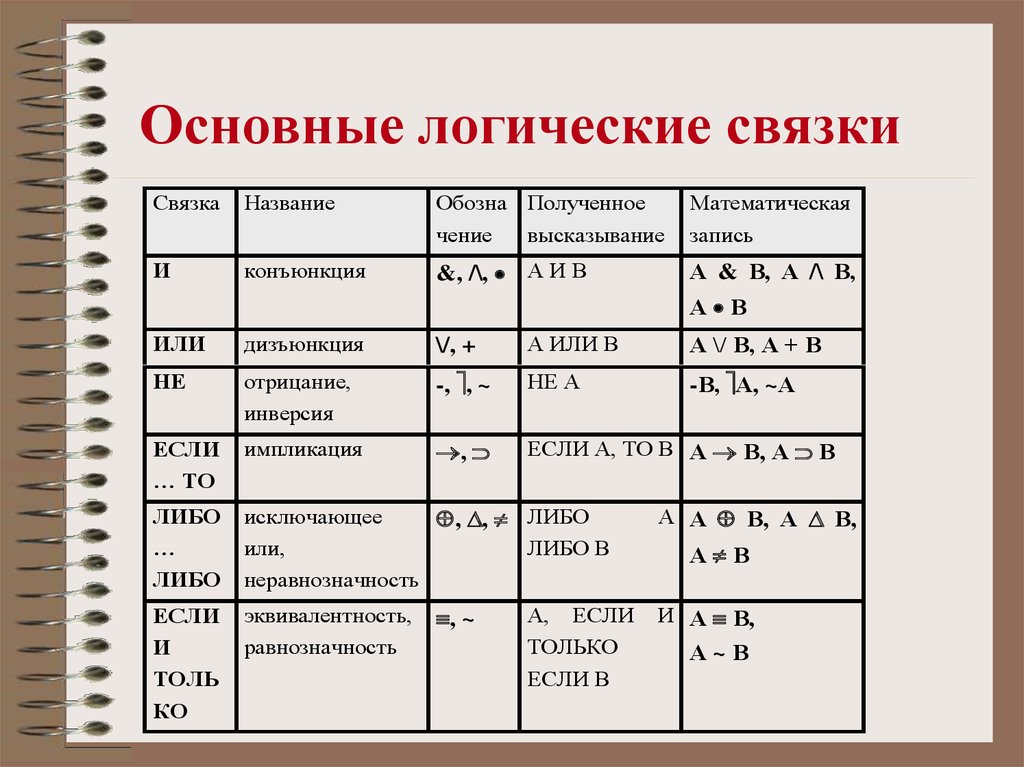 9004
9004
 в разделе , связанные с функциями символы .
в разделе , связанные с функциями символы . $
$ $
$ \overline{3}$
\overline{3}$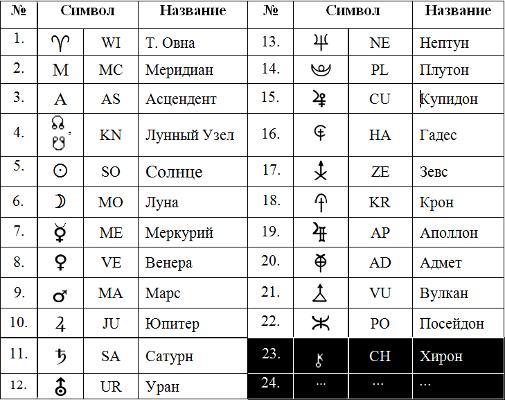 $p$
$p$
 = 2x$
= 2x$ в разделе символы геометрии и тригонометрии .
в разделе символы геометрии и тригонометрии . что $P(A \cap B) = P(A)P(B).$
что $P(A \cap B) = P(A)P(B).$ $\,\blacksquare$
$\,\blacksquare$
 ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.  Две стороны отношения, обозначенные этим символом, будут , а не быть достаточно точным для математической обработки.
Две стороны отношения, обозначенные этим символом, будут , а не быть достаточно точным для математической обработки.
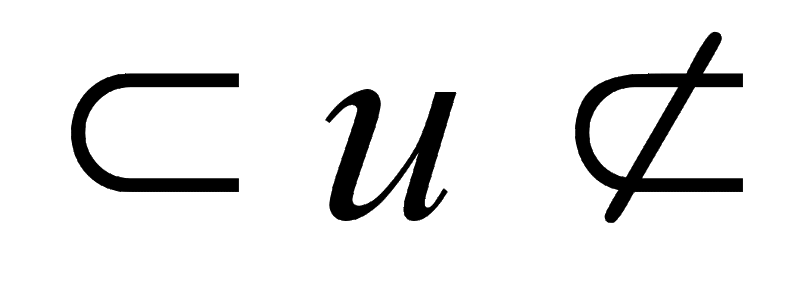
 Запятая разбивает большие числа на блоки из трех цифр.
Запятая разбивает большие числа на блоки из трех цифр.
 Линия перпендикулярна (под прямым углом) к стороне.
Линия перпендикулярна (под прямым углом) к стороне. Обычно он помещается перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная.
Обычно он помещается перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная. Это относится к расширению графика, кривой или диапазона значений до диапазона, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.
Это относится к расширению графика, кривой или диапазона значений до диапазона, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.
 Пропорция связана с дроби .
Пропорция связана с дроби . Один радиан эквивалентен углу, образуемому в центре окружности дугой, длина которой равна радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Один радиан эквивалентен углу, образуемому в центре окружности дугой, длина которой равна радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан. е. это мера вариации или разброса набора значений. Там, где разброс данных низкий и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону
е. это мера вариации или разброса набора значений. Там, где разброс данных низкий и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону

 \)
\)
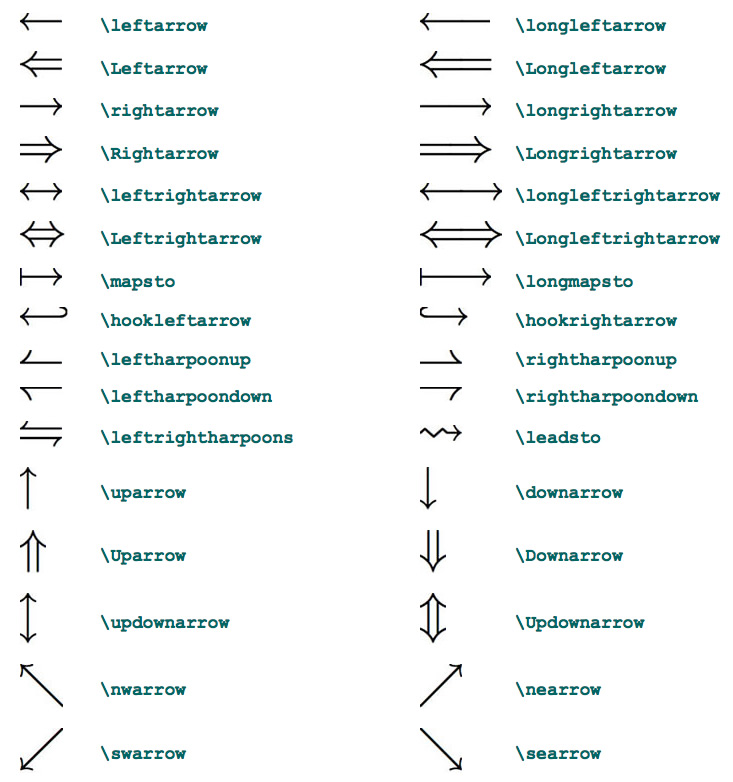 ..}
..}
 …
… 2 \)
2 \)

