| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . 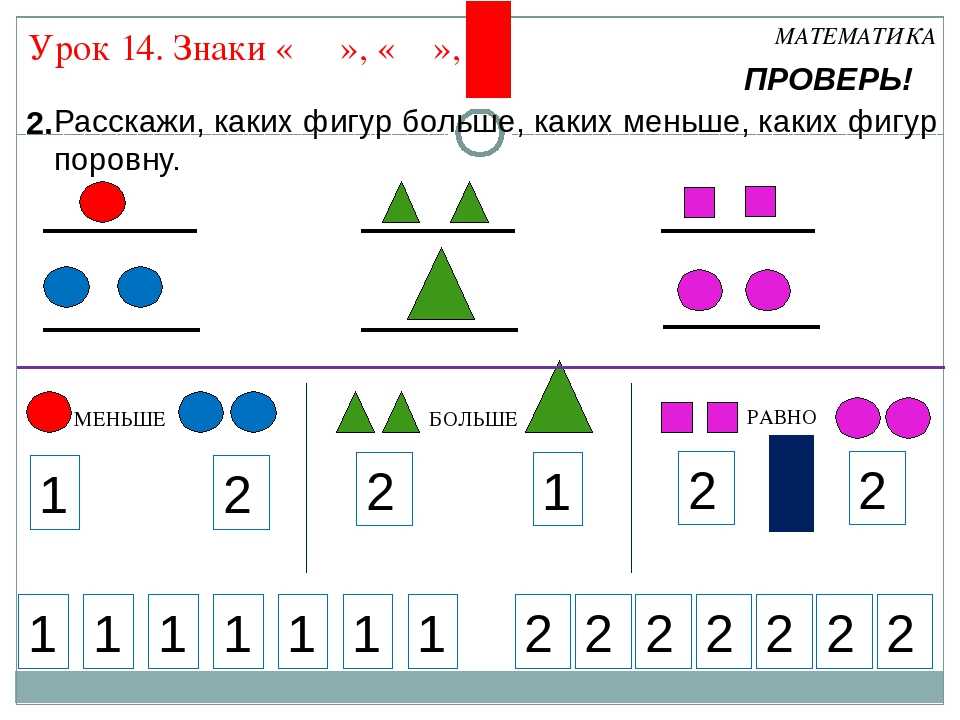 Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
Знаки больше, меньше или равно в математике
Поможем понять и полюбить математику
Начать учиться
1096.5K
С детства нам понятно, что три шоколадки больше одной, но записывать это в виде формулы мы учимся только в первом классе школы. В этом материале рассмотрим математические знаки и способы их запоминания.
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук.
Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Строгие неравенства — используют только знак больше (>) или меньше (<).
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- неравенства a > b и b < a означают одно и то же, то есть равносильны.
Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
Другие типы неравенств.
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Онлайн-курсы по математике для детей помогут быстрее разобраться в математических символах и закрепить знания на практике с опытными преподавателями.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Таблица умножения: поможем выучить легко и быстро
К следующей статье
396.6K
Как находить проценты от числа
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
базовых математических символов | Словарь
математика (BrE) | математика (AmE) является сокращенной формой математика
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.
плюс/дополнение
Знак плюс означает:
а. понятие
положительноеЛюбое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — одно и то же число.
б. операция сложения
3 + 5 = 8
три плюс пять равно восьми
пять прибавить к трем, получится восемь
три прибавить к пяти, получится восемь
Сложение дает нам сумму . В 3 + 5 = 8 сумма равна восьми.
—
знак минус/знак вычитания
Знак минус означает:
а. понятие отрицательного
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3
минус три
б. операция вычитания
8 — 5 = 3
восемь минус пять равно трем
пять вычесть из восьми равно трем
если из восьми вычесть пять, то получится три
если из восьми вычесть пять, то получится три
Вычитание дает нам разницы .
В 8 — 5 = 3 разница три.
×
знак умножения / знак умножения
Знак умножения на означает:
умножение 5 x 6 = 30
пять раз шесть равно тридцати
пять умножить на шесть равно тридцати
пять шестерок равно тридцати
если умножить 5 на 6 получится тридцать
Умножение дает нам произведение . В 5 х 6 = 30 произведение равно 30.
÷ ИЛИ /
знак деления
Знак деления представляет:
подразделение
15 ÷ 3 = 5
15 / 3 = 5
пятнадцать разделить на три равно пяти
пять получится пятнадцать трижды
если пятнадцать разделить на три получится пять
если три разделить на пятнадцать получится пять
дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.
Подытожим вышеописанные четыре операции следующим образом:
| операция | результат | ||
|---|---|---|---|
| дополнение | «плюс» | 2 + 2 = 4 | сумма |
| вычитание | «минус» | 5 — 3 = 2 | разница |
| умножение | «раз» | 3 х 5 = 15 | товар |
| отделение | «делится на» | 21/7 = 3 | частное |
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7
три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно НЕ равно:
- два плюс два равно четыре
-
два плюс два равно четырем
меньше
3 < 4
три меньше четырех
>
больше
4 > 3
четыре больше трех
≠
НЕ равно
x ≠ z
x не равно z
≥
больше или равно
x ≥ z
x больше или равно z
≤
меньше или равно
z ≤ x
z меньше или равно x
¾
дробь
см.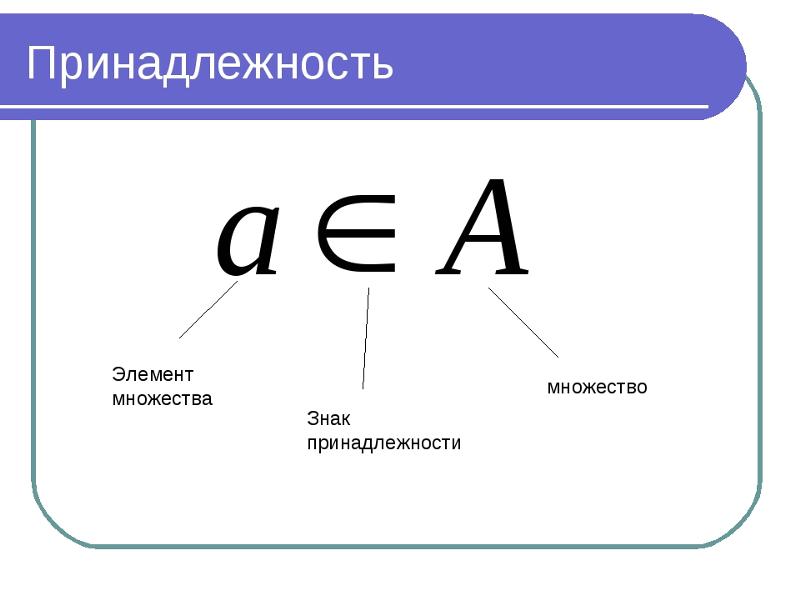
дроби
.
десятичный разделитель | точка
Десятичный разделитель отделяет целое число от его дробной части справа:
1,23
В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).
см. десятичные дроби
,
разделитель тысяч
В английском языке разделитель тысяч разделяет целые числа на группы по три справа.
10 987 654 321
В английском языке разделителем тысяч обычно является запятая (,). Обратите внимание, что в некоторых языках разделителем тысяч является точка (.), а иногда и пробел ( ).
см. тыс.
%
знак процента
Знак процентов указывает число или отношение в виде доли от 100 ( процентов ).
40%
сорок процентов
Только сорок процентов людей проголосовали за нее.
Какой процент проголосовал за нее? Сорок процентов.
√
квадратный корень
√16 = 4
квадратный корень из шестнадцати равен четырем
квадратный корень из шестнадцати равен четырем
Математические символы — список символов, примеры решения
Математика — это числа, символы и формулы. Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
| 1. | Общие математические символы |
| 2. | Константы, используемые в качестве математических символов |
| 3. | Математические символы, используемые в логике |
| 4. | Диаграмма Венна и символы теории множеств |
5. | Цифровые символы |
| 6. | Символы геометрии и алгебры |
| 7. | Греческие алфавиты и символы комбинаторики |
| 8. | Решенные примеры |
| 9. | Практические вопросы |
| 10. | Часто задаваемые вопросы о математических символах |
Общие математические символы
Если мы напишем несколько раз слова «прибавление 4 к 2 дает 6», это может усложнить ситуацию. Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарный запас математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем. Наиболее распространенные символы перечислены в следующей таблице:
| Символы | Значение | Примеры математических символов |
|---|---|---|
| + | Добавить | 5 + 4 = 9 |
| — | Вычесть | 5 — 4 = 1 |
| = | равно | 1+1 = 2 |
| \(\экв\) | Тождественно равно | (а+б) 2 \(\экв\) а 2 + 2аб +б 2 |
| \(\примерно\) | Приблизительно равно | \(\пи \приблизительно 3,14\) |
| \(\neq\) | Не равно | 5 + 4 \(\neq\) 1 |
| \(\раз\) | Умножить | 5 \(\раз\) 4 = 20 |
| \(\дел\) | Разделить | 10 \(\дел\) 2 = 5 |
| \(<\) | Менее | 10 \(<\) 20 |
| \(>\) | Больше | 20 \(>\) 10 |
| \(\leq\) | Меньше или равно | х + у \(\leq\) г |
| \(\geq\) | Больше или равно | х + у \(\geq\) г |
| \(\%\) | Процент | 50% = \(\begin{align}\frac{50}{100}\end{align}\) |
\(. \) | Десятичная точка или период | \(\begin{align}\frac{1}{2} = 0,5\end{align}\) |
| \(-\) | Винкулум Разделяет числитель и знаменатель | \(\begin{align}\frac{2}{3}\end{align}\) |
| \( \sqrt{} \) | Квадратный корень | \(\sqrt{4} = 2\) |
| \(\sqrt[3]{х}\) | Кубический корень из x | \( \sqrt[3]{ 27} = 3\) |
| \( \sqrt[n]{x}\) | n th корень \(x\) | \( \sqrt[4]{16} = 2\) |
| \(()\) | Скобки | \(2+(5-3) = 2 +2 = 4\) |
| \([\:\:]\) | Квадратные скобки | \(\ начало {выравнивания} &3\раз[2 +(5 -2)] +1 \\ &3 \раз[2+3] +1 \\ &3 \times5+1\\ &16 \конец{выравнивание}\) |
| \(\{\}\) | Кронштейн для цветов | \(\ начало {выравнивания} &16 \div \{3\times[2 +(5 -2)] +1\} \\ &16 \дел \{3 \раз[2+3] +1\} \\ &16 \дел \{3 \times5+1\}\\ &16 \дел \{16\} \\ &1 \конец{выравнивание}\) |
| \(\в\) | Принадлежит | 0 \(\in\) Целое число |
| \(\нет\в\) | Не принадлежит к | \(\frac{1}{2} \not\in\) Натуральные числа |
| \(\поэтому\) | Поэтому | \(x+1 = 2 \следовательно, x = 1\) |
| \(\потому что\) | Потому что | \(\begin{align}\frac{1}{2} \!\div\! 0,5 \!= \!1 (\потому что\! \frac{1}{2} \!=\! 0,5)\ конец{выравнивание}\) |
| \(\infty\) | Бесконечность | Бесконечность бесчисленна, \(\begin{align}\frac{1}{3}\end{align}\) при записи в десятичной форме, бесконечно \(0,333. |
| \(!\) | Факториал | \( 5!\ \!\!=\! 5 \!\раз\! 4 \!\раз\!3 \!\раз\! 2\! \раз\! 1\) |
….\)Константы, используемые в качестве математических символов
Мы используем константы в математике для обозначения неизменных объектов. Эти константы могут включать в себя ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (например, единичную матрицу). Эти математические константы чаще всего принимают форму буквы алфавита или ее производной. В следующей таблице перечислены некоторые наиболее часто используемые константы, а также их имена, значения и использование.
| Имя символа | Пояснение |
|---|---|
| 0 (ноль) | Аддитивная идентичность общих чисел |
| 1 (один) | Мультипликативная идентичность обычных чисел |
| √2 (квадратный корень из 2) | Положительное число, квадрат которого равен 2.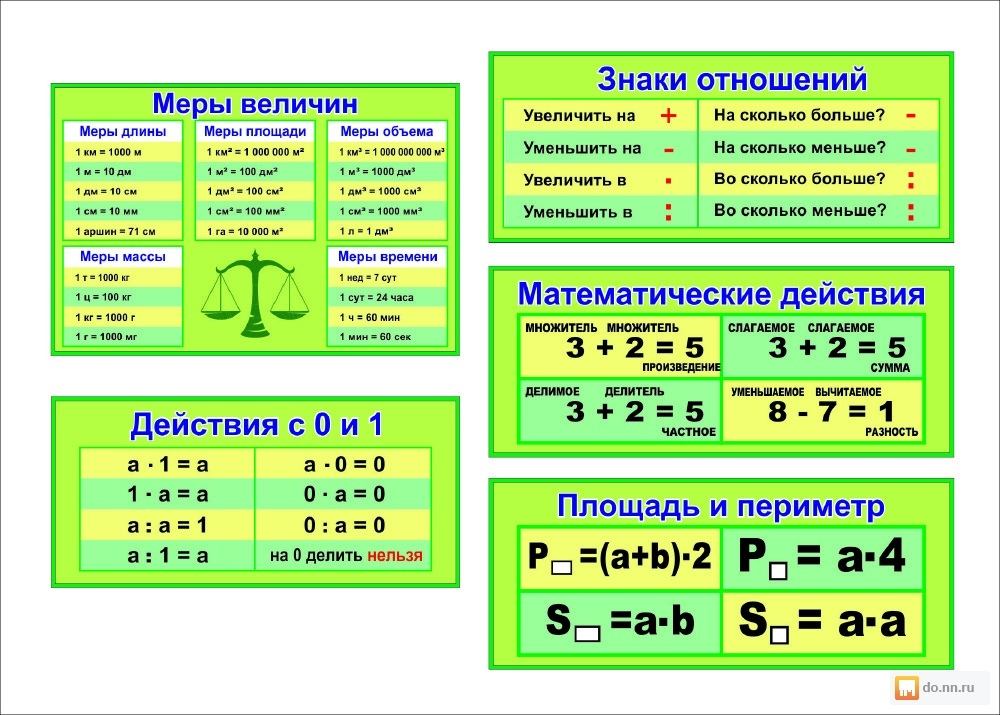 Приблизительно равно 1,41421. |
| e (постоянная Эйлера) | Основание натурального логарифма. Предел последовательности (1 + (1/n) n ). Приблизительно равно 2,71828 |
| \(\pi\) (Pi, постоянная Архимеда) | Отношение длины окружности к ее диаметру. Половина окружности единичного круга. Приблизительно равно 3,14159 |
| \( \phi\) (Phi, золотое сечение) | Отношение между большим числом и p меньшим числом q, когда (p+q)/p = p/q. Положительное решение уравнения y 2 -y-1 = 0 . |
| i (Воображаемая единица) | Главный корень из -1. Основной компонент комплексного числа. |
Математические символы, используемые в логике
В следующей таблице показаны математические символы, используемые в логике.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\существует\) | Существует по крайней мере один | ∃ х: Р(х)∃ х: F(х) Существует хотя бы один элемент p(x), \(x\), , такое что F(x) равно True. |
| \(\существует!\) | Существует один и только один | ∃! х: Ф(х) означает, что существует ровно один \(x\) такое, что F(x) истинно. 92 > 1\) |
| \(\отриц\) | Логический Не | Утверждение A истинно, только если \(\neg\) ложно \(х \neq y \iff\neg(x=y)\) |
| \(\лор\) | Логическое ИЛИ | Утверждение A \(\lor\) B верно , если A или B верно; , если оба ложны, утверждение неверно. |
| \(\земля\) | Логический И | Утверждение A \(\land\) B истинно , если A и B оба верны; иначе это ложь. |
| \(\подразумевается\) | Подразумевается | х = 2 \(\подразумевается\) x 2 = 4 |
| \(\если\) | Если и только если | х +1 = у +1 \(\ тогда и только тогда) х = у |
| \(\text{|}\) или \(\text{:}\) | Такой, что | { \(х\) | \(х\) > 0} = {1,2,3,. ..} |
Диаграмма Венна и символы теории множеств
В следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\крышка\) | Перекресток | А = {2,3,4} Б = {4,5,6} А \(\крышка\) В = {4} |
| \(\чашка\) | Союз | А = {2,3,4} В = {4,5,6} А \(\чашка\) В = {2,3,4,5,6} |
| \(\ничего\) | Пустой набор | Набор без элементов \(\varnothing\) = { } |
| \(\в\) | Является членом | 2 \(\в\) \(\mathbb{N}\) |
| \(\нотин\) | не является членом | 0 \(\нетин\) \(\mathbb{N}\) |
| \(\подмножество\) | Является подмножеством | \(\mathbb{N} \подмножество \mathbb{I}\) |
| \(\расстроен\) | Является надмножеством | \(\mathbb{R} \supset \mathbb{W}\) |
| \(\текст{П(А)}\) | Силовой набор А | P({1,2}) = {{}, {1}, {2}, {1,2}} |
| \(А=В\) | Равенство (одинаковые элементы в наборе А и наборе В) | А = {1,2}; В = {1,2} \(\ подразумевает \) А = В |
| \( А \раз В\) | Декартово произведение Набор заказанных пар из A и B | А ={5,6}; В = {7,8} \(\ подразумевает \)\( A \times B\) = {(5,7),(5,8),(6,7),(6,8)} |
| \(\текст{|А|}\) | Количество элементов в множестве A | |{1,2,3,4}| = 4 |
Цифровые символы
Цифровые символы с их примерами и соответствующие индийско-арабские цифры перечислены здесь, в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| Римская цифра I | Значение = 1 | I = 1 , II = 2 , III = 3 |
| Римская цифра V | Значение = 5 | IV = 4 (5-1) ВИ = 6 (5+1) VII = 7 (5+2) VIII = 8 (5+3) |
| Римская цифра X | Значение = 10 | IX = 9 (10-1) |
| Римская цифра L | Значение = 50 | XLIX = 49 (50-1) |
| Римская цифра C | Значение = 100 (столетие) | СС = 200 (100+100) CCLIX = 259 (100+100+50+9) |
| Римская цифра D | Значение = 500 | DCLI = 651 (500+100+50+1) DCCIV = 704 (500+100+100+4) |
| Римская цифра M | Значение = 1000 | ММ = 2000 (1000+1000) |
| R или \(\mathbb{R}\) | Вещественные числа | \(\frac{1}{2} , \frac{1}{4}, 0,5\)\(\sqrt{2},\sqrt{3}\) |
| Z или \(\mathbb{Z}\) | Целое число | -100,-20,5,10,. … |
| N или \(\mathbb{N}\) | Натуральные числа | 1,2,3,…500,… |
| Q или \(\mathbb{Q}\) | Рациональные числа | \(-\frac{1}{2}, \frac{1}{4}, 0,5\) |
| P или \(\mathbb{P}\) | Иррациональные числа | \(\sqrt{2},\sqrt{3}\) |
| C или \(\mathbb{C}\) | Комплексные числа | 5+2i |
Символы геометрии и алгебры
В приведенной ниже таблице показаны наиболее часто используемые геометрические символы. Математические символы с названиями и примерами также приведены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\угол\) | Укажите угол | \(\угол ABC\) |
| \(\Дельта\) | Символ треугольника | \(\Дельта\текст{PQR}\) |
| \(\конг\) | соответствует | \(\Delta \text{PQR} \cong \Delta \text{ABC}\) 9\цирк\) |
| \(\overline{\rm AB}\) | Отрезок линии AB | Линия из точки А в точку Б |
| \(\overrightarrow{\rm AB}\) | Рэй AB | Линия, начинающаяся из точки А и продолжающаяся через точку В |
| \(\overleftrightarrow{\rm AB}\) | Линия AB | Бесконечная линия, проходящая через точки A и B | 9в\)
Алгебраические символы
В следующей таблице показаны часто используемые алгебраические символы.
2 \)
\(\пропто\)
Греческие алфавиты и символы комбинаторики
В таблице ниже показаны греческие алфавиты, используемые в качестве математических символов. Их имена, использование и примеры также перечислены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\альфа\) | Альфа | Используется для обозначения углов, коэффициентов |
| \(\бета\) | Бета | Используется для обозначения углов, коэффициентов |
| \(\гамма\) | Гамма | Используется для обозначения углов, коэффициентов |
| \(\Дельта\) | Дельта | Дискриминантный символ |
| \(\варепсилон\) | Эпсилон | Используется для обозначения универсального набора |
| \(\йота\) | Йота | Представляет мнимое число |
| \(\лямбда\) | Лямбда | Представляет константу |
| \(\пи\) | Пи | \(\пи \примерно 3,14\) |
| \(\Сигма\) | Сигма | Представляет сумму |
| \(\тета\) | Тета | Представляет углы |
| \(\ро\) | Ро | Статистическая константа |
| \( \фи\) | Фи | Обозначение диаметра |
Символы комбинаторики
В таблице ниже показаны наиболее часто используемые символы комбинаторики.
96{P_4} &= 6 \times 5 \times 4 \times 3 = 360\end{align}
Похожие статьи о математических символах
Ознакомьтесь со следующими страницами, посвященными математическим символам.
- Арифметика
- Алгебраические выражения
- Правила делимости
- Векторы
Важные примечания
Вот несколько моментов, которые следует помнить при изучении математических символов:
- Использование символов для представления информации облегчает понимание математических выражений.
- У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.
- В математике мы используем константы для обозначения неизменяющихся объектов.
Часто задаваемые вопросы о математических символах
Что такое U в математических символах?
Математический символ U используется для обозначения набора, полученного путем объединения элементов двух наборов.
Следовательно, объединение двух множеств P и Q будет множеством элементов P и Q. Для обозначения множества используется специальный символ ∪, который выглядит как «U».
Сколько существует математических символов?
Более 10000 математических символов. Некоторые из основных: =,+,−,≠,±, * и так далее. Есть сложные символы, такие как \(\alpha\), \(\varepsilon\) и так далее.
Какой математический символ используется для обозначения периода волны?
Математический символ, который используется для обозначения периода волны, — λ. Он также известен как длина волны, которая измеряется в единицах расстояния.
Для чего используется математический символ сложения?
Символ сложения (+) обычно используется при сложении двух и более чисел, например, 5 + 5. Кроме того, символ (+) также может использоваться для обозначения положительного числа, например, +7.
Перечислите некоторые распространенные арифметические математические символы.
Некоторые из распространенных арифметических математических символов: знак плюс (+), используемый для сложения, знак минус (-), используемый для вычитания, знак звездочки (*) или знак умножения (×), используемый для умножения, и знак деления (÷).