Действие противодействие: Законы Ньютона — Википедия – Третий закон Ньютона — Википедия

Законы Ньютона — Википедия

Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)^[1][2]. В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.

Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность^[3]) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.

Современная формулировка[править | править код]

В современной физике первый закон Ньютона принято формулировать в следующем виде^[4]:

Историческая формулировка[править | править код]

Ньютон сформулировал первый закон механики так:

Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[5][6][7][8].

Современная формулировка[править | править код]

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}

где a→{\displaystyle {\vec {a}}} — ускорение материальной точки;
F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m} — масса материальной точки.

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},}

где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени

[9]^[10][11].

Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}} и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[12][13].

Замечания[править | править код]

Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:

ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}

или

dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}

Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0}) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка[править | править код]

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Этот закон описывает, как взаимодействуют две материальные точки. Пусть имеется замкнутая система, состоящая из двух материальных точек, в которой первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}}, а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}}. Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}}.

Третий закон Ньютона является следствием однородности, изотропности и зеркальной симметрии пространства^[14][15].

Третий закон Ньютона, как и остальные законы ньютоновской динамики, даёт практически верные результаты лишь только тогда, когда скорости всех тел рассматриваемой системы пренебрежимо малы по сравнению со скоростью распространения взаимодействий (скоростью света)^[16].

Современная формулировка[править | править код]

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.}

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно^[17].

Историческая формулировка[править | править код]

Ньютон дал следующую формулировку закона^[1]:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[18][19].

Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.

Уравнения движения[править | править код]

Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Закон сохранения импульса[править | править код]

Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[20].

Закон сохранения механической энергии[править | править код]

Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной^[21].

Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.

Обычно речь идёт о силах инерции двух различных типов^[17][22]. Сила первого типа (даламберова сила инерции^[23]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции^[23]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой

[17]^[22]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются^[24][17], их называют фиктивными^[25], кажущимися^[26] или псевдосилами^[27].

Законы Ньютона в логике курса механики[править | править код]

Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.

Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем

[28].

Страница «Начал» Ньютона с аксиомами механики

Основные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»^[1]:

Оригинальный текст (лат.)

   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.

   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.

   LEX III

Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Русский перевод этих формулировок законов см. в предыдущих разделах.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)^[29]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения

(не вполне ясно использованное у Декарта^[29]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).

В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).

1. ↑ ^{1 2 3} Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
2. ↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. —
   М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
3. ↑ Инерция // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — ISBN 5-85270-061-4.
4. ↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
5. ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
6. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
7. ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
8. ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
9. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
10. ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
11. ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. Архивная копия от 17 июня 2013 на Wayback Machine «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
12. ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45—46. — 368 с. — ISBN 5-93972-051-X.
13. ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
14. ↑ Жирнов Н. И. Классическая механика. — Серия: учебное пособие для студентов физико-математических факультетов педагогических институтов. — М., Просвещение, 1980. — Тираж 28 000 экз. — с. 38
15. ↑ Тютин И. В. Симметрия в физике элементарных частиц. Часть 1. Пространственно-временные симметрии. // Соросовский образовательный журнал, 1996, № 5, с. 65
16. ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 85
17. ↑ ^{1 2 3 4} Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
18. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
19. ↑ Кычкин И. С., Сивцев В. И. Школьная физика: третий закон Ньютона // Международный журнал экспериментального образования. — 2016. — № 3-2. — С. 191—193.
20. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
21. ↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
22. ↑ ^{1 2} Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
23. ↑ ^{1 2} Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3—8.
24. ↑ «„Силы инерции“ — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
25. ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
26. ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
27. ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
28. ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186—197;
29. ↑ ^{1 2} Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160—161, 169—170, 177;

• Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
• Спасский Б. И.. История физики. М., «Высшая школа», 1977.
• Том 1. Часть 1-я; Часть 2-я
• Том 2. Часть 1-я; Часть 2-я
• Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
• Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
• Feynman, R. P. (англ.)русск.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics (неопр.). — 2nd. — Pearson/Addison-Wesley, 2005. — Т. Vol. 1. — ISBN 0-8053-9049-9.
• Fowles, G. R.; Cassiday, G. L. Analytical Mechanics (неопр.). — 6th. — Saunders College Publishing (англ.)русск., 1999. — ISBN 0-03-022317-2.
• Likins, Peter W. (англ.)русск.. Elements of Engineering Mechanics (неопр.). — McGraw-Hill Education, 1973. — ISBN 0-07-037852-5.
• Marion; Jerry; Thornton, Stephen. Classical Dynamics of Particles and Systems (англ.). — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
• NMJ Woodhouse. Special Relativity (неопр.). — London/Berlin: Springer, 2003. — С. 6. — ISBN 1-85233-426-6.
• Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
• Newton, Isaac, «Mathematical Principles of Natural Philosophy», 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
• Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.

Третий закон Ньютона — Википедия

Третий закон Ньютона или закон равенства действия и противодействия — один из трёх основных законов ньютоновской механики.

Закон был впервые сформулирован И. Ньютоном в книге «Математические начала натуральной философии» (1687):

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны^[1].

Более точно, под телами нужно понимать материальные точки; современная формулировка закона такова:

Силы взаимодействия двух материальных точек равны по величине, противоположно направлены, и действуют вдоль прямой, соединяющей эти материальные точки^[2].

В виде формулы:

F→12=−F→21{\displaystyle {\vec {F}}_{12}=-{\vec {F}}_{21}},

где F→12{\displaystyle {\vec {F}}_{12}} — сила, с которой первое тело действует на второе («действие»), а F→21{\displaystyle {\vec {F}}_{21}} — сила, с которой второе тело действует на первое («противодействие»).

• Кирпич, неподвижно лежащий на столе, давит на него с силой P=mg{\displaystyle P=mg}, направленной вниз (и называемой весом). Согласно третьему закону Ньютона, со стороны стола на кирпич действует сила той же величины, направленная вверх (она называется реакцией опоры).
• Яблоко падает на землю, поскольку Земля притягивает его с силой F=mg{\displaystyle F=mg}. При этом, с точно такой же по величине силой яблоко притягивает Землю. Однако, поскольку масса Земли чрезвычайно велика, её перемещение под действием этой силы пренебрежимо мало.

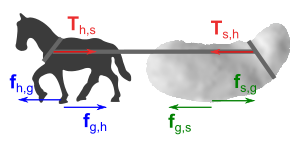
Краткая формулировка закона в виде «действие равно противодействию» может вызывать недоразумения, например такой парадокс:

Пусть лошадь запряжена в телегу, и тянет её с некоторой силой вперёд. Но согласно 3-му закону Ньютона, существует сила противодействия, равная ей по величине и направленная назад. Поскольку в сумме обе силы дают ноль, телега никогда не сможет сдвинуться с места.

Ошибка здесь в том, что силы действия и противодействия приложены к разным телам (в этом примере: к телеге и к лошади), поэтому их бессмысленно складывать. Кроме этих сил, и на лошадь и на телегу действует сила трения, которая, собственно, и приводит лошадь в движение (именно, сила трения копыт лошади об землю направлена вперёд и преодолевает силу противодействия телеги, в то время как сила тяги лошади преодолевает силу трения телеги об землю, направленную назад)^[3].

Рассмотрим два тела, которые взаимодействуют только друг с другом (замкнутая система). Тогда, согласно второму закону Ньютона, их ускорения a→1{\displaystyle {\vec {a}}_{1}} и a→2{\displaystyle {\vec {a}}_{2}} определяются из уравнений

F→21=m1a→1,F→12=m2a→2.{\displaystyle {\vec {F}}_{21}=m_{1}{\vec {a}}_{1},\quad {\vec {F}}_{12}=m_{2}{\vec {a}}_{2}.}

С учётом третьего закона Ньютона отсюда получается

m1a→1+m2a→2=0,{\displaystyle m_{1}{\vec {a}}_{1}+m_{2}{\vec {a}}_{2}=0,}

или же

ddt(m1v→1+m2v→2)=0,{\displaystyle {\frac {d}{dt}}(m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2})=0,}

m1v→1+m2v→2=const,{\displaystyle m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2}={\text{const}},}

где v→1{\displaystyle {\vec {v}}_{1}} и v→2{\displaystyle {\vec {v}}_{2}} — скорости тел. Величина p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} называется импульсом тела, а последнее соотношение есть закон сохранения импульса. Дополнив 3-й закон Ньютона принципом независимости действия сил, можно вывести закон сохранения импульса для замкнутой системы, состоящей из произвольного числа тел. Хотя в рамках ньютоновской механики закон сохранения импульса является следствием законов Ньютона, опыт показывает, что это один из наиболее общих законов физики, который выполняется даже тогда, когда сама ньютоновская механика неприменима^[2].

Как 3-й закон Ньютона, так и более общий закон сохранения импульса являются следствиями фундаментальной симметрии природы — однородности пространства. Однородность пространства означает, что все его точки равноправны, то есть, закон движения замкнутой системы не изменится, если систему переместить в пространстве как целое.

Связь 3-го закона Ньютона с однородностью пространства хорошо видна в рамках лагранжева формализма. Если пространство однородно, то потенциальная энергия может зависеть только от разностей координат тел: U=U(r→1−r→2){\displaystyle U=U({\vec {r}}_{1}-{\vec {r}}_{2})}, поэтому

F→21=−dUdr→1=−∇→U(r→1−r→2),{\displaystyle {\vec {F}}_{21}=-{\frac {dU}{d{\vec {r}}_{1}}}=-{\vec {\nabla }}U({\vec {r}}_{1}-{\vec {r}}_{2}),}

F→12=−dUdr→2=∇→U(r→1−r→2),{\displaystyle {\vec {F}}_{12}=-{\frac {dU}{d{\vec {r}}_{2}}}={\vec {\nabla }}U({\vec {r}}_{1}-{\vec {r}}_{2}),}

откуда следует F→21=−F→12{\displaystyle {\vec {F}}_{21}=-{\vec {F}}_{12}}^[4].

Третий закон Ньютона, как и вообще вся ньютоновская механика, связан с идеей действия на расстоянии, согласно которой сила, действующая со стороны одного тела на другое в некоторый момент времени, определяется их положением в тот же момент времени. Другими словами, это означает бесконечную скорость передачи взаимодействий. Согласно современным представлениям, взаимодействия передаются посредством полей, и, как следует из опыта, имеют конечную скорость, не превышающую скорости света. Поэтому при движении со скоростями, близкими к скорости света, или же когда расстояния между телами слишком велики, третий закон Ньютона неприменим. Однако закон сохранения импульса по-прежнему выполняется, если кроме импульса тел, учесть также импульс поля (например электромагнитного, гравитационного), посредством которого они взаимодействуют^[2].

Пример: на тело, поглощающее свет, действует сила давления света. Но никакой «силы противодействия» здесь нет, как нет и никакого тела, к которому она была бы приложена. С точки зрения закона сохранения импульса, давление света возникает потому, что импульс электромагнитного поля передаётся телу^[2].

Силы, законы Ньютона — базовый урок по физике

А вот в неинерциальных системах скорость тела может меняться без силы.

Например: представьте, что вы стоите в центре автобуса, равномерно едущего по ровной дороге. Находясь внутри, вы даже не чувствуете, что автобус едет. В какой-то момент автобус резко тормозит и вас «бросает» вперед, хотя не действует никакая сила. То есть вы начинаете двигаться относительно автобуса без всякой причины. В таком случае автобус — это пример неинерциальной системы отсчета.

Неинерциальные системы отсчета — это системы, которые двигаются с ускорением. В таких системах вводятся так называемые силы инерции, чтобы при расчетах также можно было пользоваться законами Ньютона.

Нашу Землю можно условно отнести к инерциальным системам отсчета, поскольку вращение Земли есть ни что иное, как движение с центростремительным ускорением. Но так как Земля вращается достаточно медленно, то и центростремительное ускорение получается небольшим.

С высокой степенью точности инерциальной является гелиоцентрическая система отсчета (или система Коперника), начало которой помещено в центр Солнца, а оси направлены на далекие звезды. Вообще всякая система отсчета, движущаяся относительно какой-либо инерциальной системы поступательно, равномерно и прямолинейно, также является инерциальной. Например, поезд, идущий с постоянной скоростью по прямому участку пути.

Первый закон постулирует существование инерциальных систем отсчета, но не говорит, какую из множества таких систем предпочтительней выбирать. Однако многочисленные опыты показывают, что все инерциальные системы отсчета являются равноправными.

Когда мы говорим о скорости какого-либо тела, мы обязательно должны указать, относительно какой инерциальной системы отсчета она измерена, так как в разных инерциальных системах эта скорость будет различна, хотя бы на тело и не действовали никакие другие тела. Ускорение же тела будет одним и тем же относительно всех инерциальных систем отсчета.

5.4. Закон действия и противодействия. Секреты мироздания

5.4. Закон действия и противодействия

Существует три типа действий: хорошие, то есть чистые действия, приносящие счастье; грешные действия, приносящие страдания, и нейтральные. Действия никогда не проходят бесследно. «Каждому действию есть равное и противоположно направленное противодействие» — гласит третий закон Ньютона. Закон этот всеобщий и приложим не только к материи, но и к сознанию (то есть к духовной сфере). Он действует независимо от наших желаний. Никто никогда не может избежать результатов того, что совершил. Каждому придется пожинать плоды своих действий, если не сразу, то спустя какое-то время или даже в последующих рождениях. Каковы действия — таковы и плоды. Не случайно говорится: «Что посеешь, то и пожнешь».

Если я причинил кому-то страдание, то обязательно получу плод (счет) — страдание, а если подарил счастье, то плодом этого будет счастье.

Счастье и страдание — это счета наших собственных действий. Однако, как правило, мы наблюдаем за плодами, отстоящими довольно далеко по времени от породивших их действий.

Поэтому и не осознаем своей собственной ответственности за полученный плод. В таких случаях мы зачастую указываем пальцем на других, говоря, что это они виновны в наших страданиях и неудачах. А некоторые даже считают, что это Бог контролирует страдание и счастье. Счета за действия — это счета лично каждого.

Какие бы действия ни совершал кто-либо, он обязательно накапливает их счета и рано или поздно непременно получает возврат своих действий — хороших или плохих. Например, если кто-то рождается в королевской семье, то это не какая-то случайность, а плод огромной благотворительности, совершенной данной душой в предыдущем рождении. Когда человек на свои средства открывает колледж, то он получает большую мудрость в следующем рождении. Если у кого-то развилась привычка воровать, то он примет рождение в неблагополучной семье. Именно от наших поступков в предыдущем рождении зависит то, в какой семье мы рождаемся — в хорошей или плохой. Все это — счета за совершенные действия. Болезни — тоже счета за грешные действия, совершенные если не в этом, то в прошлых рождениях.

Когда человек гневается, то он приносит боль не только другим, но в первую очередь самому себе. Его мучает совесть, появляется напряжение ума, портится настроение и т. д. Такое стрессовое состояние ведет к нарушению деятельности сердечно-сосудистой системы, к выделению рядом желез вредных веществ, которые, попадая в кровь, наносят вред здоровью.

Итак, причина наших сегодняшних страданий — грешные действия, которые были совершены нами в этой жизни, или же мы расплачиваемся за содеянное нами в предыдущих рождениях.

Закон действия и противодействия накладывает на человека полную ответственность за его собственную судьбу. Понимание этого закона делает нас не рабами, а творцами своей судьбы. Совершая хорошие, чистые действия сейчас, каждый может создать свое будущее по собственному выбору.

Поделитесь на страничке

Следующая глава >

Действие и противодействие. — О пользе бесполезного — ЖЖ

      Есть одна очень важная, очень философская, я бы сказал, очень даосская, тема — деятельность. В принципе, действия совершают и животные, даже простые двигательные акты, такие как ходьба, могут быть расценены как действия.  Но человек не просто действует — его действия превращаются в деятельность. То есть многие мысли, движения определяются некоей целью, планом, идеей, ведут к чему-то заданному самим человеком. Ключевой момент для деятельности — намерения. Целесообразны могут быть и естественные действия, но деятельность складывается из намеренных действий. Именно о таких действиях, из которых состоит почти вся жизнь современного человека, и человечества в целом, я и хотел поговорить. Конечно, намерение не входит в само действие, оставаясь в сфере мотивации и стимуляции, но без рассмотрения намерений любой разговор о действиях неполноценен.  Почему-то никто не спешит называть убийцей того, кто уронил кирпич, который упал и убил человека — хотя ясно, что именно действие уронившего кирпич привело к трагедии. Можно говорить о халатности, случайности, возлагать ответственность — но действие здесь будет рассматриваться не как элемент деятельности. Точно так же не деятельность непроизвольный зевок. 
       Что же можно включить в деятельность? Намеренную активность, не исключая и произнесение слов, что тоже является видом действия. Чем больше целенаправленности, ориентации на результат — тем с большим правом действие вписывается в деятельность. В истории находились люди, которые ощущали опасность деятельности, в частности представления об этом отражены в буддизме и отчасти в христианстве. Что такое «суета сует»? Безусловно, это не только бесполезность действий, но и некая бессмысленность, уводящая от подлинной жизни. Но только ранние даосские мыслители прямо сказали об опасности деятельности. Мало кто понял их слова два тысячелетия назад, но и сейчас люди так же глухи к этим истинам…   Деятельность плоха не тем, что человек в итоге страдает, а тем что нарушается миропорядок. Необязательно досконально знать биологию и экологию, можно и интуитивно чувствовать нарушение естественного хода вещей. Человек издавна разрушает и уничтожает природу, в том числе подавляя её в себе же самом. Деятельность вылилась в создание цивилизации и технический прогресс. Теперь уже не человек направляет деятельность, но она направляет его. Упрощая, можно себе это представить как некую инерцию — сначала действие совершается намеренно, а потом идет по инерции, а последствия этого действия сказываются уже независимо от наших желаний. Самое опасное — не думать и не предвидеть последствий деятельнсоти. И чем масштабнее и тоньше деятельность — тем сложнее предвидеть последствия и управлять действиями. Американская экологическая катастрофа с нефтяной вышкой — хорошее тому подтверждение. Не построили бы вышку — ничего бы не случилось. Означает ли это, что следует полностью отказаться от деятельности?  А почему, бы, собственно, и не отказаться?
      В легендах об утерянном рае есть одна очень глубокая правда — раньше человек жил дарами — природы, конечно, которая в некоторых учениях выступает слепым орудием бога, но это несущественно. Со временем человек стал не добывать пищу и прочее, а создавать их. Началась эра деятельности, эра человеческого дао. Любая активность стала деятельностью.  Мы обычно мысленно противопоставляем действие и противодействие, что совершенно неверно. Представьте, что вы бьете по резиновому мячу и ваша рука отскакивает. разве мяч противодействует? Вовсе нет, это последствие вашего действия, продолжение его. Между прочим, некоторые мистифицируют ситуацию и говорят о некоем ответе природы, о наказании человека. А ведь мы всего лишь пожинаем то, что сеем, не более того. Противодействие есть действие. Только направление его обратное. Чаще всего люди, когда сталкиваются с чем-то неприемлемым для них, начинают действовать. Своё действие они подают как бунт, протест, движение за освобождение. На самом деле они заменяют одну кабалу другой, меняют одно действие на другое. Ничего существенного такой заменой не достичь. Более того, во многих случаях противодействие усиливает действие, подливает масла в огонь. Ответом на действие, реакцией на нежелательную деятельность должны быть не противодействие и не равнодушие, а уклонение. Говоря иначе — активное неучастие. Делая нечто другое, делая иначе, делая естественно, мы можем избежать расставленной ловушки. Это как клей — против него бесполезно применять силу. Муха в паутине запутывается тем сильнее, чем больше старается выбраться.
       Чтобы избежать ошибок, следуят уяснить, что противодействие не нейтрализует действие. При столкновении действия и противодействия последствия могут быть гораздо худшими, чем если противодействие будет отсутствовать. К опасности деятельности добавляется опасность оппозиционности. С Системой, с государством, с любым глобальным злом неразумно бороться деятельно. Мнимо отказываяь от чего-то, на самом деле мы остаемся ему причастны. Осавобождение от плена деятельности есть не какая-то буддийская неподвижность и созерцательность, а естественная активность с отказом от намеренности. Разум опасен не сам по себе, цивилизация опасна не сама по себе. Любое зло воплощается в деятельности, любая деятельность влечет губительные последствия, даже если сразу это незаметно. Спонтанность жизни есть огромная — и пока мало кем признанная ценность. До тех пор пока опасность деятельности и ценность естественности не будет осознана — никакие противодействия явным угрозам (к примеру, борьба за мир или экологическое движение)  не принесут желаемых результатов. 

Действия и противодействия закон — это… Что такое Действия и противодействия закон?



Действия и противодействия закон

        один из основных законов механики (третий закон Ньютона), согласно которому действия двух материальных тел друг на друга равны по численной величине и противоположны по направлению. Например, сила, с которой груз, лежащий на плоскости, давит на эту плоскость, равна силе (реакции), с которой плоскость давит на груз; сила, с которой Земля притягивает Луну, равна силе, с которой Луна притягивает Землю, и т.д. Следует иметь в виду, что названные силы действия и противодействия не уравновешивают друг друга, т.к. они приложены к разным телам. Д. и п. з. играет важную роль при изучении движения механических систем (см. Динамика).

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Действительный студент
• Действующая длина

Смотреть что такое «Действия и противодействия закон» в других словарях:

• ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН — один из осн. законов механики (третий закон Ньютона), согласно к рому действия двух матер. тел друг на друга равны по величине и противоположны по направлению. Напр., сила, с к рой груз, лежащий на плоскости, давит на эту плоскость, равна силе… …   Физическая энциклопедия

• ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН — (третий закон механики Ньютона) см. Ньютона законы …   Большой Энциклопедический словарь

• ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН — третий из осн. законов механики (см. Ньютона законы механики). Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 …   Физическая энциклопедия

• действия и противодействия закон — (третий закон механики Ньютона), см. Ньютона законы. * * * ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН (третий закон механики Ньютона), см. Ньютона законы (см. НЬЮТОНА ЗАКОНЫ) …   Энциклопедический словарь

• ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ ЗАКОН — (третий закон механики Ньютона), см. Ньютона законы …   Естествознание. Энциклопедический словарь

• ЗАКОН ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ — см …   Большая политехническая энциклопедия

• закон действия и противодействия — veiksmo ir atoveiksmio dėsnis statusas T sritis fizika atitikmenys: angl. law of action and reaction vok. Gegenwirkungsprinzip, n; Gesetz von der Wirkung und Gegenwirkung, n rus. закон действия и противодействия, m pranc. principe d’action et de… …   Fizikos terminų žodynas

• Закон Сарбейнза — Оксли — 30 июля 2002 г. Президент Буш подписал Закон Сарбейнза Оксли (англ. Sarbanes Oxley Act), который представляет собой одно из самых значительных событий по изменению федерального законодательства США по ценным бумагам за последние 60 лет.… …   Википедия

• Закон Сарбейнза — 30 июля 2002 г. Президент Буш подписал Закон Сарбейнза  Оксли (англ. Sarbanes Oxley Act, SOX), который представляет собой одно из самых значительных событий по изменению федерального законодательства США по ценным бумагам за… …   Википедия

• Закон Сарбанеса — Оксли — 30 июля 2002 г. Президент Буш подписал Закон Сарбейнза Оксли (англ. Sarbanes Oxley Act), который представляет собой одно из самых значительных событий по изменению федерального законодательства США по ценным бумагам за последние 60 лет.… …   Википедия

Законы Ньютона — это… Что такое Законы Ньютона?

Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год).

Первый закон Ньютона

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[1]:

Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Историческая формулировка

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где  — ускорение материальной точки;
 — сила, приложенная к материальной точке;
 — масса материальной точки.

Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где  — импульс точки,

где  — скорость точки;

 — время;
 — производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

или

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[2].

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел , то возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.

Комментарии к законам Ньютона

Сила инерции

Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона: , где — это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и — ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции» , и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета.

Законы Ньютона и Лагранжева механика

Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Решение уравнений движения

Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Исторический очерк

Страница «Начал» Ньютона с аксиомами механики

Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.    2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.    3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Оригинальный текст  (лат.)      LEX I Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.    LEX II Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.    LEX III Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi. — «Начала», страница 12

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).

Завершили математизацию механики Эйлер и Лагранж.

См. также

Примечания

Ссылки

Литература