Как сделать пластина хладни: Фигуры Хладни: что это такое. Фигуры Хладни в домашних условиях: как сделать

Фигуры Хладни: что это такое. Фигуры Хладни в домашних условиях: как сделать

Содержание

Эксперимент Хладни
Фигуры Хладни в домашних условиях

О влиянии звука на тело и сознание человека сегодня уже слышали многие. Даже существует мнение, что западная низкочастотная музыка специально была создана для того, чтобы воздействовать на тело и сознание человека. И поведение людей на концертах такой музыки говорит само за себя – отмечается возбуждение нервной системы, раздражённость, агрессивность и так далее. Именно так воздействуют на человека низкие частоты, чего нельзя сказать о классической музыке, в которой преобладают высокочастотные звуки. И такая музыка исцеляюще воздействует на человека.

Звук – своего рода живая энергия, которую можно не только услышать, но и… увидеть. Да, именно так. Благодаря изобретению одного талантливого учёного это стало возможным.

Немецкий учёный, Хладни Эрнст Флоренс Фридрих ещё в 18-ом веке изобрёл способ, благодаря которому звук можно увидеть.

Надо сказать, что немецкий физик не был первооткрывателем в этой области. Впервые особенность звука оказывать воздействие на окружающие предметы отметил английский учёный Роберт Гук ещё в 1680-ом году. Его исследования, которые он проводил в Оксфордском университете, показали, что предметы способны менять свою форму под воздействием колебаний.

Как именно это произошло? Роберт Гук отметил, что если воздействовать смычком на край металлической пластины, которая покрыта мукой, то мука начинает движение и постепенно формирует узоры.

Немецкий физик Эрнст Хладни продолжил работать в этом направлении. По мере того, как он накопил определённый опыт в этой сфере, он издал книгу «Теория Звука», в которой подробно описал свои эксперименты.

В чём же важность и ценность проведённых Эрнстом Хладни исследований? Во-первых, как говорил сам Хладни, благодаря его исследованию появилась возможность «звук не только слышать, но и видеть».

Во-вторых, он эмпирическим путём доказал существование стоячей звуковой волны, которая собственно и формирует все эти диковинные узоры. Но самое главное, эксперимент Эрнста Хладни наглядно показывает, как сильно отличаются низкие и высокие звуковые вибрации.

Суть эксперимента в том, что при низких вибрациях формируются самые грубые простые узоры – геометрические фигуры: квадраты, кресты, круги и иже с ними. Но по мере повышения вибрации звука происходит настоящее чудо: на пластинах вырисовываются всё более сложные узоры – звёзды, орнаменты и так далее.

И это яркий пример того, как разные звуковые вибрации могут воздействовать на окружающий мир. И значит, воздействие звука на человека – это вовсе не миф. Ведь если под действием вибраций песок перемещается по пластине, образуя те или иные узоры, значит, некие процессы также проходят и на клеточном уровне в теле человека – клетки также реагируют на те или иные вибрации. И совершенно очевидно, что низкие и высокие вибрации действуют на человека не одинаково.

Именно этим объясняется такая разница ощущений на концерте рок-музыки и на концерте классической музыки.

Всё это может показаться какой-то фантастикой. Но главное преимущество науки в том, что любой желающий может повторить тот или иной эксперимент и убедиться в том, что это не миф, а реально существующий факт. Эксперимент с фигурами Хладни можно повторить в домашних условиях. Что нам для этого потребуется?

Как сделать фигуры Хладни в домашних условиях? Для этого нам потребуется металлическая пластина, закреплённая по центру, а также скрипичный смычок. Скрипичный смычок в данном случае будет наиболее удобным, но может подойти альтовый, виолончельный и контрабасовый. Также нам потребуется некий мелкодисперсный порошок, в классическом варианте используется песок, но проще будет использовать то, что найдётся на кухне – манную крупу, соль или соду. Сахар, скорее всего, не подойдёт, так как имеет слишком крупные кристаллы.

Для проведения эксперимента нам необходимо будет насыпать на поверхность пластины песок, манку или соль, а затем проводить по торцу пластины смычком. Пластина будет издавать звуковые вибрации, и на наших глазах под воздействием этих вибраций будет формироваться рисунок.

Важно отметить, что пластины квадратной формы при воздействии смычка будут издавать низкие вибрации, а вот пластины круглой формы – более высокие. Поэтому, если есть желание и возможность увидеть именно разницу между низкими и высокими вибрациями, необходимо повторить эксперимент на квадратной и на круглой пластине. Звук, издаваемый квадратной пластиной, будет формировать более примитивные узоры, а звуки на круглой пластине – более замысловатые.

В классическом варианте в лабораторных условиях уже не используется смычок, как это делал сам Эрнст Хладни. С начала 20-го века для эксперимента с фигурами Хладни стали использовать громкоговоритель с генератором звука под самой пластиной. Это позволяет механизировать процесс, а самое главное – чётко регулировать частоты воспроизводимого звука и наблюдать за переменами в рисунке при минимальных изменениях в воспроизводимых частотах.

Эксперимент Хладни даёт ответы на вопросы

Помимо того, что фигуры Хладни наглядно демонстрируют тот факт, что звук способен влиять на окружающий мир и в том числе на человека, это открытие позволяет по-новому взглянуть на археологические находки. Учёные много лет ищут ответ на вопрос: как древним людям, которые согласно официальной исторической версии были дикарями и кроме каменного топора сделать ничего не могли, всё же удавалось строить такие удивительные сооружения. Примерами могут быть гробницы, древние храмы и так далее.

Эксперимент Хладни приоткрывает завесу тайны в этом вопросе. Не исключено, что уже задолго до открытия немецкого физика наши предки знали о чудодейственных

способностях звука и его возможности воздействовать на материю. Возможно, они нашли способ с помощью звуковых вибраций гравировать те сложные рисунки, которые часто вводят в недоумение археологов. В самом деле, уж явно не с помощью пресловутого каменного топора или «палки-копалки» были сделаны эти диковинные узоры. И эксперимент Хладни позволяет задуматься о том, что, возможно, наши предки были гораздо более развитыми, чем мы привыкли думать.

Ну и самое главное, эксперимент Хладни позволяет увидеть, что низкие и высокие звуковые вибрации действуют на материю по-разному. И это ещё раз доказывает, что низко-вибрационная музыка, которая сейчас как раз таки наиболее популярна, огрубляющим образом воздействует как на материю, так, очевидно, и на сознание. А музыка с высокими вибрациями, способная создавать сложные узоры, скорее всего, на тело и сознание действует исцеляющим образом.

Фигуры Хладни и квантовый хаос / Хабр

Насыпав песок на колеблющуюся упругую пластинку, можно увидеть формирование фигур Хладни. Они часто служат примером «естественной красоты» физических явлений, хотя за ними стоит довольно простая физика резонансного возбуждения стоячих волн. И мало кто обращает внимание на любопытную особенность этих фигур: линии на них избегают пересечений, будто их отталкивает некая сила.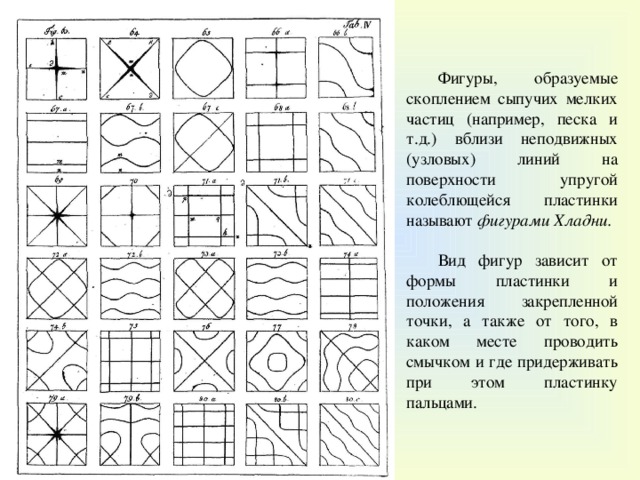

Давайте попробуем понять, какая же физика скрывается за этим отталкиванием и как она связана с квантовой теорией хаоса.

Как мы знаем, упругие тела могут совершать довольно сложные колебания, при которых они сжимаются, растягиваются, изгибаются и скручиваются. Тем не менее, колебания любого упругого тела можно представить как комбинацию накладывающихся друг на друга более простых нормальных колебаний. Вот так выглядят несколько нормальных колебаний простейшего упругого тела – одномерной натянутой струны.

Каждое нормальное колебание представляется стоячей волной, которая, в отличие от бегущей волны, стоит на месте и обладает своим рисунком распределения амплитуд колебаний по пространству. На этом рисунке можно выделить пучности – точки, где амплитуда колебаний достигает максимумов, и узлы – неподвижные точки, в которых амплитуда колебаний равна нулю. Кроме того, каждая такая волна колеблется со своей

собственной частотой.

В случае струны, как можно заметить, частота колебаний стоячей волны увеличивается с ростом числа узлов и пучностей.

Посмотрим теперь на двумерную систему, примером которой может служить тонкая упругая мембрана, натянутая на жесткую рамку. Нормальные колебания круглой мембраны выглядят сложнее, чем в случае струны, а вместо отдельных точек-узлов имеются узловые линии, вдоль которых мембрана неподвижна.

Нормальные колебания круглой мембраны с закрепленными краями. Источник.

Зеленым цветом показаны узловые линии.

У круглой мембраны узловые линии, представляющие собой окружности и отрезки вдоль радиусов, могут пересекаться под прямыми углами. Если же края мембраны имеют произвольную форму, нахождение частот нормальных колебаний и картин их узлов и пучностей превращаются в задачу, решаемую только с помощью компьютера.

Профили амплитуды колебаний стоячих волн на мембранах в форме квадрата с отверстием, снежинки Коха и поверхности котенка.

Уравнения, описывающие колебания тонкой упругой пластинки, отличаются от уравнений колебания мембраны, поскольку пластинка обладает собственной жесткостью, в то время как мембрана мягкая и пружинит лишь за счет натяжения внешними силами. Однако здесь тоже существуют наборы нормальных колебаний, рисунки которых существенным образом зависят от формы границ.

Как было сказано выше, в общем случае колебания тела представляют собой комбинацию целого набора возбужденных в нем нормальных колебаний. Явление резонанса позволяет выборочно возбудить какое-то одно нужное нам нормальное колебание – для этого следует раскачивать тело при помощи внешней силы с частотой, равной собственной частоте нормального колебания.

На двух видео ниже показана типичная схема получения фигур Хладни: упругая пластинка прикрепляется в центре к генератору механических колебаний, частоту которых плавно увеличивают. Нормальные колебания пластинки со своими картинами узлов и пучностей возбуждаются при резонансном совпадении частоты генератора с собственными частотами этих колебаний (собственные частоты показаны на видео в левом нижнем углу).

Здесь версия этого же видео, на которой частоты нормальных колебаний можно оценить на слух.

А здесь немного красивее.

Картины узлов и пучностей мы видим благодаря тому, что воздушные потоки вблизи колеблющейся пластинки сдувают песчинки к узловым линиям стоячей волны^(*). Таким образом, фигуры Хладни показывают нам картины узловых линий нормальных колебаний упругой пластинки.

Несколько фигур Хладни на верхней деке гитары. Источник.

Еще пример нормальных волн – это стоячие волны на поверхности воды. Они описываются уравнением, отличающимся от уравнений колебания пластинок и мембран, но следуют таким же качественным закономерностям, и с их помощью можно получать аналоги фигур Хладни.

Микрочастицы на поверхности воды в сосудах разной формы. Черная линия показывает масштаб 2 миллиметра. Источник.

Итак, мы видели, что в случае круглой мембраны узловые линии – теоретически! – замечательно пересекаются, в то же время на фигурах Хладни на квадратных или более сложных пластинках узловые линии избегают пересечений. Чтобы понять причину этих закономерностей, нам придется сделать небольшой экскурс в теорию хаоса.

Классический хаос – это свойство механических систем, заключающееся в чрезвычайно сильной зависимости траектории их движения от изменений начальных условий. Эта зависимость известна также как «эффект бабочки». Яркий пример хаотического поведения можно встретить при попытках предсказания погоды: система уравнений, описывающая движение атмосферы и океанов, не позволяет дать достаточно точные прогнозы на больших временах из-за экспоненциально нарастающих ошибок, обусловленных малыми неточностями исходных данных^(**).

Явление хаоса было открыто и популяризовано метеорологом и математиком Эдвардом Лоренцем, обнаружившим, что два расчета прогноза погоды, начинающиеся с очень близких начальных условий, сначала почти неотличимы друг от друга, но с какого-то момента начинают кардинально расходиться.

Два расчета Эдварда Лоренца, исходящие из близких начальных значений 0.506 и 0.506127. Источник.

Простейшими системами, на примере которых удобно изучать хаос, являются бильярды – участки плоской поверхности, по которым без трения может катиться шарик, абсолютно упруго отскакивающий от жестких стенок. В хаотических бильярдах траектории движения шарика, имеющие незначительные отличия в самом начале, в дальнейшем существенно расходятся. Пример хаотического бильярда – изображенный ниже бильярд Синая, представляющий собой прямоугольный бильярд с круговым препятствием в центре. Как мы увидим, именно за счет этого препятствия бильярд становится хаотическим.

Две экспоненциально расходящиеся траектории шарика в бильярде Синая. Источник.

Механические системы, не являющиеся хаотическими, называются интегрируемыми, и на примере бильярдов можно наглядно увидеть разницу между интегрируемыми и хаотическими системами.

Прямоугольный и круглый бильярды являются интегрируемыми благодаря своей симметричной форме^(***). Движение шарика в таких бильярдах – это просто комбинация двух независимых периодических движений. В прямоугольном бильярде это движения с отскоками от стенок по горизонтали и по вертикали, а круглом это движение вдоль радиуса и угловое движение по окружности вокруг центра. Такое движение легко просчитываемо и не показывает хаотического поведения.

Траектории движения шарика в интегрируемых бильярдах.

Бильярды более сложной формы, не обладающие столь высокой симметрией, как у круга или прямоугольника, являются хаотическими^(****). Один из них мы видели выше – это бильярд Синая, в котором симметрия прямоугольника разрушается круговым включением в центре. Также часто рассматриваются бильярд «стадион» и бильярд в форме улитки Паскаля. Движение шарика в хаотических бильярдах происходит по весьма запутанным траекториям и не раскладывается на более простые периодические движения.

Траектории движения шарика в хаотических бильярдах «стадион» и «улитка Паскаля».

Здесь можно уже догадаться, что наличие пересечений между линиями на фигурах Хладни определяется тем, имеет ли пластинка форму интегрируемого или хаотического бильярда. Это наглядно видно на фотографиях ниже.

Круглые пластинки Хладни, демонстрирующие свойства интегрируемых бильярдов. Источник.

Демонстрирующие свойства хаотических бильярдов пластинки Хладни в форме бильярда «стадион», корпуса скрипки и квадрата, симметрия которого нарушена круглым креплением в центре (аналог бильярда Синая). Источник.

Как же понять, почему наличие пересечений между узловыми линиями обусловлено интегрируемостью бильярда? Для этого нужно обратиться к квантовой теории хаоса, объединяющей теорию хаоса с механикой колебаний и волн. Если в классической механике шарик в бильярде описывается в виде материальной точки, движущейся вдоль определенной траектории, то в квантовой механике его движение описывается как распространение волны, подчиняющейся уравнению Шредингера и отражающейся от стенок бильярда.

Этапы распространения волны в квантовом бильярде. Изначально волна сконцентрирована в импульсе круглой формы и движется слева направо, затем она расплывается и многократно переотражается от стенок. Источник.

То же самое в виде анимации, но с немного другими начальными условиями.

Как и в случае колебаний мембран и пластинок, описывающее квантовый бильярд уравнение Шредингера позволяет найти нормальные колебания в виде стоячих волн, обладающие характерным рисунком узловых линий и пучностей, индивидуальным для каждого колебания и зависящим от формы границ.

Примеры профилей амплитуд колебаний в стоячих волнах в хаотических квантовых бильярдах «улитка Паскаля» и «стадион».

Рисунки стоячих волн в интегрируемых и хаотических квантовых бильярдах качественно отличаются: интегрируемые бильярды показывают симметричные, упорядоченные картины стоячих волн, в то время как в хаотических бильярдах рисунки стоячих волн весьма запутанные и не показывают никаких видимых закономерностей (в конце статьи будет показано, что некоторые интересные закономерности там все-таки существуют).

Амплитуды колебаний в стоячих волнах интегрируемого круглого бильярда (верхний ряд) и хаотического бильярда в форме улитки Паскаля (нижний ряд). Источник.

Причудливые картины нормальных колебаний в хаотических бильярдах иногда служат предметом отдельного исследования. Источник.

Качественное отличие видно и в картинах узловых линий: в случае интегрируемого квантового бильярда мы видим упорядоченные семейства взаимно пересекающихся линий, а в хаотических бильярдах эти линии, как правило, не пересекаются.

Вверху: узловые линии (черные линии между синими и красными областями) стоячих волн интегрируемых – круглого и прямоугольного – бильярдов. Внизу: узловые линии одной из стоячих волн в хаотическом бильярде – четверти бильярда «стадион».

Почему же узловые линии в хаотических бильярдах не пересекаются? В 1976 году математик Карен Уленбек доказала теорему, согласно которой узловые линии стоячих волн квантовых бильярдов, вообще говоря, и не должны пересекаться.

В упрощенном виде это можно показать следующим образом: допустим, что две узловые линии пересекаются в точке (x₀,y₀). Чтобы такое произошло, функция f(x,y), задающая зависимость амплитуды стоячей волны от координат, должна одновременно удовлетворять трем условиям:

1) Она должна быть равна нулю в точке (x₀,y₀), так как эта точка является узловой.
2) Если двигаться из точки (x₀,y₀) в направлении первой узловой линии, то f(x,y) должна оставаться равной нулю.
3) Если двигаться из точки (x₀,y₀) в направлении второй узловой линии, то f(x,y) также должна оставаться равной нулю.

Итого имеем три условия (или три уравнения), наложенные на функцию двух переменных f(x,y). Как мы знаем, одного уравнения недостаточно для полного нахождения двух неизвестных x и y, двух уравнений для этого уже достаточно, а три уравнения – это слишком много. Система трех уравнений для двух неизвестных, вообще говоря, решений иметь не будет, если только нам случайно не повезет. Поэтому точки пересечения узловых линий могут существовать только в порядке исключения.

В интегрируемых бильярдах такие исключения как раз и возникают. Как мы видели выше, их особые свойства – предсказуемость движения, отсутствие хаоса, регулярные рисунки стоячих волн – являются следствием их высокой симметрии. Эта же симметрия обеспечивает и одновременное выполнение трех условий, необходимое для пересечений узловых линий.

Давайте теперь более внимательно посмотрим на примеры фигур Хладни, типичных для интегрируемых и хаотических бильярдов. На рисунке ниже показаны три характерных случая. Слева пластинка имеет форму круга, поэтому соответствующий квантовый бильярд является интегрируемым, и узловые линии пересекаются между собой. В центре пластинка прямоугольная, что тоже соответствует интегрируемой системе, однако круглое крепление в центре слегка нарушает симметрию прямоугольника, поэтому узловые линии пересекаются не везде. Справа показан пример чисто хаотической системы: пластинка в форме четверти бильярда Синая (в верхнем правом углу есть круговой вырез), узловые линии на которой уже не пересекаются.

Таким образом, чем сильнее форма пластинки – с учетом ее крепления – отличается от формы интегрируемого бильярда (такого как круг или прямоугольник), тем меньше на ней пересечений узловых линий.

Получить красивые фигуры Хладни с пересекающимися линиями на круглой пластинке не так-то просто. При возбуждении колебаний с центральным креплением круговая симметрия всей системы запрещает формирование радиальных узловых линий, поэтому мы увидим лишь скучный набор окружностей (эту трудность можно обойти, возбуждая колебания не с центра, а с края пластинки при помощи смычка от скрипки). Если же пластинку закрепить не по центру, фигуры Хладни станут интереснее, но из-за нарушения круговой симметрии система перестанет быть интегрируемой.

Круглая пластинка, крепление по центру.

Круглая пластинка, крепление сдвинуто из центра.

А здесь разные варианты с круглыми и некруглыми пластинками.

Наконец, внимательный читатель может заметить: а я вижу, что иногда узловые линии пересекаются даже на «хаотических» пластинках. Как же так, если их пересечение запрещено теоремой Уленбек?

Во-первых, узловые линии могут избегать пересечения, но перед этим сближаться так сильно, что из-за конечной ширины дорожки песка нам будет казаться, что пересечение есть. Во-вторых, между интегрируемыми и хаотическими системами на самом деле не существует резкой границы.

Узловые линии – они разделяют черные и белые области – в интегрируемом и хаотическом квантовых бильярдах (слева и справа), и в промежуточном псевдоинтегрируемом случае (в центре). В промежуточном случае есть несколько пересечений узловых линий, в то время как в хаотическом случае их нет вовсе. Источник.

В классической теории хаоса этому вопросу посвящена знаменитая теория Колмогорова-Арнольда-Мозера. Она говорит о том, что если слегка нарушить симметрию интегрируемой системы, то она не станет сразу же проявлять хаотическое поведение, а, по большей части, сохранит свое свойство предсказуемости движения. На уровне квантовой теории хаоса и фигур Хладни это проявляется в том, что в некоторых местах пересечения узловых линий сохраняются. Это происходит либо в особо симметричных точках бильярда, либо далеко от источника возмущения, нарушающего симметрию интегрируемой системы.

Чем еще интересна квантовая теория хаоса? Для заинтересованного читателя упомяну о трех дополнительных вопросах, уже не связанных непосредственно с фигурами Хладни.

1) Важное явление, изучаемое этой теорией – универсальность хаотических систем. Подавляющее большинство систем, в которых могут возникать нормальные колебания, являются хаотическими, и все они – независимо от своей физической природы! – подчиняются одинаковым закономерностям. Феномен универсальности, при котором совершенно разные системы описываются одними и теми же формулами, сам по себе очень красив и служит нам напоминанием о математическом единстве физического мира.

Статистика расстояний между соседними частотами нормальных колебаний в хаотических системах разной физической природы, везде описываемая одной и той же универсальной формулой Вигнера-Дайсона. Источник.

2) Рисунки нормальных колебаний хаотических бильярдов обладают интересной особенностью, называемой «квантовыми шрамами». Мы видели, что траектории движения шарика в хаотическом бильярде обычно выглядит весьма запутанными. Но есть и исключения – это периодические орбиты, достаточно простые и короткие замкнутые траектории, вдоль которых шарик совершает периодическое движение. Квантовыми шрамами называются резкие сгущения стоячих волн вдоль периодических орбит.

Квантовые шрамы в бильярде «стадион», идущие вдоль периодических орбит, показанных красными и зелеными линиями. Источник.

3) До сих пор мы говорили о двумерных системах. Если же рассматривать распространение волн в трехмерном пространстве, то здесь тоже могут возникать узловые линии, вдоль которых амплитуда колебаний равна нулю. Особенно важно это при изучении бозе-конденсации и сверхтекучести, где тысячи атомов движутся как единые «волны материи». Анализ структуры узловых линий волн материи в трехмерном пространстве необходим, например, для понимания того, как возникает и развивается квантовая турбулентность в сверхтекучих системах.

Запутанные трехмерные структуры узловых линий стоячих «волн материи» в бозе-конденсате. Источник.

^(*) Если размер частичек, насыпанных на пластинку, достаточно мал, то их будет сдувать уже не к узлам, а к пучностям стоячей волны, как было показано в этой экспериментальной работе.

^(**) Хотя на обывательском уровне слова «хаотичный» и «случайный» часто используются как синонимы, на уровне физики эти понятия существенно отличаются: хаотические системы являются детерминированными – это системы, движение которых описывается строго определенными уравнениями, не подвержено воздействию случайных факторов и потому предопределено начальными условиями. Однако трудность предсказания движения хаотических систем делает их на практике похожими на случайные.

^(***) Еще один пример интегрируемого бильярда – это бильярд в форме эллипса. В этом случае симметрия, делающая его интегрируемым, уже не столь очевидна, как в случае круга и прямоугольника.

^(****) Если выражаться более точно, то принадлежность бильярда к интегрируемым или хаотическим зависит от числа независимых интегралов движения – сохраняющихся с течением времени величин. Интегрируемые бильярды обладают двумя интегралами движения, в двумерной системе этого достаточно для точного аналитического решения уравнений движения. Хаотический бильярд имеет только один интеграл движения – кинетическую энергию шарика.

Как приготовить тарелку Хладни

Хотите свою тарелку Хладни? Вот как!

ПОСМОТРЕТЬ ВИДЕО

Другие интересные демонстрации:

Как сделать вихревую пушку

Как построить башню из лиры

Как сделать гравитационный колодец

Обучаемые темы:

резонанс
колебания
уравнения в частных производных

Теория:

Пластины Хладни — отличный инструмент для визуализации резонансных структур в двух измерениях. Понять, как они работают, намного проще, чем понять теорию и математику, лежащую в основе самих паттернов, поэтому здесь мы сконцентрируемся на этом.

Давайте начнем с простого одномерного примера. Если заставить струну вибрировать на особой резонансной частоте (определяемой длиной, плотностью и натяжением струны), стоячая волна будет иметь места по всей длине, где струна вообще не будет двигаться. Эти места называются «узлами». Повсюду струна вибрирует, двигаясь вверх и вниз, назад и вперед очень быстро. Если бы мы смогли сбалансировать немного песка на струне, песок, удаленный от узлов, был бы выброшен в космос, а песок на узле остался бы счастливо там, где он есть.

В то время как расчет резонансных частот одномерной струны довольно прост, теоретические детали в двух измерениях становятся намного сложнее. Но мы можем легко увидеть закономерности, используя метод, описанный ниже. Пластина Хладни представляет собой жесткий тонкий кусок металла, обычно правильной формы, но не обязательно такой. Пластина прикреплена к источнику вибрации. Источник должен быть достаточно сильным, чтобы вибрировать плиту достаточно, чтобы раскачать песок по линиям нулевой амплитуды (узловым линиям). В идеале источник также должен иметь возможность охватывать широкий частотный диапазон, поэтому исследуйте все возможные закономерности.

Эти узоры, особенно на более высоких частотах, демонстрируют удивительную сложность и симметрию. Если вы можете выдержать шум, легко часами искать новые узоры на песке.

Процедура:

Поместите динамик/драйвер на пластиковый поднос. Поднос значительно облегчит последующую уборку!
Не касайтесь верхней поверхности планшета. Отпечатки пальцев (масла) заставят песок «прилипнуть» к поверхности, что затруднит получение красивых узоров. Предварительно протрите поверхность метанолом, чтобы убедиться, что она идеально чистая.
Сбалансируйте пластину на стойке динамика.
Посыпьте поверхность небольшим количеством «живописного песка».
Включите генератор волн и увеличьте выходную амплитуду примерно наполовину.
Паттерны наблюдались в диапазоне от 500 Гц до 5000 Гц. Лучший диапазон для показа в классе — от 2000 до 3000 Гц. В этом диапазоне есть много паттернов, очень близких по частоте, с удивительной сложностью.

Безопасность:

Следите за тем, чтобы в динамик не попал песок!
Следует использовать средства защиты органов слуха, так как звук из динамика может стать раздражающе громким.

Пред.
Следующий

Вы здесь:
Главный
Инструкции
Как сделать тарелку Хладни

Как ваять звук в фигурки Хладни : Makery

Опубликовано 9 мая 2017 г. по Николя Барриал

Звуковые волны скрывают странные узоры, впервые обнаруженные в XIX веке основоположником современной акустики Эрнстом Хладни, который использовал вибрирующую пластину. Протестируйте самодельную версию, придуманную сооснователем бельгийского хакерского пространства.

Звук неизвестен, о чем свидетельствует само его определение: «механическая вибрация жидкости, распространяющаяся в виде волн». Какая жидкость? Воздух, конечно! Но настоящим сюрпризом является то, что в зависимости от интенсивности вибрации волны образуют разные узоры. Фигуры Хладни были открыты в 19 веке немецким физиком Эрнстом Хладни, который с помощью лука создавал волну на медной пластине, покрытой песком.

Теперь вы тоже можете пережить этот момент озарения, создав тарелку Хладни, переработанную 25-летним бельгийским мастером Лоиком, также известным как Iooner, разработчиком и соучредителем Liege Hackerspace. Нас очень вдохновил урок в его блоге.

Материалы

– 1 громкоговоритель
– 1 кусок дерева (15 X 15 см)
– 1 пластина из оргстекла (15 X 15 см)
– 1 тонкая алюминиевая пластина (20 X 20 см)
– 1 крышка от пластиковой бутылки
– 9 длинных болты (5 мм) и 10 гаек (5 мм)
– Паяльник, дрель (5 мм), клей, резак
– 1 усилитель или система Hi-Fi и аудиокабели

Размер пластин соответствует размеру динамика.

Шаг 1: Подготовьте динамик С помощью резака снимите мембрану и крышку магнита с динамика. © Iooner CC-by-SA Припаяйте к динамику новый аудиокабель. © Iooner CC-by-SA

Шаг 2: Подготовьте основание Вставьте винты в кусок дерева, чтобы закрепить динамик. © Iooner CC-by-SAPПроткните крышку бутылки дрелью и вставьте болт между двумя гайками. © Iooner CC-by-SAS Прикрепите динамик к основанию с помощью гаек и болтов, затем приклейте стержень с крышкой к центру. © Iooner CC-by-SA

Шаг 3: Подготовьте пластину Прикрепите пластину из плексигласа к болтам над динамиком, затем прикрепите алюминиевую пластину к ножке над ней. © Iooner CC-by-SASВид сбоку для оценки расстояний между каждым слоем. © Iooner CC-by-SA

Шаг 4: Подключи и работай

Подключите динамик к усилителю. Посыпьте алюминиевую пластину небольшим количеством мелкого песка или сахара. Вы можете использовать мобильное или настольное приложение для генерации определенных частот.