Многоугольник — Википедия
Материал из Википедии — свободной энциклопедии
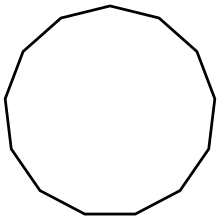 Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.
Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.
 Многоугольники
МногоугольникиСуществуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется
В любом случае вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Связанные определения[править | править код]
- Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
- Стороны многоугольника называются смежными, если они прилегают к одной вершине.
- Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
- Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
- Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.
- Выпуклый многоугольник это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника.
- Выпуклый многоугольник называется правильным, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник.
- Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником, например, пентаграмма и октаграмма.
- Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
- Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
- Сумма внутренних углов плоского n{\displaystyle n}-угольника без самопересечений равна (n−2)⋅180∘{\displaystyle (n-2)\cdot 180^{\circ }}.
- Число диагоналей всякого n{\displaystyle n}-угольника равно n⋅(n−3)2{\displaystyle {\tfrac {n\cdot (n-3)}{2}}}.
Площадь[править | править код]
- Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} — последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:
- S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.
Квадрируемость фигур[править | править код]
С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.
- Многогранник — обобщение многоугольника в размерности три, замкнутая поверхность, составленная из многоугольников, или тело, ей ограниченное.
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Геометрические фигуры из многоугольников для дошкольников
Геометрические фигуры для дошкольников могут быть сложным материалом, если подать его не правильно. Язык геометрических фигур состоит из простых элементов, из которых можно даже составлять рисунки. В игровой форме можно изучить, чем похожи все фигуры, составить рисунок из многоугольников и треугольников. Виды прямоугольников, изображения треугольной пирамиды, составленные из фигур рисунки и другие картинки для изучения материала можно скачать в этой статье.

Картинка из прямоугольников.
Рисунок из многоугольников.
Виды фигур по геометрии.
Паровоз из треугольников, кружков и прямоугольников.
Язык геометрических фигур.
Назови многоугольники.
Для класса.
Треугольная пирамида.
Подпиши названия этих фигур.
Виды четырёхугольников.
Простой рисунок для детского сада.
Какая фигура лишняя?
Составить рисунок из геометрических фигур не сложно.
Цветными карандашами.
Раскраска.
Прямоугольник — это четырехугольник, у которого все углы прямые.
Разрезные картинки для дошкольников.
Многоугольники. Видеоурок. Геометрия 8 Класс
Тема: Четырехугольники
Урок: Многоугольники
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах –
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).

Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
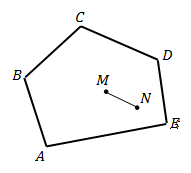
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение.Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение.Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике 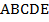 , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка
, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка 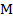
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.
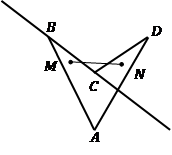
Рис. 3. Невыпуклый многоугольник
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми
являются все остальные многоугольники.Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через 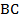 в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков 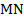
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
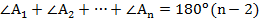 , где
, где  – количество его углов (сторон).
– количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
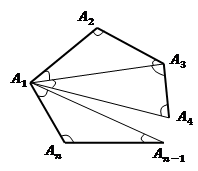
Рис. 4. Выпуклый n-угольник
Из вершины 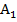 проведем все возможные диагонали. Они делят n-угольник на
проведем все возможные диагонали. Они делят n-угольник на 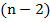 треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине
треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине 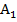 . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника –
. Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – 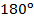 , то сумма внутренних углов n-угольника:
, то сумма внутренних углов n-угольника:
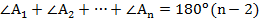 , что и требовалось доказать.
, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.
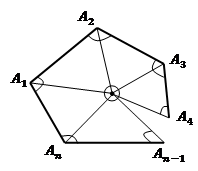
Рис. 5.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол 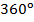 . Имеем:
. Имеем:
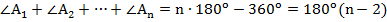 , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике 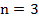 , а сумма углов
, а сумма углов  . В четырехугольнике
. В четырехугольнике 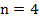 , а сумма углов –
, а сумма углов – 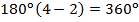 и т.д.
и т.д.
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
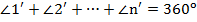 , где
, где 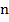 – количество его углов (сторон), а
– количество его углов (сторон), а 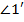 , …,
, …, 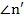 – внешние углы.
– внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.

Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то 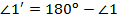 и аналогично для остальных внешних углов. Тогда:
и аналогично для остальных внешних углов. Тогда:
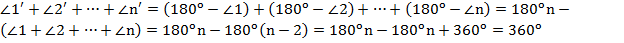 .
.
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника 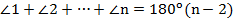 .
.
Доказано.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна 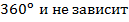 от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Profmeter.com.ua (Источник).
- Narod.ru (Источник).
- Xvatit.com (Источник).
Домашнее задание
- № 43, 42 (а, б, в, г, з), 46 (а, б), 47 (а,б). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Существует ли выпуклый многоугольник, сумма углов которого равна: а)
 ; б)
; б)  ; в)
; в)  ?
? - Найдите углы четырехугольника, если они пропорциональны числам 2, 3, 10 и 21. Выпуклый или невыпуклый этот четырехугольник?
- Вершины выпуклого пятиугольника соединены через одну. Найдите сумму углов при вершинах полученной «звезды».
Многоугольник — определение и основные понятия, виды и свойства фигур
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
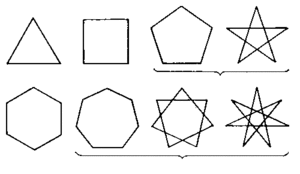
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
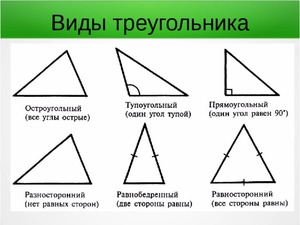
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
- Равносторонние — у которых длина всех отрезков одинаковая.
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
Кроме того, принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
Виды многоугольников
Виды многоугольников:
Четырехугольники
Четырехугольники, соответственно, состоят из 4-х сторон и углов.
Стороны и углы, расположенные напротив друг друга, называются противоположными.
Диагонали делят выпуклые четырехугольники на треугольники (см. на рисунке).
Сумма углов выпуклого четырехугольника равна 360° (по формуле: (4-2)*180°).
Параллелограммы
Параллелограмм — это выпуклый четырехугольник с противоположными параллельными сторонами (на рис. под номером 1).
Противоположные стороны и углы в параллелограмме всегда равны.
А диагонали в точке пересечения делятся пополам.
Трапеции
Трапеция — это тоже четырехугольник, и в трапеции параллельны только две стороны, которые называются основаниями. Другие стороны — это боковые стороны.
Трапеция на рисунке под номером 2 и 7.
Как и в треугольнике:
— если боковые стороны равны, то трапеция — равнобедренная;
— если один из углов прямой, то трапеция — прямоугольная.
Средняя линия трапеции равна полусумме оснований и параллельна им.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Помимо свойств параллелограмма, ромбы имеют своё особое свойство — диагонали ромба перпендикулярны друг другу и делят углы ромба пополам.
На рисунке ромб под номером 5.
Прямоугольники
Прямоугольник — это параллелограмм, у которого каждый угол прямой (см. на рис. под номером 8).
Помимо свойств параллелограмма, прямоугольники имеют своё особое свойство — диагонали прямоугольника равны.
Квадраты
Квадрат — это прямоугольник, у которого все стороны равны (№4).
Обладает свойствами прямоугольника и ромба (так как все стороны равны).
Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянноДобавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
Выпуклый многоугольник — Википедия
Материал из Википедии — свободной энциклопедии

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Существует множество эквивалентных определений:
- многоугольник является выпуклым, если часть плоскости, им ограниченная (плоский многоугольник) является выпуклым множеством;
- многоугольник будет выпуклым, если для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём;
- многоугольник, для которого продолжения сторон не пересекают других его сторон;
- многоугольник без самопересечений, каждый внутренний угол которого не более 180°;
- многоугольник, все диагонали которого полностью лежат внутри него;
- выпуклая оболочка конечного числа точек на плоскости;
- ограниченное множество, являющееся пересечением конечного числа замкнутых полуплоскостей.
- Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений. Тогда его площадь вычисляется по формуле:
- S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.
Многоугольники — урок. Геометрия, 8 класс.
Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.
Точки называются вершинами ломаной, а отрезки — звеньями ломаной.
Виды ломаных
Ломаная называется замкнутой, если у неё концы совпадают.

Если концы ломаной не совпадают, то она называется незамкнутой.

Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.
На следующем рисунке — ломаная с самопересечением.

Многоугольник
Многоугольник — это простая замкнутая ломаная линия и конечная часть
плоскости, которую она ограничивает.
Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.
\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.
Пятиугольник \(ABCDE\) является выпуклым многоугольником.
Сумма углов выпуклого \(n\)-угольника
В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.
Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.
Сумма внутренних углов любого треугольника равна 180°.
Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Пример:
вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.

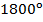 ; б)
; б) 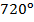 ; в)
; в) 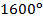 ?
?