| ЗНАК | ЗНАЧЕНИЕ | ПРИМЕР |
| = | равно | 5 = 5 |
| ≠ | не равно | 7 ≠ 5 |
| ≈ | приблизительно | 3,57 ≈ 3,6 |
| >, | больше, меньше | 8 > 5 |
| ≥ | больше или равно | a ≥ b |
| ≤ | меньше или равно | c ≤ b |
| + | плюс | 6 + 4 = 10 |
| — | минус | 10 — 6 = 4 |
| * | умножение | 5 * 3 = 15 |
| : | деление | 15 : 3 = 5 |
| ! | факториал | 3! = 1*2*3 = 6 |
| ∑ | сумма | |
| ⋅ | Оператор точка | |
| ⋆ | Оператор звезда | |
| ⊙ | Оператор точка в круге | |
| ⊚ | Оператор круг в круге | |
| ⊛ | Оператор звездочка в круге | |
| − | Знак минус | |
| ± | Знак плюс-минус | |
| ∓ | Знак минус-плюс | |
| ∔ | Знак точка-плюс | |
| × | Знак умножения | |
| ÷ | Знак деления | |
| ∞ | Знак бесконечность | |
| ˔ | Знак перпендикулярно | |
| ∼ | Оператор тильды (подобно) | |
| ∽ | Знак обратная тильда | |
| ≁ | Знак не тильда | |
| ≂ | Знак минус тильда | |
| ≃ | Знак асимптотически равный | |
| ≄ | Знак асимптотически равный | |
| ≈ | Знак почти равный (приблизительно) | |
| ≉ | Знак почти не равный | |
| ≊ | Знак равный или почти равный | |
| ≋ | Тройная тильда | |
| ≌ | Знак все равны | |
| ≅ | Знак приблизительно равный | |
| ≆ | Знак фактически равный | |
| ≇ | Знак фактически не равный | |
| ≠ | Знак не равно | |
| > | Знак больше | |
| < | Знак меньше | |
| ≤ | Знак меньше или равно | |
| ≥ | Знак больше или равно | |
| ≦ | Меньше, чем над равно | |
| ≧ | Больше, чем над равно | |
| ≨ | Менее чем, но не равны | |
| ≩ | Больше чем, но не равны | |
| ≮ | Не меньше чем | |
| ≯ | Не больше чем | |
| ⋦ | Меньше чем, но не эквивалентны | |
| ⋧ | Больше чем, но не эквивалентны | |
| ⋖ | Меньше чем с точкой | |
| ⋗ | Больше чем с точкой | |
| ≰ | Ни меньше, ни равный | |
| ≱ | Ни больше, ни равный | |
| ⋜ | Равно или меньше чем | |
| ⋝ | Равно или больше чем | |
| ≲ | Меньше чем или эквивалентно | |
| ≳ | Больше чем или эквивалентно | |
| ≶ | Меньше чем или больше чем | |
| ≷ | Больше чем или меньше чем | |
| ≸ | Ни меньше чем, ни больше чем | |
| ≹ | Ни больше чем, ни меньше чем | |
| ⋚ | Меньше или равно или больше чем | |
| ⋛ | Больше или равно или меньше чем | |
| ≡ | Знак тождественно | |
| ≢ | Знак не идентично | |
| ≀ | Сплетение | |
| ≍ | Знак эквивалентно | |
| ≏ | Знак различие между | |
| ≣ | Строго эквивалентный | |
| ≪ | Гораздо меньше чем | |
| ≫ | Гораздо больше чем | |
| ⋘ | Много меньше чем | |
| ⋙ | Много больше чем | |
| ¬ | Знак отрицания (скобка) | |
| ∀ | Для всех | |
| ∂ | Частичный дифференциал | |
| ∃ | Существует | |
| ∄ | Не существует | |
| ∆ | Инкремент | |
| ∇ | Оператор набла | |
| ∈ | Элемент из | |
| ∉ | Не элемент из | |
| ∋ | Содержит в качестве члена | |
| ∌ | Не содержит как член | |
| √ | Квадратный корень | |
| ∛ | Кубический корень | |
| ∜ | Четвертый корень | |
| ∝ | Знак пропорционально | |
| ∠ | Знак угол | |
| ∟ | Прямой угол | |
| ⊾ | Прямой угол с дугой | |
| ∡ | Измеренный угол | |
| ∣ | Разделять | |
| ∤ | Не разделять | |
| ∥ | Параллельно | |
| ∦ | Не параллельно | |
| ∧ | Логическое «И» | |
| ∨ | Логическое «Или» | |
| ∩ | Пересечение | |
| ∪ | Союз (объединение) | |
| ∫ | Интеграл | |
| ∬ | Двойной интеграл | |
| ∭ | Тройной интеграл | |
| ∮ | Контурный интеграл | |
| ∯ | Поверхностный интеграл | |
| ∴ | Следовательно | |
| ∵ | Поскольку | |
| ∶ | Соотношение | |
| ∷ | Пропорция | |
| ∸ | Точка минус | |
| ∹ | Избыток | |
| ∺ | Геометрическая прогрессия | |
| ⊂ | Подмножество | |
| ⊃ | Супермножество | |
| ′ | Штрих | |
| ″ | Двойной штрих | |
| ‴ | Тройной штрих | |
| ½ | Одна вторая | |
| ℃ | Знак градуса по Цельсию | |
| N | натуральные числа | 1,2,3,4,5…. |
| Z | целые числа | -1,0,+1,+2 |
| R | рациональные числа |
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
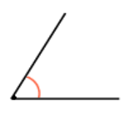 | острый угол | угол от 0 до 90 градусов | ∠AOB = 60° |
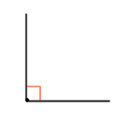 | прямой угол | угол, равный 90 граусам | ∠AOB = 90° |
 | тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° |
 | развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) | градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единици измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единици измерения угла, 1′ = 60″ | α = 70°59′59″ |
 | линия | бесконечная прямая без начала и конца | |
 | отрезок | участок на прямой между точками A и B | |
 | луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | |
 | дуга | дуга, образованная между точками A и B | |
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| ∥ | параллельность | непересекающиеся прямые (линии) | AB ∥ CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность | элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, c = π⋅d = 2⋅π⋅r | π = 3.141592654… |
| рад (rad) или c | радиан | единица измерения угла | 360° = 2π c |
Математический знаки и символы
«Символы не являются только записью мыслей,
средством её изображения и закрепления, –
нет, они воздействуют на самую мысль,
они… направляют её, и бывает достаточно
переместить их на бумаге… для того, чтобы
безошибочно достигнуть новых истин».
Л.Карно
Математические знаки служат в первую очередь для точной (однозначно определённой) записи математических понятий и предложений. Их совокупность в реальных условиях их применения математиками составляет то, что называется, математическим языком.
Математические знаки позволяют записывать в компактной форме предложения, громоздко выраженные на обычном языке. Это облегчает их запоминание.
Прежде чем использовать в рассуждениях те или иные знаки, математик старается сказать, что каждый из них обозначает. Иначе его могут не понять.
Но математики не всегда могут сказать сразу, что отражает тот или иной символ, введённый ими для какой-либо математической теории. Например, сотни лет математики оперировали отрицательными и комплексными числами, однако объективный смысл этих чисел и действие с ними удалось раскрыть лишь в конце XVIII и в начале XIX века.
1. Символизм математических кванторов
Подобно обычному языку, язык математических знаков позволяет обмениваться установленными математическими истинами, но являясь лишь вспомогательным средством, присоединяемым к обычному языку и без него существовать, не может.
Математическое определение:
На обычном языке:
Пределом функции F (x) в некоторой точке X0 называется постоянное число А, такое что для произвольного числа Е>0 существует такое положительное d(E), что из условия |X – X0|<d вытекает неравенство |F(x)–A|<E
Запись в кванторах (на математическом языке)
|
2. Символизм математических знаков и геометрических фигур.
1) Бесконечность — концепция, используемая в математике, философии и естественных науках. Бесконечность какого-то понятия или атрибута некоторого объекта означает невозможность указать для него границы или количественную меру. Термин бесконечность соответствует нескольким различным понятиям, в зависимости от области применения, будь то математика, физика, философия, теология или повседневная жизнь. В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы. К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие, а целые числа включены в действительные. Таким образом, в этом случае одно кардинальное число (равно мощности множества) «бесконечнее» другого. Основоположником этих понятий был немецкий математик Георг Кантор. В математическом анализе ко множеству действительных чисел добавляются два символа, плюс и минус бесконечность, применяющиеся для определения граничных значений и сходимости. Нужно отметить, что в этом случае речь об «осязаемой» бесконечности не идёт, так как любое утверждение, содержащее этот символ, можно записать, используя только конечные числа и кванторы. Эти символы (как и многие другие) были введены для сокращения записи более длинных выражений. Бесконечность также неразрывно связана с обозначением бесконечно малого, к примеру, ещё Аристотель сказал:
- время,
- разделение величин,
- неиссякаемость творящей природы,
- само понятие границы, толкающее за её пределы,
- мышление, которое неостановимо.
Бесконечность в большинстве культур появилась как абстрактное количественное обозначение чего-то непостижимо большого, в применении к сущностям без пространственных или временных границ.
Далее бесконечность получила развитие в философии и теологии наравне с точными науками. К примеру, в теологии бесконечность Бога не столько даёт количественное определение, сколько означает неограниченность и непостижимость. В философии это атрибут пространства и времени.
2) Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку. Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
3) Квадрат (ромб) – является символом комбинации и упорядочивания четырёх различных элементов, например четыре основных стихий или четырёх времён года. Символ числа 4, равенства, простоты, прямоты, истины, справедливости, мудрости, чести. Симметрия является той идеей посредством которой человек пытается постичь гармонию и с давних времён считалась символом прекрасного. Симметрией обладают так называемые “фигурные” стихи, текст которых имеет очертание ромба.
Стихотворение – ромб.
Мы –
Среди тьмы.
Глаз отдыхает.
Сумрак ночи живой.
Сердце жадно вздыхает,
Шепот звёзд долетает порой.
И лазурные чувства теснятся толпой.
Всё забылось в блеске росистом.
Поцелуем душистым!
Поскорее блесни!
Снова шепни,
Как тогда:
«Да!»(Э.Мартов, 1894г)
4) Прямоугольник. Из всех геометрических форм это наиболее рациональная, наиболее надёжная и правильная фигура; эмпирически это объясняется тем фактом, что всегда и везде прямоугольник был излюбленной формой. С помощью него человек приспосабливал пространство или какой-либо предмет для непосредственного использования в своём быту, например: дом, комната, стол, кровать и т.п.
5) Пентагон – правильный пятиугольник в виде звезды символ вечности, совершенства, вселенной. Пентагон – амулет здоровья, знак на дверях для того, чтобы отогнать ведьм, эмблема Тота, Меркурия, кельтского Гавайна и др., символ пяти ран Иисуса Христа, благополучия, удачи у евреев, легендарный ключ Соломона; знак высокого положения в обществе у Японцев.
6) Правильный шестиугольник, гексагон – символ изобилия, красоты, гармонии, свободы, брака, символ числа 6, образ человека (две руки, две ноги, голова и туловище).
7) Крест – символ высших сакральных ценностей. Крест моделирует духовный аспект, восхождение духа, устремление к богу, к вечности. Крест – универсальный символ единства жизни и смерти.
Конечно, с этими утверждениями можно и не соглашаться.
Однако никто не будет отрицать, что любое изображение вызывает у человека ассоциации. Но проблема в том, что одни предметы, сюжеты или графические элементы вызывают у всех людей (вернее, у многих) одинаковые ассоциации, а другие – совершенно различные.
8) Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Свойства треугольника как фигуры: прочность, неизменяемость.
Аксиома А1 стереометрии гласит: «Через 3 точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна!»
Чтобы проверить глубину понимания этого утверждения обычно задают задачу на засыпку: «На столе сидят три мухи, на трёх концах стола. В определённый момент они разлетаются по трём взаимно – перпендикулярным направлениям с одинаковой скоростью. Когда они снова окажутся в одной плоскости?». Ответом служит тот факт, что три точки всегда, в любой момент, определяют единственную плоскость. И именно 3 точки определяют треугольник, поэтому эта фигура в геометрии считается самой устойчивой и прочной.
9) Шестиконечная Звезда (Звезда Давида) – состоит из двух наложенных один на другой равносторонних треугольников. Одна из версий происхождения знака связывает его форму с формой цветка Белой лилии, имеющего шесть лепестков. Цветок традиционно располагался под храмовым светильником, таким образом, что священник зажигал огонь, как бы, в центре Маген Давида. В каббале два треугольника символизируют свойственную человеку дуальность: добро против зла, духовное против физического и так далее. Треугольник, направленный остриём вверх, символизирует наши добрые дела, которые поднимаются на небеса и вызывают поток благодати, нисходящий обратно в этот мир (что символизирует треугольник, направленный вниз). Иногда Звезду Давида называют Звездой Творца и связывают каждый из её шести концов с одним из дней недели, а центр – с субботой.
10) Пятиконечная Звезда – Основной отличительной эмблемой большевиков является красная пятиконечная звезда, официально установленная весной 1918 года. Первоначально большевистская пропаганда назвала её “ Марсовой звездой” ( якобы принадлежащей античному богу войны – марсу), а затем стала заявлять, что “ Пять лучей звезды, означает союз трудящихся всех пяти континентов в борьбе против капитализма”. В действительности же пятиконечная звезда не имеет никакого отношения ни к воинствующему божеству Марсу, ни к международному пролетариату, это – древний оккультный знак (очевидно ближневосточного происхождения), называющийся “пентаграммой” или “Звездой Соломона”.
Правительству”, находящемуся под полным контролем масонства.
Весьма часто сатанисты рисуют пентаграмму двумя концами вверх, чтобы туда было легко вписать дьявольскую голову “Пентаграмма Бафомета”. Портрет “Пламенного революционера” помещён внутри “Пентаграммы Бафомета”, являющейся центральной частью композиции проектируемого в 1932 году особого чекистского ордена “ Феликса Дзержинского” (далее проект был отклонён Сталиным, глубоко ненавидящим “Железного Феликса”).
Отметим, что зачастую пентаграмма размещалась большевиками на красноармейском обмундировании, в военной технике, различных знаках и всевозможных атрибутах наглядной агитации чисто по-сатанински: двумя “рогами” вверх.
Марксистские планы “всемирной пролетарской революции” имели явно масонское происхождение, ряд виднейших марксистов состоял в масонстве. К ним относился Л.Троцкий, именно он и предложил сделать масонскую пентаграмму опознавательной эмблемой большевизма.
Интернациональные масонские ложи тайно оказывали большевикам всестороннюю поддержку, особенно финансовую.
3. Масонские знаки
Масоны
Девиз: «Свобода. Равенство. Братство».
Общественное движение свободных людей, которые на основе свободного выбора позволяют стать лучше, стать ближе к богу следственно, они признаны улучшить мир.
Масоны – соратники Творца, сподвижники общественного прогресса, против инерции, косности и невежества. Выдающиеся представители масонства – Карамзин Николай Михайлович, Суворов Александр Васильевич, Кутузов Михаил Илларионович, Пушкин Александр Сергеевич, Геббельс Иозеф.
Знаки
Лучезарное око (дельта) – знак древний, религиозный. Он говорит о том, что Бог надзирает над творениями своими. Изображением этого знака масоны спрашивали у Бога благословения на какие-либо грандиозные действия, на труды свои. Лучезарное око расположено на фронтоне Казанского Собора в Санкт-Петербурге.
Сочетание циркуля и угольника в масонском знаке.
Для непосвящённого – это орудие труда (каменщика), а для посвящённых – это способы познания мира и соотношения божественной премудрости и человеческого разума.
Угольник, как правило, снизу – это человеческое познание мира. С точки зрения масонства, человек приходит в мир, что познать божественный замысел. А для познания необходим инструментарий. Самая эффективная наука в познание мира – математика.
Угольник – древнейший математический инструмент, известный с незапамятных времён. Градуировка угол
Неравенство — Википедия
Нера́венство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков[1].
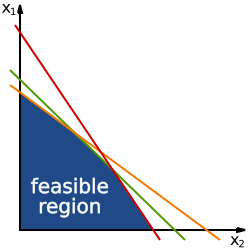
Область допустимых решений («feasible region») в задачах линейного программирования
- Строгие неравенства
Неравенства a>b{\displaystyle a>b} и b<a{\displaystyle b<a} равносильны. Говорят, что знаки >{\displaystyle >} и <{\displaystyle <} противоположны; например, выражение «знак неравенства сменился на противоположный» означает, что <{\displaystyle <} заменено на >{\displaystyle >} или наоборот.
- Нестрогие неравенства
Русскоязычная традиция начертания знаков ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } отличается от принятой за рубежом, где обычно используются знаки ≤{\displaystyle \leq } и ≥{\displaystyle \geq }. Про знаки ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } также говорят, что они противоположны.
- Другие типы неравенств
Далее в данной статье, если не оговорено иное, понятие неравенства относится к первым 4 типам.
В элементарной математике изучают числовые неравенства. В общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы.
Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»).
Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:
- a<b<c{\displaystyle a<b<c} — это краткая запись пары неравенств: a<b{\displaystyle a<b} и b<c.{\displaystyle b<c.}
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных (x,y,…).{\displaystyle (x,y,\dots ).} Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство 18x<414{\displaystyle 18x<414} — алгебраическое первой степени, неравенство 2×3−7x+6>0{\displaystyle 2x^{3}-7x+6>0} — алгебраическое третьей степени, неравенство 2x>x+4{\displaystyle 2^{x}>x+4} — трансцендентное[2].
Свойства[править | править код]
Свойства числовых неравенств в некоторых отношениях близки к свойствам уравнений[1]:
- К обеим частям неравенства можно прибавить одно и то же число.
- От обеих частей неравенства можно отнять одно и то же число. Следствие: как и для уравнений, любой член неравенства можно перенести в другую часть с противоположным знаком. Например, из a+b<c{\displaystyle a+b<c} следует, что a<c−b.{\displaystyle a<c-b.}
- Обе части неравенства можно умножить на одно и то же положительное число.
- Одноимённые неравенства можно складывать: если, например, a<b{\displaystyle a<b} и c<d,{\displaystyle c<d,} то a+c<b+d.{\displaystyle a+c<b+d.} Неравенства с противоположными знаками можно аналогично почленно вычитать.
- Если все четыре части двух неравенств положительны, то неравенства можно перемножить.
- Если обе части неравенства положительны, то их можно возвести в одну и ту же (натуральную) степень, а также логарифмировать с любым основанием (если основание логарифма меньше 1, то знак неравенства надо изменить на противоположный).
- Другие свойства
- (Транзитивность) Если a<b{\displaystyle a<b} и b<c,{\displaystyle b<c,} то a<c{\displaystyle a<c} и аналогично для прочих знаков.
- Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный: больше на меньше, больше или равно на меньше или равно и т. д.
Решение неравенств[править | править код]
Если неравенство содержит символы неизвестных, то решение его означает выяснение вопроса, при каких значениях неизвестных неравенство выполняется. Примеры:
- x2<4{\displaystyle x^{2}<4} выполняется при −2<x<2.{\displaystyle -2<x<2.}
- x2>4{\displaystyle x^{2}>4} выполняется, если либо x>2,{\displaystyle x>2,} либо x<−2.{\displaystyle x<-2.}
- x2<−4{\displaystyle x^{2}<-4} не выполняется никогда (решений нет).
- x2>−4{\displaystyle x^{2}>-4} выполняется при всех x{\displaystyle x} (тождество).
Внимание: если возвести в чётную степень неравенство, содержащее неизвестные, могут появиться «лишние» решения. Пример: если неравенство x>3{\displaystyle x>3} возвести в квадрат: x2>9,{\displaystyle x^{2}>9,} то появится ошибочное решение x<−3,{\displaystyle x<-3,} не удовлетворяющее исходному неравенству. Поэтому все полученные таким образом решения следует проверить подстановкой в исходное неравенство.
Неравенства первой степени[править | править код]
Неравенство первой степени имеет общий формат: ax>b{\displaystyle ax>b} или ax<b,{\displaystyle ax<b,} где a≠0{\displaystyle a\neq 0} (работа со знаками ⩾{\displaystyle \geqslant } и ⩽{\displaystyle \leqslant } аналогична). Чтобы его решить, разделите неравенство на a{\displaystyle a} и, если a<0,{\displaystyle a<0,} измените знак неравенства на противоположный[3]. Пример:
- 5x−11>8x+1.{\displaystyle 5x-11>8x+1.} Приведём подобные члены: −3x>12,{\displaystyle -3x>12,} или x<−4.{\displaystyle x<-4.}
Системы неравенств первой степени[править | править код]
Если одно и то же неизвестное входит более чем в одно неравенство, надо решить каждое неравенство в отдельности и затем сопоставить эти решения, которые должны выполняться все вместе.
Пример 1. Из системы {4x−3>5x−52x+4<8x{\displaystyle {\begin{cases}4x-3>5x-5\\2x+4<8x\end{cases}}} получаем два решения: для первого неравенства x<2,{\displaystyle x<2,} для второго: x>23.{\displaystyle x>{2 \over 3}.} Соединяя их, получаем ответ: 23<x<2.{\displaystyle {2 \over 3}<x<2.}
Пример 2. {2x−3>3x−52x+4>8x{\displaystyle {\begin{cases}2x-3>3x-5\\2x+4>8x\end{cases}}} Решения: x<2{\displaystyle x<2} и x<23.{\displaystyle x<{2 \over 3}.} Второе решение поглощает первое, так что ответ: x<23.{\displaystyle x<{2 \over 3}.}
Пример 3. {2x−3<3x−52x+4>8x{\displaystyle {\begin{cases}2x-3<3x-5\\2x+4>8x\end{cases}}} Решения: x>2{\displaystyle x>2} и x<23,{\displaystyle x<{2 \over 3},} они несовместимы, поэтому исходная система не имеет решений.
Неравенства второй степени[править | править код]
Общий вид неравенства второй степени (называемого также квадратным неравенством):
- x2+px+q>0{\displaystyle x^{2}+px+q>0} или x2+px+q<0.{\displaystyle x^{2}+px+q<0.}
Если квадратное уравнение x2+px+q=0{\displaystyle x^{2}+px+q=0} имеет вещественные корни x1,x2,{\displaystyle x_{1},x_{2},} то неравенство можно привести к виду соответственно:
- (x−x1)(x−x2)>0{\displaystyle (x-x_{1})(x-x_{2})>0} или (x−x1)(x−x2)<0.{\displaystyle (x-x_{1})(x-x_{2})<0.}
В первом случае x−x1{\displaystyle x-x_{1}} и x−x2{\displaystyle x-x_{2}} должны иметь одинаковые знаки, во втором — разные. Для окончательного ответа надо применить следующее простое правило[4].
Квадратный трёхчлен x2+px+q{\displaystyle x^{2}+px+q} с разными вещественными корнями отрицателен в интервале между корнями и положителен вне этого интервала. |
Если оказалось, что у уравнения x2+px+q=0{\displaystyle x^{2}+px+q=0} вещественных корней нет, то его левая часть сохраняет один и тот же знак при всех x.{\displaystyle x.} Поэтому исходное неравенство второй степени либо является тождеством, либо не имеет решений (см. ниже примеры[5]).
Пример 1. −2×2+14x−20>0.{\displaystyle -2x^{2}+14x-20>0.} Разделив на −2,{\displaystyle -2,} приведём неравенство к виду: x2−7x+10<0.{\displaystyle x^{2}-7x+10<0.} Решив квадратное уравнение x2−7x+10=0,{\displaystyle x^{2}-7x+10=0,} получаем корни x1=2;x2=5,{\displaystyle x_{1}=2;x_{2}=5,} поэтому исходное неравенство равносильно такому: (x−2)(x−5)<0.{\displaystyle (x-2)(x-5)<0.} Согласно приведенному выше правилу, 2<x<5,{\displaystyle 2<x<5,} что и является ответом.
Пример 2. −2×2+14x−20<0.{\displaystyle -2x^{2}+14x-20<0.} Аналогично получаем, что x−2{\displaystyle x-2} и x−5{\displaystyle x-5} имеют одинаковые знаки, то есть, согласно правилу, либо x<2,{\displaystyle x<2,} либо x>5.{\displaystyle x>5.}
Пример 3. x2+6x+15>0.{\displaystyle x^{2}+6x+15>0.} Уравнение x2+6x+15=0{\displaystyle x^{2}+6x+15=0} не имеет вещественных корней, поэтому левая часть его сохраняет знак при всех x.{\displaystyle x.} При x=0{\displaystyle x=0} левая часть положительна, поэтому исходное неравенство есть тождество (верно при всех x{\displaystyle x}).
Пример 4. x2+6x+15<0.{\displaystyle x^{2}+6x+15<0.} Как и в предыдущем примере, здесь левая часть всегда положительна, поэтому неравенство не имеет решений.
Аналогично, разложением на множители, можно решать неравенства высших степеней. Другой способ — построить график левой части и определить, какие знаки она имеет в различных интервалах[6].
Прочие неравенства[править | править код]
Существуют также дробно-рациональные, иррациональные, логарифмические и тригонометрические неравенства.
Ниже приведены практически полезные неравенства, тождественно выполняющиеся, если неизвестные попадают в указанные границы[7].
- (1+x)n⩾1+nx,{\displaystyle (1+x)^{n}\geqslant 1+nx,} где x⩾−1,n{\displaystyle x\geqslant -1,n} — натуральное число.
- |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|}
- См. следствия этого неравенства в статье Абсолютная величина.
Знаки неравенства в языках программирования[править | править код]
Символ «не равно» в разных языках программирования записывается по-разному.
| Символ | Языки |
|---|---|
| != | C, C++, C#, Java, JavaScript, Perl, PHP, Python, Wolfram Language |
| <> | Basic, Pascal |
| ~= | Lua |
| /= | Haskell, Fortran, Ada |
| # | Modula-2, Oberon |
