«Очень сложная задача по математике только для гениев» — Яндекс Кью
Математика и математики
Популярное
Сообщества
Задача по математике
Дана таблица 7 на 3, её заполняют ноликами и единичками. Если хотя бы на одном пересечении двух строк и столбцов все 4 цифры одинаковые, то заполнение таблицы считается неудачным. Можно ли заполнить эту таблицу так, чтобы избежать этого явления?
МатематикаДомашние заданияЗадачи
савелий повр
Математика и математики·
183
ОтветитьУточнитьАлександр Бражник
Математика
48
Люблю математику, люблю решать задачи и учиться. · 13 нояб 2021
Рассмотрим таблицу из семи строк и трёх столбцов. В нашей таблице семь строк, это значит, что в каждом столбце найдётся по крайней мере либо 4 нуля, либо 4 единицы. А поскольку столбцов три, то в двух из них будет по набору из не менее чем четырёх нулей или единиц. Рассмотрим эти два столбца и пусть в каждом из них не менее 4 нулей.
В нашей таблице семь строк, это значит, что в каждом столбце найдётся по крайней мере либо 4 нуля, либо 4 единицы. А поскольку столбцов три, то в двух из них будет по набору из не менее чем четырёх нулей или единиц. Рассмотрим эти два столбца и пусть в каждом из них не менее 4 нулей.
Тк в столбце 7 элементов, то найдётся строка в которой в этих столбцах будут нули. И такая строка должна быть одна. Иначе в этих двух столбцах и строчках будут нули.
Тогда в оставшихся шести строках этих двух столбцов будут стоять пары
0–1 или 1-0 . Ясно что хотя бы две одинаковые пары встретятся.
Таким образом, расставить правильным образом 0 и1 в таблице 7 на 3 невозможно.
Комментировать ответ…Комментировать…
Andrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 13 нояб 2021
7×3 явно какой-то избыточно невозможный случай.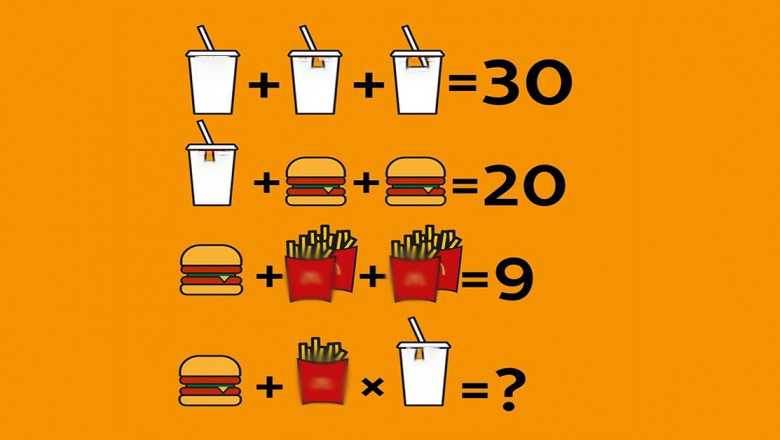
n×3 было можно так заполнить, а (n+1)×3 уже нельзя.
Александр Бражник
13 ноября 2021
4х3- это максимум 011 101 110 000 любая комбинация в пятой строке приводит к нарушению удачного расположения 0 и… Читать дальше
Комментировать ответ…Комментировать…
Andrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 13 нояб 2021
Почему не подходит, например: 000 010 000 010 000 010 ? Потому что, видимо две строки и два столбца не обязательно одинаковые, типа (1,3)×(1,3)? Читать далее
13 ноября 2021
Если у нас хотя бы две строки совпадают полностью, то неизбежно в них есть два столбца, которые совпадают по значен.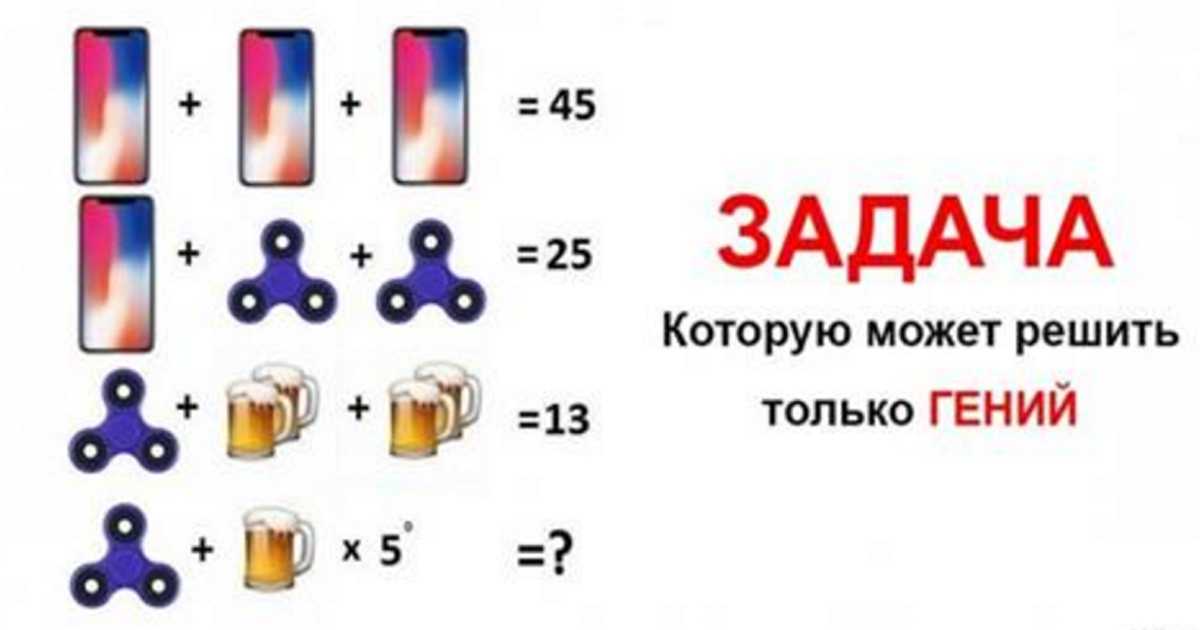 .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
О сообществе
Математика и математики
Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!
Только гений может набрать 5 из 10 в этом тесте IQ Ustaliy.ru
in Разные тесты
опубликовано Ульяна Грозная
Во время недавнего исследования учёные дали этот тест IQ 80 школьникам и ни один из них не смог правильно ответить более чем на 5 из 10 вопросов.
Удачи!
Вставить тест на сайт: HTML-код
Медведь
Крокодил
Булавка
Молоток
Гвоздь
Треугольник
Эллипс
Собака
Избыток
Богатство
Изобилие
Достаток
Имение
Хижина
Золотая рыбка
Дельфин
Летучая мышь
Прыжки
Ходьба
Упражнения
Треугольник
Параллелограмм
Прямоугольник
Квадрат
Кролик
Облако
Самолёт
Понравилось?
1. 6k Баллов
6k Баллов
Да Нет
iqлогикатест
Не пропустите
Как избежать опасностей на горнолыжном склоне: проходите наш тест на знание правил безопасности!
Наш тест на тему безопасности на горнолыжном склоне позволит вам проверить свои знания о правилах и мерах предосторожности, необходимых для того, чтобы избежать опасных ситуаций […] Больше
Тест: Угадай тиктокера по детской фотографии
Проверь свою интуицию! Для тебя собрали детские фотки тиктокеров — попробуй угадать, кто есть кто. Удачи! Пройти тест Вопрос из Знакомое лицо? Артур Бабич Олег […] Больше
Сможем ли мы угадать ваш знак Зодиака?
Ваш характер, интересы и предпочтения могут дать нам много информации о вашем знаке зодиака. Иногда простые ответы на вопросы могут дать подсказку о том, кто […] Больше
Тест: Сможешь вспомнить имена этих культовых музыкантов?
По фотографиям из теста необходимо определить, кто из музыкантов на на них изображён.
 Если вы считаете себя меломаном и при этом хорошо знаете всех знаковых […] Больше
Если вы считаете себя меломаном и при этом хорошо знаете всех знаковых […] БольшеТест: сможете ли вы выжить в дикой природе?
Вы еда или хищник? Давайте узнаем! Пройти тест Вопрос из Какое из этих растений вы бы съели? растение 1 растение 2 растение 3 Вопрос из […] Больше
Крутой тест на проверку состояния вашей памяти
Наша память — это мы сами: наша личность, наше отношение к людям, наши возможности, наше мышление — все связано с памятью. Начались проблемы с памятью? […] Больше
Насколько хорошая у вас память? Многие не могут пройти этот тест на «отлично»
Насколько хорошая у вас память? Выяснить это поможет прохождение теста. Пройти тест Вопрос из Включаем мозг и начинаем запоминать все детали на фото. Готовы? Поехали! […] Больше
Тест: Ты хорошо знаешь Эдисона Перца (EdisonPts)?
Хорошо ли ты знаешь Эдисона Перца ? Давай проверим это! Удачи! Пройти тест Вопрос из «Перец» это псевдоним или настоящая фамилия Эдисона? Настоящая фамилия Нет […] Больше
Тест: Что вы знаете о глютене и его вреде?
Наш мозг ежедневно атакуют вредные вещества, которые содержатся в самых обыкновенных продуктах.
 Любимые булочки, хлеб и макароны нет так уж безобидны. В их состав входит […] Больше
Любимые булочки, хлеб и макароны нет так уж безобидны. В их состав входит […] БольшеМы угадаем ваше любимое время года
Сейчас мы попробуем угадать ваше любимое время года! Пройти тест Вопрос из Насколько сильно вы переживаете о своей внешности? Сильнее, чем я готов признаться… Я […] Больше
Математические загадки Только самые умные могут решить
Возможно, вам захочется разбить калькулятор, потому что для решения этих хитрых математических загадок нужен гений.
Время математики!
Независимо от того, посещаете ли вы уроки математики регулярно или с тех пор, как вы последний раз возводили уравнение в квадрат, прошла минута, математические загадки предназначены для всех. От математики для взрослых (например, подсчета времени, когда нужно начать готовить, если индейка готовится 13 минут на фунт, а гости прибывают в 14:00) до решения головоломок судоку, математика является частью всей нашей жизни. Вам не нужно быть гением математики, чтобы решить эти головоломки. Мы ранжировали их от простых к сложным, чтобы вы могли разогреться с помощью более простых математических загадок и закончить настоящими головоломками. После всех этих вычислений вы будете готовы к еще более сложным загадкам. Нет ничего подобного этому «А-ха!» чувство, когда отгадываешь сложную загадку (или даже более легкую), так что приступим!
Вам не нужно быть гением математики, чтобы решить эти головоломки. Мы ранжировали их от простых к сложным, чтобы вы могли разогреться с помощью более простых математических загадок и закончить настоящими головоломками. После всех этих вычислений вы будете готовы к еще более сложным загадкам. Нет ничего подобного этому «А-ха!» чувство, когда отгадываешь сложную загадку (или даже более легкую), так что приступим!
Нэнси С. Росс/Getty Images
Простые математические загадки: Сумасшедшие восьмерки
Используя только сложение, сложите восемь восьмерок, чтобы получить число 1000.
Ответ:
888 + 88 + 8 + 8 + 8 = 1000. Это своего рода числовая загадка, которую вы можете решить с помощью таблицы умножения или простой логики. Во-первых, подойдите как можно ближе к 1000 (888). Отсюда легко догадаться об остальном.
СВЯЗАННЫЕ: Математические головоломки
Григорита Ко/Shutterstock
Легкие математические загадки: Фермерская жизнь В ответ на вопрос о животных на его ферме фермер говорит: «Я всегда держу только овец, коз и лошадей. На самом деле, на данный момент все они овцы, кроме трех, все козы, кроме четырех, и все лошади, кроме пяти». Сколько у него каждого животного?
На самом деле, на данный момент все они овцы, кроме трех, все козы, кроме четырех, и все лошади, кроме пяти». Сколько у него каждого животного?
Ответ:
У фермера 3 овцы, 2 козы и 1 лошадь. Вы можете решить эту простую математическую загадку с помощью быстрой гипотезы. Возьмем овец: мы знаем, что есть три животных, козы и лошади, поэтому мы предполагаем, что есть две козы и одна лошадь. Проверка этой гипотезы дает нам трех овец, что срабатывает, потому что есть четыре некозла: три овцы и одна лошадь! Теперь, когда вы знаете ответ на этот вопрос, попробуйте решить другие загадки о животных.
Africa Studio/Shutterstock
Легкие математические загадки: разница в возрастеОдин брат говорит о своем младшем брате: «Два года назад я был в три раза старше моего брата. Через три года я буду вдвое старше своего брата». Сколько им сейчас лет?
Ответ:
Один из способов решить эту математическую загадку — использовать четные числа: через три года старший брат будет в два раза старше своего младшего брата.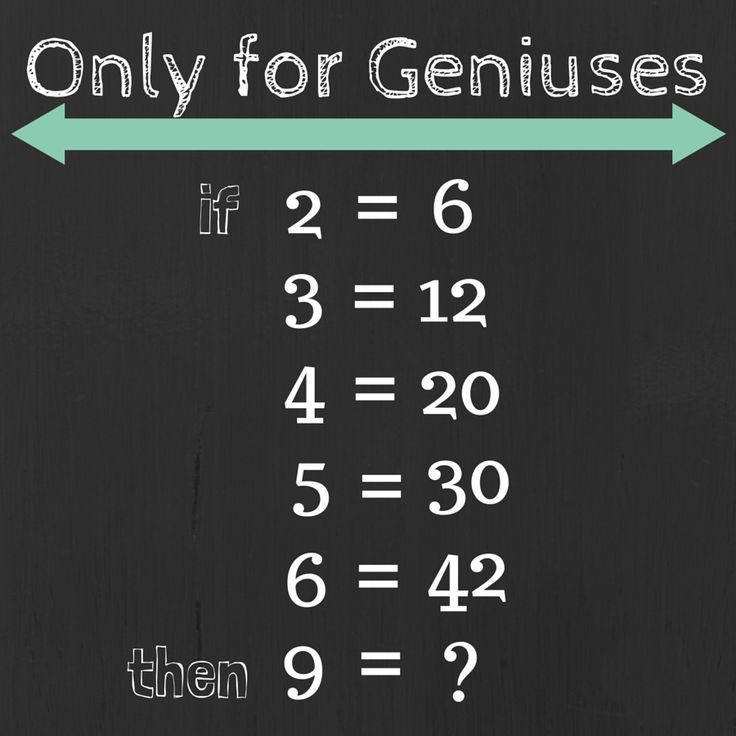 Это сразу исключает, что старшему брату в настоящее время 8, 11 и 14 лет, поэтому ему должно быть 17, а младшему брату 7. Два года назад им было 15 и 5 соответственно, а через три года им будет 20. и 10.
Это сразу исключает, что старшему брату в настоящее время 8, 11 и 14 лет, поэтому ему должно быть 17, а младшему брату 7. Два года назад им было 15 и 5 соответственно, а через три года им будет 20. и 10.
СВЯЗАННЫЕ: Логические головоломки
Джозеф Кларк/Getty Images
Легкие математические загадки: Загадочная задача
Я прибавляю шесть к одиннадцати и получаю пять. Почему это правильно?
Ответ:
Эта головоломка с числами создана, чтобы сбить вас с толку! Вы должны мыслить шире. Когда сейчас 11 часов утра, добавление шести часов дает 5 часов вечера. Прочтите эти загадки для взрослых, которые действительно проверят вашу сообразительность.
Daniel Grill/Getty Images
Легкие математические загадки: наследство Старая бабушка Адамс оставила половину своих денег внучке и половину этой суммы внуку. Она оставила шестую часть своему брату, а остаток, 1000 долларов, отдала собачьему приюту. Сколько всего она оставила?
Она оставила шестую часть своему брату, а остаток, 1000 долларов, отдала собачьему приюту. Сколько всего она оставила?
Ответ:
Это могло сбить вас с толку! Но хитрость заключается в том, чтобы сосредоточиться не на гипотетических суммах, а на дробях: сложение половины, четверти и одной шестой говорит нам, что сумма составляет долю двенадцатых (2+4+6=12). Вы также можете представить это как 6/12, 3/12, 2/12, что равняется 11/12. Если остаток составляет 1000 долларов, это должна быть одна двенадцатая, поэтому общая сумма составляет 12 000 долларов.
СВЯЗАННЫЕ: Лучшие загадки для детей
Илона Надь/Getty Images
Простые математические загадки: Какова частота?
Какая цифра чаще всего встречается между числами от 1 до 1000 включительно? Подсказка: ищите закономерность!
Ответ:
Самая распространенная цифра 1! Вы поняли, почему? Каждое число от 1 до 9 встречается ровно одинаковое количество раз в каждых десяти числах. Но поскольку мы включили число 1000, число 1 встречается дополнительно. Всего число 1 встречается 301 раз, а все остальные числа встречаются 300 раз.
Но поскольку мы включили число 1000, число 1 встречается дополнительно. Всего число 1 встречается 301 раз, а все остальные числа встречаются 300 раз.
georgeclerk/Getty Images
Легкие математические загадки: уравнение яйцаЕсли полдюжины куриц снесут полтора яйца за полтора дня, сколько яиц снесут полдюжины кур за полдюжины дней ?
Ответ:
Две дюжины. Если вы увеличите как количество кур, так и количество доступного времени в четыре раза (т. е. 1,5 умножить на 4, будет 6), количество яиц увеличится в 16 раз. 16 x 1,5 = 24.
СВЯЗАННЫЕ: Сможете ли вы найти недостающее число в этой головоломке?
DutchScenery/Getty Images
Сложные математические загадки: номера домовМой близнец живет напротив номера моего дома. Разница между номерами наших домов заканчивается на два. Каковы наименьшие возможные числа наших номеров домов?
Ответ:
Эти математические загадки решить непросто! Наименьшие возможные числа для домов 19 и 91.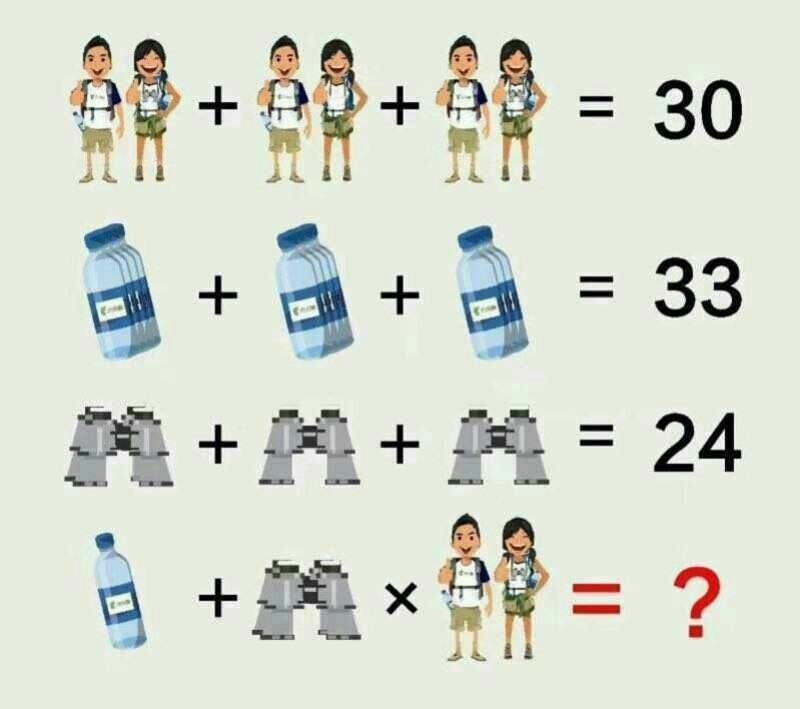 Разница 72.
Разница 72.
не определено не определено/Getty Images
Сложные математические загадки: Пребывание в отеле
Трое друзей отправляются в путешествие и снимают на ночь трехместный номер. Приехав в отель, они платят 30 долларов и поднимаются в свой номер. Носильщик приносит их сумки и возвращает им 5 долларов, потому что в отеле действует специальное предложение по будням. Трое друзей оставляют себе по одному доллару и дают носильщику 2 доллара чаевых. Позже они садятся, чтобы подсчитать свои расходы на выходные, и обнаруживают, что у них есть проблема.
Каждый из них заплатил по 10 долларов за комнату и получил по 1 доллару каждый, таким образом, их взносы составили 9 долларов. Затем они дали носильщику 2 доллара чаевых. Однако 9 умножить на три — это 27, плюс два — это 29 долларов. Куда делся лишний доллар?
Ответ:
Это немного запутанно, но все сводится к тому, что математика трех друзей неверна. Они не потратили 29 долларов, они потратили 27 долларов: 25 долларов на номер и 2 доллара на чаевые носильщику. Три оставшихся доллара им вернули!
Они не потратили 29 долларов, они потратили 27 долларов: 25 долларов на номер и 2 доллара на чаевые носильщику. Три оставшихся доллара им вернули!
СВЯЗАННЫЕ: Детективные загадки
Aaron Amat/Shutterstock
Сложные математические загадки: карточные игрыНебольшое количество карточек утеряно из полной колоды. Если я сдам четыре человека, останется три карты. Если я сдаю троим, остаются две, а если раздаю пятерым, остаются две карты. Сколько карт?
Ответ:
Это довольно сложно, но ответ таков: 47 карт. Чтобы получить ответ, нужно знать, что в колоде 52 карты. Затем найдите числа, кратные четырем, трем и пяти, ближайшие к этому числу, и посмотрите, совпадают ли какие-либо из них. Например, вы можете раздать 42, 44 и 48 карт четырем людям, что будет означать 9, 5 или 1 карты не хватает (осталось три). Однако единственный, который работает для кратных трем и пяти человек, — это когда не хватает пяти карт, что дает нам в общей сложности 47 карт.
СВЯЗАННЫЕ: Лучшие карточные игры для двух игроков
Мин К. Чиу/Shutterstock
Сложные математические загадки: ходы конемУ меня есть калькулятор, который может отображать десять цифр. Сколько различных десятизначных чисел я могу ввести, используя только цифры от 0 до 9?клавиши по одному разу и переход от одной клавиши к другой с помощью хода конем в шахматах? (В шахматах конь ходит в форме буквы L: одна клетка вверх и две поперек, две клетки вниз и одна поперек, две клетки вверх и одна поперек и другие подобные комбинации.)
Ответ:
Вы можете составить числа 5034927618 и 5038167294. Вы также можете составить их реверсы: 8167294305 и 4927618305. Следовательно, можно составить четыре разных числа. Ключевым моментом является понимание того, что номер должен начинаться или заканчиваться на клавише «5», за которой следует или предшествует клавиша «0», в противном случае невозможно использовать все десять клавиш во время маршрута.
СВЯЗАННЫЕ: Простые математические трюки
baona/Getty Images
Сложные математические загадки: Компания ТроихВы знаете, что 2 + 2 равно 2 x 2. Теперь найдите набор из трех различных целых чисел, сумма которых равна их общей сумме при умножении.
Ответ:
Три разных целых числа, сумма которых при умножении равна их сумме, это 1, 2 и 3. Нужны еще загадки? Посмотрите, сколько из этих библейских загадок вы сможете разгадать.
Catalin Petolea/Shutterstock
Сложные математические загадки: урожай яблок Миссис Джонс очень гордилась своей яблоней. Однажды осенью, собрав урожай яблок, она позвала троих своих сыновей. «Вот 150 яблок», — сказала она. — Я хочу, чтобы ты отнес их завтра на рынок и продал мне. Она дала Полу 15 яблок, Нику 50 и Бену 85. «Ваша задача, — добавила миссис Джонс, — продать яблоки таким образом, чтобы каждый из вас принес домой одинаковую сумму денег». Как они это делают?
Как они это делают?
Ответ:
Первый покупатель покупает 12 дюжин яблок по цене 1 доллар за дюжину. Пол продает ему дюжину, и у него остается три яблока; Ник продает ему четыре дюжины, и у него остается два яблока; и Бен продает ему семь дюжин, и у него остается одно яблоко. Затем приходит второй покупатель и покупает все оставшиеся у них яблоки по 3 доллара за штуку. Трое братьев отправляются домой с 10 долларами каждый.
СВЯЗАННЫЕ: Самая сложная головоломка
Ханасаки/Getty Images
Сложные математические загадки: Семь разКакое наименьшее целое число равно семикратной сумме своих цифр?
Ответ:
Ответ на эту математическую загадку равен 21. Вероятно, вы только что догадались ответить на эту математическую загадку, и это хорошо, но вы также можете решить ее алгебраически. Двузначное число ab означает 10a + b, так как первая цифра представляет десятки, а вторая — единицы. Если 10а + b = 7(а + b), то 10а + b = 7а + 7b и, следовательно, 3а = 6b, или, проще говоря, а = 2b. То есть вторая цифра должна быть в два раза больше первой. Наименьшее такое число — 21. Посмотрите эти головоломки, если вы действительно хотите потренировать свой мозг.
Если 10а + b = 7(а + b), то 10а + b = 7а + 7b и, следовательно, 3а = 6b, или, проще говоря, а = 2b. То есть вторая цифра должна быть в два раза больше первой. Наименьшее такое число — 21. Посмотрите эти головоломки, если вы действительно хотите потренировать свой мозг.
YamabikaY/Shutterstock
Сложные математические загадки: Деньги на обедДжон заметил, что сумма, которую он платил за свой обед, представляла собой перестановку цифр суммы денег, которая была у него в кармане, и что деньги, которые он имел, осталась еще одна перестановка тех же трех цифр! С какой суммы денег начал Джон?
Ответ:
Джон начал с $9,54. Деньги можно записать всего тремя цифрами, поэтому они должны быть от 1,01 до 9 долларов.0,99. Метод проб и ошибок показывает, что к этому вопросу подходит только один набор чисел: 9,54 доллара = 4,59 доллара + 4,95 доллара.
СВЯЗАННЫЕ: Загадка Эйнштейна
подземный мир/Shutterstock
Сложные математические загадки: числа в перевернутом видеКакое наименьшее число увеличится на 12, если его перевернуть и перевернуть?
Ответ:
Ответ: 86. Если его перевернуть и перевернуть, получится 98, что на 12 больше, чем 86.
Если его перевернуть и перевернуть, получится 98, что на 12 больше, чем 86.
ДАЛЕЕ: Длинные загадки
Первоначально опубликовано: 11 июня 2021 г.
Морган Кутоло
Морган является старшим производственным редактором Trusted Media Brands. В 2016 году она окончила Университет Нью-Гэмпшира, где получила степень бакалавра искусств в области журналистики. Она работает с нашими координаторами по производству, чтобы поддерживать движение контента и следить за тем, чтобы за кулисами все работало хорошо для всех наших цифровых сайтов. В свободное время ей нравится исследовать побережье штата Мэн, где она живет и работает удаленно полный рабочий день, а также уютно устроится на диване со своим корги Эгго, чтобы посмотреть HGTV или «Офис».
Сборник головоломок и головоломок Reader’s Digest . Авторские права ©2000 Reader’s Digest Association Far East Limited. Игры для мозга: веселые тренировки для острого ума . Copyright © Reader’s Digest Association Far East Limited 2015
Copyright © Reader’s Digest Association Far East Limited 2015
2.3: Писателями могут быть только гении
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 60936
- Шерил Э. Болл и Дрю М. Лоу изд.
- Университет Западной Вирджинии через Институт цифровых публикаций и библиотеки Университета Западной Вирджинии
Авторы: Дастин Эдвардс @edwardsdusty, Энрике Пас @eepaziii Университет Южного Иллинойса Карбондейл
Наша американская культура и образование культивируют довольно романтичную идею авторства. Преподавание словесности и литературы последовательно и часто сильно знакомит учащихся с писателями, которые были канонизированы как Великие: гении мысли, искусные мастера словесности и вдохновенные творцы — одним словом, авторы — которые превзошли человечество и смертность. Шекспир, Эмерсон, Оруэлл и так далее — это были настоящие писатели! — говорят они. Эти писатели сидели за огромными письменными столами из красного дерева в отдаленных хижинах, укрывшихся в самых тихих и безлюдных озерах и лесах. Эти писатели изолировали себя от всякого влияния и лихорадочно писали блестящие произведения, которые могли создать только их несравненные умы. Но эти писатели, какими бы великими они ни были, нанесли наибольший ущерб нашему нынешнему представлению о писательстве.
Шекспир, Эмерсон, Оруэлл и так далее — это были настоящие писатели! — говорят они. Эти писатели сидели за огромными письменными столами из красного дерева в отдаленных хижинах, укрывшихся в самых тихих и безлюдных озерах и лесах. Эти писатели изолировали себя от всякого влияния и лихорадочно писали блестящие произведения, которые могли создать только их несравненные умы. Но эти писатели, какими бы великими они ни были, нанесли наибольший ущерб нашему нынешнему представлению о писательстве.
Образ этого автономного, гениального и оригинального автора имеет большое значение; он обозначает желанный статус, с которым сравнивают многих, если не всех, писателей. Он запечатлен в дебатах об интеллектуальной собственности, вплетен в тревогу и неуверенность по поводу плагиата и неразрывно связан с экономикой письма. Хуже всего то, что она упорно отказывается умирать, несмотря на настойчивые попытки свергнуть ее господство над обучением грамоте и культурным производством.
Вес гения
Как выпускники американских учебных заведений, мы лично испытали (и продолжаем испытывать) ущерб, который этот миф нанес тем, кто пишет. Гениальные писатели были просвещенными, мудрыми и проницательными наблюдателями мира и человечества. Они писали правду, как только могли, и этот источник лился свободно и легко. Но это не то, как письмо работает для нас. Писать тяжело . Так много письменных заданий, которые мы встречаем, непроницаемы, укреплены со всех сторон
Гениальные писатели были просвещенными, мудрыми и проницательными наблюдателями мира и человечества. Они писали правду, как только могли, и этот источник лился свободно и легко. Но это не то, как письмо работает для нас. Писать тяжело . Так много письменных заданий, которые мы встречаем, непроницаемы, укреплены со всех сторон
высокими и стальными фальшбортами. Мы колотим и прижимаемся к этим стенам — но ничего. Наша работа часто буксует, останавливается на месте. Мы, очевидно, не можем быть настоящими авторами, верно? Это должно быть так просто. Почему просто не выходит? Эти нереалистичные ожидания не могут быть единственным способом быть автором.
Эти гениальные авторы вводят многих писателей в заблуждение. Их самые разрушительные последствия — это нереалистичные ожидания, которые они предъявляют к обычным писателям. Писатель и эксперт по плагиату Ребекка Мур Ховард считает, что представление об одиноком гениальном авторе увековечило атмосферу, в которой начинающие писатели боятся показаться неоригинальными и должны стремиться доказать свою креативность и гениальность. Достаточно взглянуть на фирменный язык службы обнаружения плагиата Turnitin, самопровозглашенной «проверки оригинальности», чтобы увидеть, как это проявляется в реальных сценариях. Требование оригинальности разочаровывает многих писателей, которые не понимают, как у них может быть гениальность, чтобы открыть оригинальную мысль.
Достаточно взглянуть на фирменный язык службы обнаружения плагиата Turnitin, самопровозглашенной «проверки оригинальности», чтобы увидеть, как это проявляется в реальных сценариях. Требование оригинальности разочаровывает многих писателей, которые не понимают, как у них может быть гениальность, чтобы открыть оригинальную мысль.
Другие писатели, работающие как в академической среде, так и за ее пределами, испытывают аналогичные трудности, когда чувствуют, что их писательский процесс не соответствует прославленному образу Великих. В коротком эссе The Irish Times писатель и музыкант Джош Риттер пишет о том, как он боролся с имиджем гениальных авторов. Он никогда не чувствовал, что его сочинение песен считается настоящим сочинением, что может произойти только с великими секреторами, написанными пером и чернилами и закрепленными на пергаменте. Он пишет: «Неважно, что всю свою писательскую жизнь я писал за кухонным столом, с гитарой на коленях, с ручкой и блокнотом под рукой, если бы я хотел стать настоящим писателем, мне нужен был бы письменный стол. […] А без письменного стола как бы я мог написать свой роман?» Риттер обнаруживает, что его ограничивает образ письма и писателей, который представляет письменный стол. Без письменного стола Риттер не может представить, что у него есть способность написать достойное произведение, точно так же, как многие не чувствуют себя настоящими писателями, если они борются и стараются, когда пишут. Но Риттер приходит к выводу, который разделяем и мы: отдаленные хижины вдоль изолированных озер, огромные письменные столы, вырезанные из кедров, блестящие рукописи, рожденные за один присест при свечах, — все это не совсем точно отражает то, на что похоже письмо для кого-либо.
[…] А без письменного стола как бы я мог написать свой роман?» Риттер обнаруживает, что его ограничивает образ письма и писателей, который представляет письменный стол. Без письменного стола Риттер не может представить, что у него есть способность написать достойное произведение, точно так же, как многие не чувствуют себя настоящими писателями, если они борются и стараются, когда пишут. Но Риттер приходит к выводу, который разделяем и мы: отдаленные хижины вдоль изолированных озер, огромные письменные столы, вырезанные из кедров, блестящие рукописи, рожденные за один присест при свечах, — все это не совсем точно отражает то, на что похоже письмо для кого-либо.
Между белоснежными страницами и искусно написанными словами хорошо спрятан тот же процесс испытаний, через который многие проходят каждый раз, когда они открывают документ или держат ручку, а также те же непреклонные баррикады, которые не дают им пройти, которые часто уступают место только тогда, когда они находятся под влиянием и вдохновляются другими. Сказки гениальных писателей, которые изливают идеально структурированную прозу на свои собственные, рассказывают небылицы, а не реальность. (См. главу Тери Холбрук и Мелани Хандли в другом месте этой книги, чтобы узнать больше о плохих мифах о писателях.) Наоборот, эти писатели, безусловно, были очень похожи на нас — нервными, разочарованными, измученными и уставшими, ищущими помощи в 1:38 ночи. пытаемся уложиться в срок. Та помощь, которую мы действительно находим, редко исходит от гениальных, своевольных прозрений. Вместо этого мы находим утешение, поддержку и успех, когда смотрим вовне, заимствуем идеи, делаем ремиксы на другие тексты, разговариваем с другими и сотрудничаем с их мыслями. Автора Одинокого гения не существует. И никогда не было.
Сказки гениальных писателей, которые изливают идеально структурированную прозу на свои собственные, рассказывают небылицы, а не реальность. (См. главу Тери Холбрук и Мелани Хандли в другом месте этой книги, чтобы узнать больше о плохих мифах о писателях.) Наоборот, эти писатели, безусловно, были очень похожи на нас — нервными, разочарованными, измученными и уставшими, ищущими помощи в 1:38 ночи. пытаемся уложиться в срок. Та помощь, которую мы действительно находим, редко исходит от гениальных, своевольных прозрений. Вместо этого мы находим утешение, поддержку и успех, когда смотрим вовне, заимствуем идеи, делаем ремиксы на другие тексты, разговариваем с другими и сотрудничаем с их мыслями. Автора Одинокого гения не существует. И никогда не было.
Тем не менее, такое понимание авторства стало настолько обыденным, настолько натурализованным, что немногие когда-либо задавались вопросом о его происхождении. Более пристальный взгляд на этот миф показывает, что автор был выкован совсем недавно в западной истории. По словам историка литературы Марты Вудманси, изобретение автора в его нынешнем виде восходит к Европе I века. Именно в этом столетии, согласно анализу Вудманси, начался более масштабный культурный сдвиг, и из водоворота изменений — технологических, правовых, экономических и культурных — начало появляться новое определение современного автора. Это автор, который в значительной степени придерживается сегодня: создатель, владелец и владелец уникальных, оригинальных произведений, таких как эссе, книги, стихи и так далее.
По словам историка литературы Марты Вудманси, изобретение автора в его нынешнем виде восходит к Европе I века. Именно в этом столетии, согласно анализу Вудманси, начался более масштабный культурный сдвиг, и из водоворота изменений — технологических, правовых, экономических и культурных — начало появляться новое определение современного автора. Это автор, который в значительной степени придерживается сегодня: создатель, владелец и владелец уникальных, оригинальных произведений, таких как эссе, книги, стихи и так далее.
Изобретение гения
Взгляды на письмо, ведущие к современным идеалам об авторах, развивались вместе с распространением популярных трактатов об оригинальности. В 1759 году, например, влиятельный писатель и поэт Эдвард Юнг «Предположения об оригинальной композиции» начал проводить глубокие различия между оригинальным и подражательным авторством. Оригинальность, утверждал Янг, естественным образом проистекает из врожденного корня гениальности, как растение, приносящее плоды. Имитации, с другой стороны, были искусственными низшими, созданными из работы других. Эссе Янга и многие другие, подобные ему, начали принудительно перенаправлять источник вдохновения. Они утверждали, что настоящие авторы не вдохновляются внешним миром; они вдохновлены своей уникальной сущностью. Настоящие авторы не подражатели; они создатели. Настоящими авторами не становятся; они рождаются.
Имитации, с другой стороны, были искусственными низшими, созданными из работы других. Эссе Янга и многие другие, подобные ему, начали принудительно перенаправлять источник вдохновения. Они утверждали, что настоящие авторы не вдохновляются внешним миром; они вдохновлены своей уникальной сущностью. Настоящие авторы не подражатели; они создатели. Настоящими авторами не становятся; они рождаются.
Это перенаправление вдохновения также совпало с рождением нового класса писателей: профессиональных авторов. Теперь эссеисты, поэты и другие представители общественной интеллигенции заявляли о себе, что письмо было их основным средством заработка на жизнь. Во многом благодаря расширению круга читателей благодаря достижениям в технологии печати
возникла потребность найти способы для профессиональных писателей (и издательской индустрии) зарабатывать деньги на своих печатных произведениях. Введите авторские права. Ранние законы об авторском праве, согласно анализу авторского права историка Марка Роуза, помогли сформировать понимание автора как владельца и владельца его или ее индивидуальных идей. Другими словами, авторское право помогло определить автора как автора: автономного человека, оригинальные идеи которого заслуживают правовой защиты и денежного вознаграждения.
Другими словами, авторское право помогло определить автора как автора: автономного человека, оригинальные идеи которого заслуживают правовой защиты и денежного вознаграждения.
Есть много причин, по которым такое понимание автора сохраняется и сегодня. Принципы оригинальности, собственности, права собственности и гениальности прочно вошли в ткань западного авторства. Гениальное авторство закодировано в наших правовых и экономических системах и поддерживается годами обучения. Наше понимание автора также является продуктом самой издательской индустрии. Издатели представляют отполированную и доработанную копию текста и тем самым разбавляют беспорядок процесса написания. Идею о том, что авторы черпают свои писательские способности из своего природного интеллекта, трудно поколебать, потому что она вписана в само слово 9.0290 автор сама.
Но так было не всегда. Более глубокий взгляд на историю вместе с сегодняшними методами цифрового письма показывает, как можно бросить вызов мифу об одиноком оригинальном гении. В частности, альтернативы гениальности видят ценность в подражании, сотрудничестве и ремиксах. Авторы не действуют изолированно, а оказываются в окружении других идей, людей и текстов.
В частности, альтернативы гениальности видят ценность в подражании, сотрудничестве и ремиксах. Авторы не действуют изолированно, а оказываются в окружении других идей, людей и текстов.
Альтернатива гениальности
До того, как идея гениального авторства утвердилась, Вудманси отмечает, что авторов обычно изображали либо как носителей (получающих идеи из какого-то внешнего источника), либо как мастеров (изготовляющих новые материалы из множества разрозненных источников). Еще более глубокая история обнаруживает более почитаемое отношение к подражанию. Практика подражания — черпать вдохновение из внешних источников путем заимствования, адаптации и изменения моделей из богатого запаса источников — в значительной степени ценилась в древних культурах. Подражание — это то, как студенты обучались своему ремеслу, и это рассматривалось как способ изобретать новые значения из существующих материалов. Фактически, древние философы и поэты часто использовали метафору преобразующей пчелы для описания работы подражания. Как писал Сенека в IV веке до н. э., «люди говорят, что мы должны следовать примеру пчел, которые порхают и собирают цветы, пригодные для производства меда, а затем раскладывают и сортируют в своих ячейках все, что они принесли. в.» Эта метафора предполагает, что акт создания новой работы включает в себя сбор кусочков из множества различных внешних источников.
Как писал Сенека в IV веке до н. э., «люди говорят, что мы должны следовать примеру пчел, которые порхают и собирают цветы, пригодные для производства меда, а затем раскладывают и сортируют в своих ячейках все, что они принесли. в.» Эта метафора предполагает, что акт создания новой работы включает в себя сбор кусочков из множества различных внешних источников.
Эти исторические практики и идеи об авторстве демонстрируют, чем когда-то было письмо и чем, по нашему мнению, оно должно быть: совместными усилиями в постоянном и глубоком обсуждении работ и идей других. Другими словами, вместо гениев-затворников мы стремимся стать социальными писателями. Вместо вдохновения изнутри мы ищем влияния извне. Чтобы писать, нужно разговаривать с друзьями, просить помощи у коллег, находить ответы и идеи в чужих трудах и заниматься этим. Мы предпочитаем сотрудничество, а не изоляцию, и именно эту модель письма мы утверждаем, что образование должно продвигать писателей и студентов во всем мире.
В каком-то смысле странно призывать к большему совместному творчеству или написанию под влиянием других, потому что это уже происходит повсюду. Многие ученые подтверждают, что сотрудничество, а не изоляция, является доминирующим подходом к повседневному сочинению. Исследователи письма Лиза Эде и Андреа Лансфорд, например, изучали работы писателей в различных областях, включая инженерное дело, психологию, химию и даже санитарию. Они обнаруживают, что профессионалы в этих областях в значительной степени полагаются на сотрудничество, чтобы добиться успеха в своих письменных задачах. Точно так же писатель-исследователь Джоан Маллин подтверждает, что многие художники — живописцы, архитекторы, дизайнеры одежды, графики и многие другие — всегда чувствуют, что их работа является совместной, и часто учатся, подражая, подражая и даже копируя работы других. Эти писатели и художники в значительной степени полагаются на мысли и идеи других, которые помогают им учиться и добиваться успеха, и их успех показывает, почему это должно быть стандартным подходом ко всему письму.
Многие ученые подтверждают, что сотрудничество, а не изоляция, является доминирующим подходом к повседневному сочинению. Исследователи письма Лиза Эде и Андреа Лансфорд, например, изучали работы писателей в различных областях, включая инженерное дело, психологию, химию и даже санитарию. Они обнаруживают, что профессионалы в этих областях в значительной степени полагаются на сотрудничество, чтобы добиться успеха в своих письменных задачах. Точно так же писатель-исследователь Джоан Маллин подтверждает, что многие художники — живописцы, архитекторы, дизайнеры одежды, графики и многие другие — всегда чувствуют, что их работа является совместной, и часто учатся, подражая, подражая и даже копируя работы других. Эти писатели и художники в значительной степени полагаются на мысли и идеи других, которые помогают им учиться и добиваться успеха, и их успех показывает, почему это должно быть стандартным подходом ко всему письму.
Более того, совместная работа включает в себя больше, чем акт письма с другими теплыми телами в комнате. Это также предполагает другой вид сотрудничества: повторное использование, переработку и перепрофилирование существующих материалов для новых целей. В наш цифровой век обычные люди все чаще имеют доступ к обширным хранилищам архивных материалов. Примечательно, что эти материалы можно использовать для новых целей. Специалисты по риторике Джим Ридольфо и Даниэль Николь ДеВосс называют этот процесс создания ремикса «взятием старых фрагментов текста, изображений, звуков и видео и объединением их вместе для создания нового продукта». Письмо, если рассматривать его таким образом, не основано на ценностях изоляции, внутреннего вдохновения или оригинальности; скорее, он видит ценность в совместном использовании, явном влиянии и обновлении. Возможно, удивительно, как отмечает исследователь СМИ Генри Дженкинс, язык ремиксов оживляет
Это также предполагает другой вид сотрудничества: повторное использование, переработку и перепрофилирование существующих материалов для новых целей. В наш цифровой век обычные люди все чаще имеют доступ к обширным хранилищам архивных материалов. Примечательно, что эти материалы можно использовать для новых целей. Специалисты по риторике Джим Ридольфо и Даниэль Николь ДеВосс называют этот процесс создания ремикса «взятием старых фрагментов текста, изображений, звуков и видео и объединением их вместе для создания нового продукта». Письмо, если рассматривать его таким образом, не основано на ценностях изоляции, внутреннего вдохновения или оригинальности; скорее, он видит ценность в совместном использовании, явном влиянии и обновлении. Возможно, удивительно, как отмечает исследователь СМИ Генри Дженкинс, язык ремиксов оживляет
более старые, доромантические идеалы авторства. Поворот к ремиксам и заимствованиям для Дженкинса «не так радикален, если рассматривать его на более широком фоне человеческой истории», несмотря на глубоко укоренившийся идеал творческого гения, пропагандируемый в новейшей истории.
Как показывает история и современная практика, писательство всегда требовало глубокого общественного участия и влияния, и ни один писатель не добился успеха исключительно благодаря сверхъестественному интеллекту или таланту. Всепроникающая идея автора-затворника и гения, рождающего прозу, свободную от влияния, должна умереть, и вслед за ней расцветет обновленная идея продуктивного и значимого сотрудничества (с другими писателями и их текстами).
Дополнительная литература
Чтобы узнать больше о том, как на самом деле сочиняют современные писатели, рассмотрите книгу Лизы Эде и Андреа Лансфорд Тексты в единственном числе/множественное число авторов : Перспективы совместного письма (издательство Южного Иллинойского университета), Кэрол Петерсен Хэвиленд и Джоан А. Маллина, кому принадлежит этот текст ?: Плагиат, авторство и дисциплинарные культуры (издательство государственного университета штата Юта), Майори Перлофф, неоригинальный гений: поэзия другими средствами в новом веке (издательство Чикагского университета) и Кевина Голдсмита «Нетворческое письмо: управление языком в эпоху цифровых технологий» (издательство Колумбийского университета). Кроме того, статья Джоша Риттера «Риттер в мягкой обложке» — это его рассказ о том, как на него лично повлияли мифы об авторстве, когда он писал свою книгу .
Кроме того, статья Джоша Риттера «Риттер в мягкой обложке» — это его рассказ о том, как на него лично повлияли мифы об авторстве, когда он писал свою книгу .
Для получения дополнительной информации о ремиксах см. Ремикс Лоуренса Лессига: Обеспечение процветания искусства и коммерции в гибридной экономике (Penguin Press), Джим Ридольфо и Даниэль Николь ДеВосс «Сочинение для рекомпозиции: риторическая скорость и подача», веб-сайт Кирби Фергюсона. серия Everything is a Remix и статья Джонатана Летема «Экстаз влияния: плагиат» в Harper’s Magazine .
Разговоры об оригинальности часто пересекаются с вопросами о плагиате. Чтобы подробнее изучить эту связь, см. книгу Ребекки Мур Ховард «В тени гигантов: плагиаторы, авторы и сотрудничество» (Ablex), книгу Сьюзан Блюм «Мое слово!». Плагиат и культура колледжей (Cornell University Press) и Николуса Кулиша New York Times статья о книге-бестселлере автора Хелен Хегеманн, вызвавшей споры из-за плагиата.
Чтобы узнать больше об истории и теории авторства, обратитесь к статье Эндрю Галлакса «В теории: смерть автора», книге Марка Роуза « авторов и владельцев: изобретение авторского права » (издательство Гарвардского университета) и статье Марты Вудманси. «Гений и
Копирайт: экономико-правовые условия возникновения «автора»» ( Исследования восемнадцатого века ).
Ключевые слова
авторство, сотрудничество, гениальность, история авторства, влияние, оригинальность, ремикс
Биография автора
Исследования Дастина Эдвардса сосредоточены на написании в цифровой среде, интеллектуальной собственности и изучении авторства. Он писал о том, как письмо для внеклассных, профессиональных и гражданских целей может — и должно — повлиять на преподавание письма в университетских условиях. С ним можно связаться в Твиттере @edwardsdusty.
Энрике Паз изучает авторство и плагиат и преподает письмо. Его интересует, как люди начинают видеть себя писателями или авторами. Работая со многими другими писателями, он опубликовал эссе о том, как писатели могут эффективно сотрудничать и, в частности, о том, как преподаватели и студенты могут и должны сотрудничать, чтобы способствовать обучению и успеху. Вы можете найти его в Твиттере @eepaziii.
Работая со многими другими писателями, он опубликовал эссе о том, как писатели могут эффективно сотрудничать и, в частности, о том, как преподаватели и студенты могут и должны сотрудничать, чтобы способствовать обучению и успеху. Вы можете найти его в Твиттере @eepaziii.
Эта страница под названием 2.3: Писателями могут быть только гении, опубликована под лицензией CC BY, автором, ремиксом и/или куратором выступили Шерил Э. Болл и Дрю М. Лоу, изд. (Институт цифровых публикаций и библиотеки Университета Западной Вирджинии).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Шерил Э.


 Если вы считаете себя меломаном и при этом хорошо знаете всех знаковых […] Больше
Если вы считаете себя меломаном и при этом хорошо знаете всех знаковых […] Больше Любимые булочки, хлеб и макароны нет так уж безобидны. В их состав входит […] Больше
Любимые булочки, хлеб и макароны нет так уж безобидны. В их состав входит […] Больше